Facteur d'emballage

Le facteur d'emballage est une fraction qui indique le volume que les particules occupent, que ce soit des atomes, des ions ou des molécules, dans l'espace interne d'un cristal. Sa valeur est toujours inférieure à 1, ce qui devient 100% du volume du verre; Plus exactement, sa cellule unitaire, qui est la plus petite représentation de tout le verre.

Un facteur d'emballage de 100% signifie que les particules occupent le volume de la cellule unitaire dans son intégralité. Physiquement, il est impossible que cela se produise, car cela impliquerait, par exemple, que les atomes déforment leurs radios et se dissoudraient comme s'ils étaient un "liquide électronique". La géométrie des atomes, sphérique pour la commodité, se traduit toujours par des espaces vides pendant l'emballage.

Comme cela se produit dans les machines de distribution sucrées, le facteur d'emballage nous dit à quel point les particules de cristal sont «serrées»: plus elle est grande, plus

Dans la définition du facteur d'emballage, il est supposé que les atomes sont constitués de sphères rigides, telles que des boules de gomme ou de bonbons d'une machine distribuée (image supérieure). Parmi les sphères, il y aura toujours des espaces creux où des sphères plus petites (impuretés ou additifs peuvent être glissées).

Si nous augmentons le facteur d'emballage, les sphères seront pressées, tournant le verre le plus compact et le plus dense; ou d'un autre côté, plus déformable, comme avec les métaux malléables et ductils.

Le facteur d'emballage s'applique à tout type de verre. Cependant, son calcul peut devenir un peu fastidieux, il ne sera donc considéré que pour les cristaux atomiques avec des structures simples.

[TOC]

Formule de facteur d'emballage

Le facteur d'emballage est généralement exprimé en pourcentages. Par exemple, si sa valeur est de 40%, cela signifie que les particules occupent à peine 40% de l'espace total de la cellule unitaire; Ou ce qui est la même chose que de dire que 60% du verre est "vide".

Ce qui précède clarifie quelle est la formule pour calculer ce facteur:

• Ugly = (volume d'atomes) / (volume de cellules unitaires)

Où le laid signifie Facteur d'emballage atomique, Quels sont les cristaux les plus simples.

Le volume de la cellule unitaire dépend de ses paramètres (comme la longueur de ses côtés), avec lesquels il se déroule par simple géométrie pour calculer son volume. Les atomes, en revanche, sont ceux qui définissent la cellule, il est donc possible d'exprimer les dimensions de la même chose à partir des radios atomiques, comme on le verra dans les sections suivantes.

Il peut vous servir: mélange racémique: chiralité, exemples

En ce qui concerne le volume d'atomes, le nombre total d'entre eux qui est présent dans la cellule unitaire (1, 2, 3, etc.), ainsi que sa géométrie sphérique. Par conséquent, la formule est un peu modifiée:

Ugly = (nº atomes) (volume d'atomes) / (volume de cellules unitaires)

Pour calculer laid, vous devez déterminer alors Non., V_atome et V_{Cellule unitaire}.

Simple cube

Cellule d'unité cubique simple. Source: CCC_CRYSTAL_CELL_ (OPAQUE).SVG: * Cobique_Cente_Atomes_Par_MILLE.SVG: CDANG (Idée originale et exécution SVG), Samuel Dupré (Odeeling 3D avec SolidWorks) Dérive Work: Daniele Pugliesi (Talk) Derive Work: Daniele Pugliesi, CC BY-SA 3.0, via Wikimedia Commons

La cellule unitaire la plus simple de tous est le simple cube. Nous y avons quelques parties d'atomes dans chacun des coins. Si nous voyons, nous remarquerons que la longueur pour De cette cellule, il est égal à 2R, car ce sont les atomes qui définissent la cellule. Ainsi, le volume de la cellule unitaire sera égal à:

V_{Cellule unitaire} = pour³ (volume d'un cube)

= (2r)³

= 8r³

En attendant, le volume de l'atome sera égal à:

V_atome = (4/3) πr³ (volume d'une sphère)

Chacun des coins est partagé par 8 autres cellules unitaires voisines. Par conséquent, nous avons une fraction 1/8 dans chaque coin, et en ayant 8 d'entre eux, nous ne nous soucions pas de 1 atome par cellule unitaire (1/8 x 8 = 1).

Le facteur d'emballage est:

Moche = (1) (4/3) πr³ / 8r³

= π / 6 ≈ 52%

C'est-à-dire dans une simple cellule cubique, les atomes occupent 52% de l'ensemble du volume de verre.

Centré cubes dans le corps

Détermination du volume cellulaire

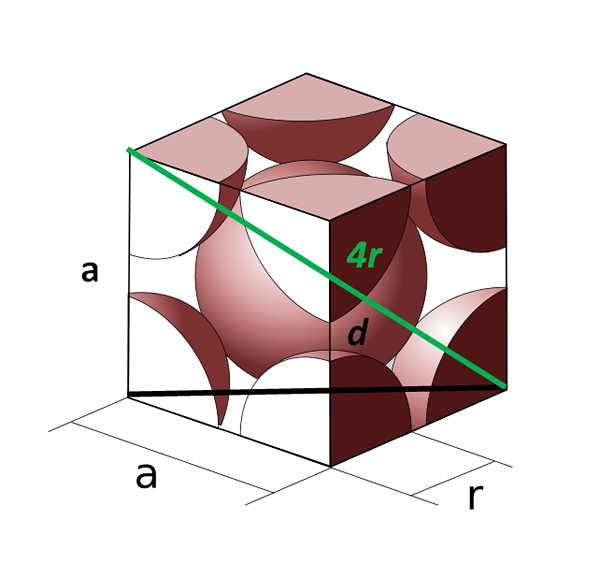Corps unitaire cellulaire centrée sur le corps. Source: Cobique_Centre_Atomes_Par_Maitle.SVG: CDANG (Idée originale et exécution SVG), Samuel Dupré (3D Odeeling with SolidWorks) Travail dérivé: Daniele Pugliesi, CC BY-SA 3.0, via Wikimedia Commons

Voyons maintenant la cellule cubique centrée sur le corps. Le côté pour Il ne peut plus être égal à 2R, car nous avons un espace vide entre les deux atomes des coins. Il y a donc une diagonale d égal à 4r (couleur verte) qui traverse la cellule à travers le centre et touche les coins opposés, et une autre diagonale d du visage (noir).

Les cotés pour, d et 4r dessinez un triangle rectangle auquel nous pouvons appliquer la trigonométrie pour calculer quelle est la valeur de pour:

(4r)² = D² + pour²

Peut vous servir: forces intermoléculaires

Mais d'un autre côté, à la base de la cellule unitaire, nous avons un autre triangle (pour, pour et d) auquel nous pouvons calculer l'hypoténuse:

d²  = A² + pour²

= 2A²

Remplacement alors nous aurons:

(4r)² = (2e²) + a²

(4r)² = 3A²

A = (4 / √3) r

Le V_{Cellule unitaire} est égal à:

V_{Cellule unitaire} = A³

= ((4 / √3) r)³

Détermination du facteur d'emballage

Notez qu'en ce qui concerne le nombre d'atomes, nous avons 1 atome à l'intérieur de cette cellule, après la même déduction faite pour la simple cellule cubique, et un autre atome supplémentaire situé au centre de la cellule. Ainsi, il y a un total de 2 atomes pour chaque cellule cubique centrée sur le corps.

Le facteur d'emballage est alors:

Moche = (2) (4/3) πr³ / ((4 / √3) r)³

= (√3 / 8) π ≈ 68%

Autrement dit, dans une cellule cubique axée sur le corps, 68% du volume de verre est occupé par des atomes. Par conséquent, cette arrangement cristallin est plus compact (ou dense) que le simple cube.

Coube centré sur les visages

Détermination du volume cellulaire

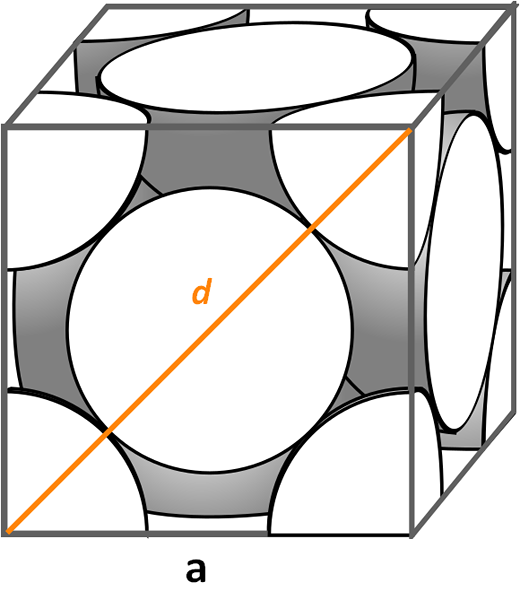Cellule unitaire cubique centrée sur les visages. Source: cdang, cc by-sa 3.0, via Wikimedia Commons

Regardons la cellule unitaire cubique centrée sur les visages, très courante dans les symphines de sels inorganiques et certains métaux, comme l'or et l'argent. Pour déterminer son facteur d'emballage, nous devons commencer, en suivant les exemples précédents, pour trouver quel est le volume de sa cellule unitaire. Il est nécessaire de calculer à nouveau le côté pour Et donc le volume du cube pour³.

Cette fois, la procédure est plus facile et plus directe, car nous avons une diagonale d Avant cela, avec les côtés pour, Ils forment un triangle droit auquel nous pouvons appliquer la trigonométrie:

d² = A² + pour²

= 2A²

Clairière pour nous aurons:

pour = D / √2

Mais, nous remarquons visuellement que d Il est égal à 4R, nous faisons donc une substitution:

pour = 4r / √2

= 2r 2^{1-1 / 2}

= (2√2) R

Être V_{Cellule unitaire} égal à:

pour³ = ((2√2) r)³

= (16√2) R³

En ce qui concerne le nombre d'atomes par cellule, nous avons huit parties d'un atome dans chaque coin, et aussi la moitié d'atome pour chacun des six faces, qui est partagée par une autre cellule voisine. Par conséquent, le nombre d'atomes est égal à:

Nº atomes = 1/8 (8) + 1/2 (6) = 1 + 3 = 4

Détermination du facteur d'emballage

Avoir cela, il y a 4 atomes dans chaque cellule cubique axée sur les visages, ainsi que son volume, qui est égal à (16√2) R³, Nous pouvons ensuite calculer le facteur d'emballage:

Ugly = (nº atomes) (volume d'atomes) / (volume de cellules unitaires)

= (4) (4/3) πr³ / (16√2) r³

Il peut vous servir: groupe ACILO: structure, caractéristiques, composés et dérivés

= π / (3√2) ≈ 74%

Notez que cette cellule est encore plus compacte que les précédentes: 74% du volume total de la cellule est occupé par des atomes. Dans un cristal parfait et pur, cela équivaudrait à dire que 26% de son volume est disponible pour héberger d'autres atomes invités.

Hexagonal compact

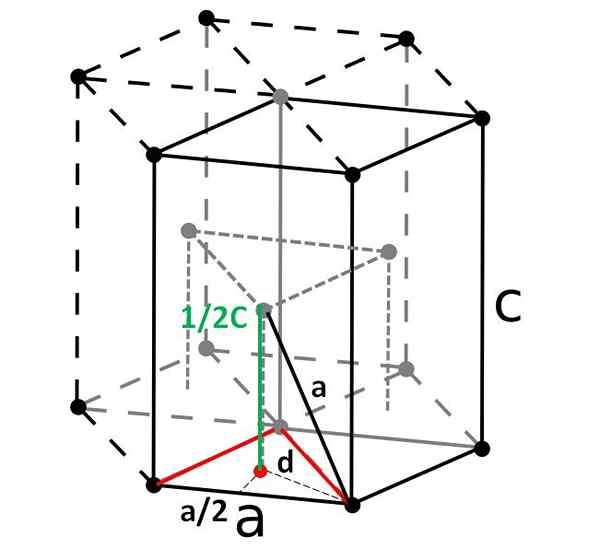Cellule hexagonale compacte et sa cellule primitive rhomboédrique. Source: Original: DornelfVector: DePiep, CC BY-SA 3.0, via Wikimedia Commons

Enfin, parmi les cellules unitaires les plus simples et les plus compactes, nous avons l'hexagonal compact. Contrairement aux précédents, le calcul de son volume est un peu plus lourd. Comme on peut le voir, il n'est pas cubique, il a donc deux paramètres pour et c, Ce dernier étant la hauteur de la cellule.

Détermination de la hauteur de la cellule

La cellule hexagonale peut être décomposée en trois cellules rhomboyens, et de l'une d'elles sera calculée pour et c. Le côté pour, Bien qu'il ne soit pas aussi évident dans l'image ci-dessus, elle est égale à 2r. Calculer c, Au lieu de cela, nous utilisons le triangle et le produit Red Point du prisme triangulaire interne de la même cellule.

Nous devons calculer la distance d Pour pouvoir déterminer combien il vaut c. Sur le sol, le triangle rouge est équilatéral, avec un angle de 60º. Mais si un autre triangle rectangulaire interne est considéré avec les côtés pour/ 2 et d, et un angle de 30º (moitié), puis par trigonométrie, nous pouvons déterminer d:

Cos (30º) = (pour/ 2) / d

d = pour/ √3

Et maintenant nous considérons le triangle droit composé des côtés c/ 2 (vert), pour (noir et d (pointé):

pour² = (pour/ √3)² + (C / 2)²

Clairière c Nous aurions:

c = √ (8/3) pour

Et remplacer pour Par 2r:

c = √ (8/3) (2R)

= √ (4 · 2/3) (2r)

= 4√ (2/3) R

Détermination du volume cellulaire

Pour déterminer le volume de la cellule hexagonale, vous devez multiplier la zone hexagonale par sa hauteur. Sachant que les triangles équilatéraux ont des côtés pour, Sa hauteur est calculée H. Ainsi, trouver la zone d'un triangle, qui est pour ce cas √3 / 4pour², Nous multiplions cette valeur par 6 pour obtenir la zone hexagone: 3 (√3 / 2)pour²

Le volume est donc:

V_{Cellule unitaire} = Zone hexagone x hauteur

= 3 (√3 / 2)pour² X 4√ (2/3) R

Et remplacer à nouveau pour Par 2r:

V_{Cellule unitaire}  = 3 (√3 / 2) (2r)² X 4√ (2/3) R

= 24√2 r³

Détermination du facteur d'emballage

Dans la cellule hexagonale, il y a 12 atomes dans les coins, qui ont 1/6 de leurs volumes à l'intérieur. Il y a aussi 3 atomes internes dont les volumes sont complets, et 2 autres atomes sur les faces supérieures et inférieures dont la moitié de ses volumes se trouvent à l'intérieur de la cellule.

Par conséquent, le nombre d'atomes est égal à:

Nº atome = 1/6 (12) + 1 (3) + 1/2 (2) = 6 atomes

Et le facteur d'emballage est enfin:

Ugly = (nº atomes) (volume d'atomes) / (volume de cellules unitaires)

= (6) (4/3) πr³ / 24√2 r³

= π / (3√2) ≈ 74%

Notez que le facteur de compartiment de la cellule hexagonale est le même que pour la cellule cubique centrée sur les faces. C'est-à-dire que les deux sont tout aussi compacts.

Les références

1. C. Barry Carter & M. GRANT NORTON. (2007). Science et ingénierie des matériaux en céramique. Springer.
2. Fhiver & Atkins. (2008). Chimie inorganique. (Quatrième édition). Mc Graw Hill.
3. Whitten, Davis, Peck & Stanley. (2008). Chimie. (8e Ed.). Cengage Learning.
4. Wikipédia. (2021). Facteur d'emballage atomique. Récupéré de: dans.Wikipédia.org
5. Brandon. (2021). Quel est le facteur d'emballage atomique (et comment le calculer pour SC, BCC, FCC et HCP)? Étudiant en sciences et en ingénierie des matériaux. Récupéré de: mSestudent.com