Y a-t-il des triangles scalène avec un angle droit?

Il existe de nombreux triangles de scalle avec un angle droit. Avant d'avancer sur le sujet, il est d'abord nécessaire de connaître les différents types de triangles qui existent. Les triangles sont classés par deux classes qui sont: leurs angles internes et les longueurs de leurs côtés.

La somme des angles internes de tout triangle est toujours égal à 180º. Mais selon les angles internes, les mesures sont classées comme:

-Acutangle: Ces triangles sont tels que leurs trois angles sont aigus, c'est-à-dire qu'ils mesurent moins de 90 ° chacun.

-Rectangle: Ce sont ces triangles qui ont un angle droit, c'est-à-dire un angle qui mesure 90 °, et, par conséquent, les deux autres angles sont aigus.

-Obtus: Ce sont les triangles qui ont un angle obtus, c'est-à-dire un angle dont la mesure est supérieure à 90 °.

Triangles Scalan avec un angle droit

L'intérêt pour cette partie est de déterminer si un triangle scalène peut avoir un angle droit.

Comme dit ci-dessus, un angle droit est un angle dont la mesure est de 90º. Il est seulement nécessaire de connaître la définition d'un triangle scalène, qui dépend de la longueur des côtés d'un triangle.

Classification des triangles selon leurs côtés

Selon la longueur de leurs côtés, les triangles sont classés comme:

-Équilatéral: Ce sont tous ces triangles tels que les longueurs de leurs trois côtés sont les mêmes.

-Isocèle: Ce sont les triangles qui ont exactement deux côtés de longueur égale.

-Scalène: Ce sont ces triangles sur lesquels les trois côtés ont des mesures différentes.

Formulation d'une question équivalente

Une question équivalente à celle du titre est «Y a-t-il des triangles qui ont les trois côtés avec des mesures différentes et cela a un angle de 90 °?"

La réponse comme indiqué au début est oui. Il n'est pas très difficile de justifier cette réponse.

S'il est soigneusement observé, aucun triangle rectangulaire n'est équilatéral, cela peut être justifié grâce au théorème de Pythagore pour les triangles rectangulaires, qui dit:

Étant donné un triangle rectangulaire que les longueurs de leurs catégories sont "A" et "B", et la longueur de son hypoténuse est "C", vous devez c² = a² + b², qui peut être vu que la longueur de l'hypoténuse " C "est toujours supérieur à la longueur de chaque jambe.

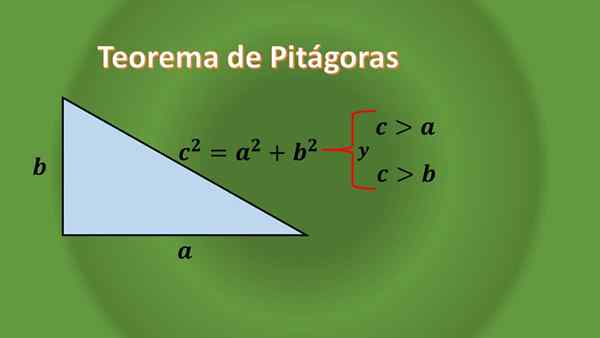
Comme rien n'est dit à propos de "A" et "B", cela implique qu'un triangle droit peut être isocèle ou scalène.

Ensuite, choisissez simplement n'importe quel triangle rectangle tel que ses jambes ont des mesures différentes, et donc un triangle scalène qui a un angle droit aura été choisi.

Exemples

-Si un triangle rectangulaire est considéré comme les jambes a respectivement 3 et 4, alors par le théorème de Pythagore, on peut conclure que l'hypoténuse aura une longueur de 5. Cela implique que le triangle est scalène et a un angle droit.

-Soit ABC un triangle rectangulaire avec des mesures des mesures 1 et 2. Alors la longueur de son hypoténuse est √5, ce qui conclut qu'ABC est un triangle rectangulaire scalène.

Tous les triangles d'échelle n'ont pas un angle droit. Vous pouvez considérer un triangle comme celui de la figure suivante, qui est scalène, mais aucun de ses angles internes n'est droit.

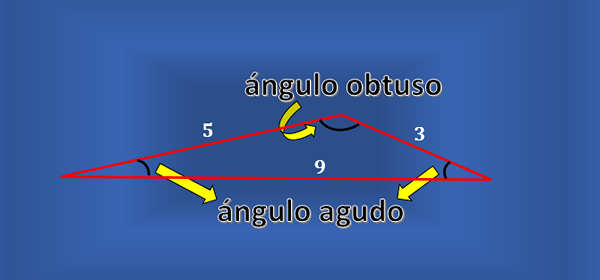De plus, tous les triangles droits ne sont pas scalène. Si vous considérez un triangle droit dont les jambes mesurent les deux 1, alors l'hypoténuse aura une mesure de √2. Par conséquent, le triangle rectangle est isoscèle.