Évaluation des fonctions

Pour évaluer une fonction dont le diagramme est connu, pour une certaine valeur ou élément de l'ensemble de départ, il suffit d'observer l'élément correspondant dans l'ensemble d'arrivée. Source: F. Zapata.

Quelle est l'évaluation des fonctions?

La Évaluation des fonctions Il consiste à déterminer l'image d'une certaine valeur de domaine. En d'autres termes, pour une valeur donnée de l'ensemble de départ, vous devez trouver son correspondant dans l'ensemble d'arrivée.

Une fonction peut être représentée de plusieurs manières. Si, par exemple, le diagramme de Venn est disponible, l'évaluation est très simple, il suffit de sélectionner l'élément de l'ensemble de démarrage ou de domaine et voir l'élément qui correspond à l'ensemble d'arrivée.

En el diagrama de la función “… es capital de… ”, representado arriba, al evaluar dicha función en el elemento “Canadá”, resulta el elemento “Ottawa”, en caso de hacerlo con “México”, resulta “Ciudad de México” et ainsi de suite.

Si la fonction est donnée sous la forme de paires bien rangées, l'évaluation est également simple: le deuxième membre du couple ordonné est l'image du premier membre. Par exemple, avec la fonction f (x) décrite par:

f (x) = (0,0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Lors de l'évaluation de la fonction de la valeur 3, le résultat est 6; Lors de l'évaluation de 5, il est 10 et ainsi de suite.

De même, une fonction peut être évaluée lorsque le graphique est disponible, à condition que la valeur que vous souhaitez évaluer y apparaisse.

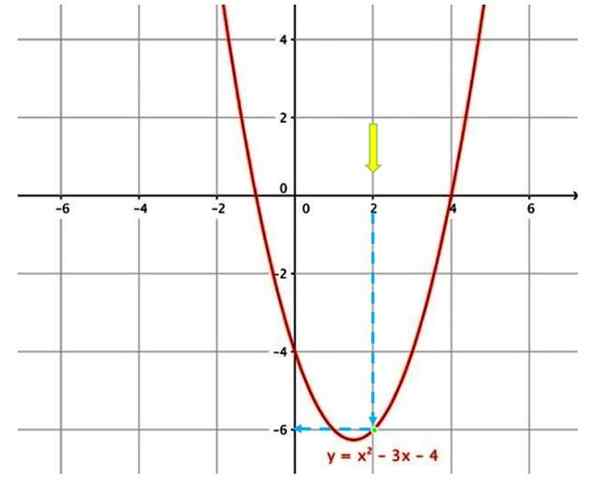Graphique pour évaluer une fonction

Par exemple, pour évaluer la fonction illustrée ci-dessus, à x = 2, la première chose est de localiser dans le graphique A x = 2 (flèche jaune).

Ensuite, vous devez vous déplacer après la flèche verticale bleue, jusqu'à ce que vous touchez la courbe (point vert). Suivez à nouveau la flèche bleue, qui indique la valeur correspondante sur l'axe vertical, par conséquent, lors de l'évaluation de la fonction à x = 2, y = −6 est obtenue.

Il peut vous servir: fonctions trigonométriques: basique, dans le plan cartésien, exemples, exercice

Évaluer une fonction donnée en notation mathématique

Dans la partie inférieure du graphique ci-dessus, la fonction graphique apparaît, mais donnée en notation mathématique, c'est-à-dire à travers une formule:

f (x) = x² - 3x - 4

Lorsque vous souhaitez évaluer la fonction dans n'importe quelle valeur x = a, vous devez trouver f (a), qui est simplement lu "f de a".

Pour trouver le résultat, x = a est remplacé dans la formule de fonction, et les opérations et calculs demandés y sont effectués.

Supposons que vous souhaitiez évaluer la fonction de l'exemple à x = −1. Cela signifie que F (−1) doit être trouvé.

La première étape consiste à remplacer x = -1 dans la fonction:

f (−1) = (−1)² - 3 ∙ (−1) - 4

Et puis, effectuez les opérations indiquées qui, dans cet exemple, sont:

• Trouvez le carré de -1: (−1)² = 1
• Soustrayez la valeur précédente du produit 3 ∙ (−1): 3 ∙ (−1) = −3
• D'après le résultat précédent, soustraire 4

f (−1) = (−1)² - 3 ∙ (−1) - 4 = 1 + 3 - 4 = 0

Le lecteur peut corroborer ce résultat, du graphique de la fonction.

La procédure décrite peut être utilisée pour évaluer la fonction à toute autre valeur de domaine. Par exemple, vous pouvez trouver F (-2), F (100) ou même F (H), où H est une valeur variable arbitraire, qui appartient au domaine de la fonction.

Évaluer une fonction à une valeur x = h 

Supposons que vous souhaitiez évaluer la fonction à une valeur arbitraire, une opération fréquente du calcul mathématique.

Dans ce cas, X est remplacé par H, de la même manière qui est fait lorsque X prend une valeur numérique, et le résultat est simplifié autant que possible.

Lorsque l'opération résultante ne peut plus être simplifiée, l'opération résultante est laissée.

Il peut vous servir: enegon: propriétés, comment faire une égon, exemples

Exemple

Vous souhaitez évaluer la fonction f (x) = x² - 3x - 4 à x = h + 1. L'approche nécessaire est la suivante:

f (h + 1) = (h + 1)² - 3 ∙ (H + 1) - 4

À droite de l'égalité, le premier terme est un produit remarquable:

(H + 1)² = H² +2h + 1

Le terme suivant est résolu par la propriété distributive:

3 ∙ (H + 1) = 3H + 3

Lorsque vous remplacez tout ce qui précède, vous avez:

f (h + 1) = (h + 1)² - 3 ∙ (H + 1) - 4 = H² +2H + 1 - (3H + 3) - 4

Les termes similaires sont réduits, par somme algébrique:

f (h + 1) = h² + 2H + 1 - 3H - 3 - 4 = H² - H - 6

Le quotient différentiel

Le quotient différentiel ou le rapport des différences d d'une fonction f (x) est défini comme:

Avec la condition h ≠ 0, ce qui est nécessaire, car la division par 0 n'est pas définie.

Ce quotient est interprété géométriquement comme la pente d'une ligne sécante à la courbe, c'est-à-dire une ligne qui passe par deux points. Les coordonnées de ces points sont: [x, f (x)] et [x + h; f (x + h)], comme le montre la figure suivante:

Le quotient différentiel équivaut à calculer la pente de la ligne sécante à la courbe, qui passe par les points indiqués. Source: Wikimedia Commons.

C'est pourquoi ce quotient apparaît dans le calcul de la dérivée d'une fonction, depuis que «H» approche la valeur 0, la ligne sécante a tendance à devenir une ligne tangente au point (x, y), car les points à intersection de La figure est si proche qu'ils tendent au même point.

Ainsi, la ligne devient tangente (intercepte la courbe en un seul point).

Il s'agit précisément de la définition de dérivée d'une fonction: la pente de la ligne tangente à la courbe en point de coordonnées (x, f (x)))).

Il peut vous servir: médias pondérés: comment il est calculé, exemples et exercices

Comme on peut le voir, le quotient différentiel nécessite d'évaluer la fonction en (x + h) et en x. Les exemples suivants illustrent comment le faire.

Exemple 1

Vous souhaitez trouver le quotient différentiel de la fonction f (x) = 2x - 3. La première étape consiste à augmenter l'évaluation de la fonction pour x = x + h, comme ceci:

f (x + h) = 2 ∙ (x + h) - 3 = 2x + 2h - 3

Ensuite, le résultat est remplacé dans la définition de D, donné précédemment:

Avec h ≠ 0.

Le numérateur est simplifié dans la mesure du possible, réduisant des termes similaires:

Enfin, les facteurs communs dans le numérateur et le dénominateur sont simplifiés:

D = 2

Exemple 2

Trouvez le quotient différentiel de la fonction f (x) = x² - 3x - 4.

Nous procédons comme dans l'exemple précédent, en trouvant le premier F (x + h), en remplaçant le résultat en D et en simplifiant le maximum:

f (x + h) = (x + h)² - 3 (x + h) - 4 = x² + 2hx + h² - 3x - 3h - 4

= 2x + H-3

Donc:

D = 2x + H-3

Où h ≠ 0.

Exercices résolus

Exercice 1

Évaluer la fonction f (x) = 2x² - 4x + 1 quand:

a) x = -1
b) x = 0
c) x = 2

Solution à

F (-1) = 2 (-1)² - 4 (-1) + 1 = 2 + 4 + 1 = 7

Solution B

f (0) = 2 (0)² - 4 (0) + 1 = 0 - 0 + 1 = 1

Solution C

f (2) = 2 ∙ 2² - 4 ∙ 2 + 1 = 8 - 8 + 1 = 1

Exercice 2

Une équipe conservationniste a déterminé que la fonction w (t) = 0.LT² + 1.8T sert à modéliser la quantité de déchets "W", en kilogrammes, qui sont jetés dans une certaine rivière, dans un temps "t", donné en jours.

Calculez la quantité de déchets jetés dans la rivière à la fin de:

a) 3 jours
b) 1 semaine
c) 1 mois

Solution à

La fonction w (t) est évaluée à t = 3 jours:

W (3) = 0.1 × 3² +1.8 × 3 = 0.9 + 5.4 = 6.3 kilogrammes

Solution B

Avant d'évaluer, vous devez passer une semaine à des jours:

1 semaine = 7 jours

W (7) = 0.1 × 7² +1.8 × 7 = 4.9 + 12.6 = 17.5 kilogrammes

Solution C

Encore une fois, il est nécessaire de transformer les mois en jours:

1 mois = 30 jours

W (30) = 0.1 × 30² +1.8 × 30 = 90 + 54 = 144 kilogrammes

Les références

1. Larson, R. 2012. Précalation. 8e. Édition. Cengage Learning.
2. Institut Monterey. Évaluation des fonctions. Récupéré de: montereyinstitute.org.
3. Stewart, J. 2007. Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
4. Sullivan, m. 1997. Précalation. 4e. Édition. Pearson Education.
5. Zill, D. 2008. Précculement avec avancées de calcul. 4e. Édition. McGraw Hill.