Formules d'énergie mécanique, concept, types, exemples, exercices

La énergie mécanique d'un objet ou d'un système est défini comme la somme de son énergie potentielle et de son énergie cinétique. Comme son nom l'indique, le système acquiert une énergie mécanique grâce à l'action de forces mécaniques telles que le poids et la force élastique.

Selon la quantité d'énergie mécanique que le corps a, il aura également la capacité d'effectuer un travail mécanique.

Figure 1. Le mouvement des voitures de montagne à rouleaux peut être décrit par la conservation de l'énergie mécanique. Source: Pixabay.

L'énergie - le type qui est - est une quantité scalaire, manquant donc de direction et de signification. Être ET_m L'énergie mécanique d'un objet, OU Son énergie potentielle et K Son énergie cinétique, la formule pour le calculer est:

ET_m = K + u

L'unité du système énergétique international de toutes sortes est le Joule, qui est abrégé comme J. 1 j équivaut à 1 n.m (Newton par mètre).

Quant à l'énergie cinétique, il est calculé comme suit:

K = ½ m.V²

Où m C'est la masse de l'objet et V Sa vitesse. L'énergie cinétique est toujours une quantité positive, car la masse et le carré de la vitesse sont. Quant à l'énergie potentielle, s'il s'agit d'une énergie potentielle gravitationnelle, vous avez:

U = m.g.H

Ici m C'est toujours la pâte, g C'est l'accélération de la gravité et H C'est la hauteur par rapport au niveau de référence ou s'il est préféré, le sol.

Maintenant, si le corps en question a une énergie potentielle élastique - il pourrait être un ressort - c'est parce qu'il est comprimé ou peut-être allongé. Dans ce cas, l'énergie potentielle associée est:

U = ½ kx²

Avec k comme la constante de ressort, ce qui indique à quel point il est facile ou difficile de le déformer et X La longueur de ladite déformation.

[TOC]

Concept et caractéristiques de l'énergie mécanique

Approfondissant la définition donnée précédemment, l'énergie mécanique dépend alors de l'énergie associée au mouvement corporel: l'énergie cinétique, plus la contribution de l'énergie potentielle, qui, comme nous l'avons dit, peut être gravitationnelle, en raison du poids et du poids et de la position qui occupe le corps avec respect du sol ou du niveau de référence.

Illustrons cela avec un exemple simple: Supposons que vous ayez un pot sur le sol et au repos. Comme il est encore, il n'a pas d'énergie cinétique, et il est également sur le terrain, un endroit où il ne peut pas tomber; Par conséquent, il manque d'énergie potentielle gravitationnelle et son énergie mécanique est 0.

Supposons maintenant que quelqu'un place le pot juste au bord d'un toit ou d'une fenêtre, à 3.0 mètres de haut. Pour cela, la personne devait faire un travail contre la gravité. Le pot a maintenant une énergie potentielle gravitationnelle, elle peut tomber de cette hauteur et son énergie mécanique n'est plus vide.

Figure 2. Un pot sur une fenêtre a une énergie potentielle gravitationnelle. Source: Pixabay.

Dans ces circonstances, le pot a ET_m = U Et cette quantité dépend de la taille et du poids du pot, comme indiqué précédemment.

Disons que le pot tombe parce qu'il était dans une position précaire. À mesure que sa vitesse augmente et avec elle son énergie cinétique, tandis que l'énergie potentielle gravitationnelle diminue, car elle perd de la hauteur. L'énergie mécanique à tout moment de la chute est:

Peut vous servir: quelles sont les amplitudes dérivées?

ET_m = U + k = ½ m.V² + m.g.H  

Forces conservatrices et non conservatrices

Lorsque le pot est à une certaine hauteur, il a une énergie potentielle gravitationnelle parce que qui l'a grimpé, a fait un travail contre la gravité. L'ampleur de ce travail vaut la même chose que celle qui fait de la gravité lorsque le pot tomber De cette même hauteur, mais il a le signe opposé, car il a été fait contre lui.

Les travaux qui forces tels que la gravité et l'élasticité ne dépend que de la position initiale et de la position finale acquise par l'objet. Peu importe la trajectoire suivie pour passer de l'une à l'autre, seules les valeurs elle-même comptent. Les forces qui se comportent de cette manière sont appelées Forces conservatrices.

Et comme ils sont conservateurs, ils permettent à leur travail d'être stocké comme une énergie potentielle dans la configuration de l'objet ou du système. C'est pourquoi le pot sur le bord de la fenêtre ou du toit, avait la possibilité de tomber, et avec elle pour développer un mouvement.

D'un autre côté, il y a des forces dont les œuvres dépendent du chemin suivi de l'objet sur lequel ils agissent. La friction appartient à ce type de forces. Les semelles de chaussures seront dépensées plus lorsque vous passerez d'un endroit à un autre sur une route avec de nombreux tours que lorsque vous optez pour un autre plus direct.

Les forces de friction font un travail qui diminue l'énergie cinétique du corps, car elle les ralentit. Et c'est pourquoi l'énergie mécanique des systèmes dans lesquels les agres de frottement ont tendance à diminuer.

Une partie du travail effectué par Force est perdue par la chaleur ou le son, par exemple.

Types d'énergie mécanique

L'énergie mécanique est, comme nous l'avons dit, la somme de l'énergie cinétique et de l'énergie potentielle. Maintenant, l'énergie potentielle peut provenir de diverses forces conservatrices: poids, force élastique et force électrostatique.

- Énergie cinétique

L'énergie cinétique est une quantité scalaire qui devient toujours le mouvement. Toute particule ou objet mobile a une énergie cinétique. Un objet qui se déplace en ligne droite a une énergie cinétique de traduction. Il en va de même s'il est en rotation, dans ce cas, il est discuté de l'énergie cinétique rotationnelle.

Par exemple, une voiture qui se déplace le long d'une route a une énergie cinétique. Également un bal de football tout en se déplaçant le long du terrain ou la personne qui marche à la hâte pour atteindre le bureau.

- Énergie potentielle

Il est toujours possible d'associer une fonction scalaire appelée énergie potentielle à une force conservatrice. Les éléments suivants se distinguent:

Énergie potentielle gravitationnelle

Celui que tous les objets ont en vertu de leur hauteur par rapport au sol, ou le niveau de référence qui a été sélectionné comme tel. À titre d'exemple, quelqu'un qui se repose sur la terrasse d'un bâtiment à 10 étages, a une énergie potentielle 0 en ce qui concerne le sol de la terrasse, mais pas en ce qui concerne la rue qui est à 10 étages en dessous.

Énergie potentielle élastique

Il est généralement stocké dans des objets tels que des ligues et des ressorts, associés à la déformation qu'ils éprouvent lors de l'étirement ou de la compression.

Énergie potentielle électrostatique

Il est stocké dans un système de charges d'électricité en équilibre, en raison de l'interaction électrostatique entre eux. Supposons qu'il y ait deux charges électriques du même signe séparé à une petite distance; Comme les frais électriques du même signe sont repoussés, il est prévu qu'un agent externe ait travaillé pour les rapprocher.

Peut vous servir: des circuits de courant alternatifs: types, applications, exemples

Une fois positionné, le système parvient à stocker le travail que l'agent a fait pour les configurer, sous forme d'énergie potentielle électrostatique.

Conservation de l'énergie mécanique

De retour dans le pot qui tombe, l'énergie potentielle gravitationnelle qu'elle avait lorsqu'elle était sur le bord du toit est transformée en mouvement cinétique de mouvement. Cela augmente au détriment du premier, mais la somme des deux reste constante, car la chute du pot est activée par la gravité, qui est une force conservatrice.

Il y a un échange entre un type d'énergie et un autre, mais la quantité d'origine est la même. Par conséquent, il est valable d'affirmer que:

Énergie mécanique initiale = énergie mécanique finale

ET_{Initial m} = E_{M final}

Alternativement:

K_initial + OU_initial = K _final + OU_final

En d'autres termes, l'énergie mécanique ne change pas et ∆E_m = 0. Le symbole "∆" signifie variation ou différence entre un montant final et une initiale.

Pour appliquer correctement le principe de conservation de l'énergie mécanique à la résolution de problèmes, il est nécessaire de:

-Elle ne s'applique que lorsque les forces agissant sur le système sont conservatrices (gravité, élastique et électrostatique). Dans ce cas: ∆E_m = 0.

-Le système d'étude doit être isolé. Il n'y a aucun transfert d'énergie en aucune façon.

-Si dans un problème, la fracture apparaît, alors ∆E_m ≠ 0. Même ainsi, le problème pourrait être résolu en trouvant le travail effectué par les forces conservatrices, car c'est la cause de la diminution de l'énergie mécanique.

Déduction de la conservation de l'énergie mécanique

Supposons qu'une force conservatrice agit sur le système qui fait un travail W. Ce travail provoque un changement d'énergie cinétique:

W = ∆K (Théorème de l'énergie du travail cinétique)

Il est important de noter que le théorème de travail cinétique est applicable même dans le cas de forces non conservatrices.

D'un autre côté, le travail est également responsable du changement d'énergie potentielle, et dans le cas d'une force conservatrice, le changement d'énergie potentielle est défini comme le négatif de ce travail:

W = -∆u

Correspondant à ces équations, car les deux se réfèrent au travail effectué sur l'objet:

∆K = -∆U 

K_F - K_soit = - (u_F - OU_soit)

Les indices symbolisent "final" et "initiale". Regroupement:

K_F + OU_F = K_soit + OU_soit                                                    

Exemples d'énergie mécanique

De nombreux objets ont des mouvements complexes, dans lesquels il est compliqué de trouver des expressions pour la position, la vitesse et l'accélération en fonction du temps. Dans de tels cas, l'application du principe de conservation de l'énergie mécanique est une procédure plus efficace que d'essayer d'appliquer directement les lois de Newton.

Regardons quelques exemples dans lesquels l'énergie mécanique est préservée:

-Un skieur qui glisse en descente sur des collines enneigées, à condition que l'absence de frottement soit supposée. Dans ce cas, le poids est la force causative du mouvement tout au long de la trajectoire.

-Chariots de montagne russes, C'est l'un des exemples les plus typiques. Ici aussi le poids est la force qui définit le mouvement et l'énergie mécanique est conservée s'il n'y a pas de frottement.

Peut vous servir: énergie d'ionisation

-Le pendule simple Il se compose d'une masse sujette à une corde inextensible - elle ne change pas la longueur qui se sépare brièvement de la verticale et est autorisée à osciller. Nous savons qu'il finira par s'arrêter en raison de la friction, mais lorsque la friction n'est pas considérée, l'énergie mécanique est également préservée.

-Un bloc qui a un impact sur un printemps Fixé par une extrémité au mur, tous mis sur une table très lisse. Le bloc comprime le ressort, parcourt une certaine distance et est ensuite tiré dans la direction opposée, car le ressort s'étire. Ici, le bloc acquiert son énergie potentielle grâce au travail qui fait le ressort dessus.

-Printemps et balle: Lorsqu'un ressort est comprimé par une balle, ce rebond. C'est parce que lorsque le ressort est libéré, l'énergie potentielle devient une énergie cinétique dans la balle.

-Saut de trampoline: Cela fonctionne comme un printemps, faisant la promotion élastique de la personne qui saute dessus. Cela utilise son poids lors du saut, avec lequel il déforme le trampoline, mais celui-ci, lors de son retour à sa position d'origine, donne l'impulsion au pull.

figure 3. Le tremplin agit comme un printemps, faisant la promotion des gens qui sautent dessus. Source: Pixabay.

Exercices résolus

- Exercice 1

Un objet de masse M = 1 kg est tombé par une rampe d'une hauteur de 1 m. Si la rampe est extrêmement lisse, calculez la vitesse du corps juste au moment où le ressort entre en collision.

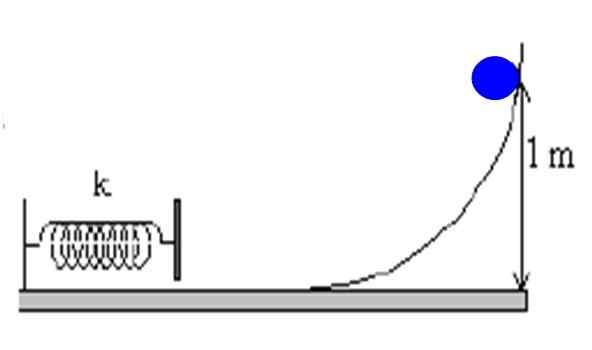Figure 4. Un objet descend sur une rampe sans frottement et comprime un ressort qui est attaché au mur. Source: F. Zapata.

Solution

La déclaration rapporte que la rampe est fluide, ce qui signifie que la seule force qui agit sur le corps est son poids, une force conservatrice. Ainsi, il est indiqué pour appliquer la conservation de l'énergie mécanique entre tous les points de la trajectoire.

Considérez les points marqués dans la figure 5: A, B et C.

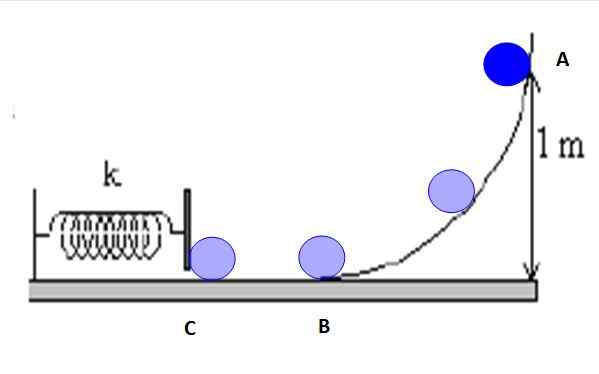Figure 5. Le chemin qui suit l'objet est la friction et l'énergie mécanique est conservée entre n'importe quelle paire de points. Source: F. Zapata.

Il est possible d'établir la conservation de l'énergie entre A et B, B et C ou A et C, ou l'un des points intermédiaires de la rampe. Par exemple, entre A et C, vous avez:

Énergie mécanique à a = énergie mécanique en c

ET_mame = E_MC

K_POUR + OU_POUR = K_C + OU_C

½ m.V_POUR² + m.g.H_POUR = ½ m V_C² + m.g.H_C

Comme il est libéré du point A, la vitesse V_POUR = 0, d'autre part h_C = 0. De plus, la masse est annulée, car c'est un facteur commun. Ensuite:

g.H_POUR = ½ V_C²

V_C²= 2 g.H_POUR

- Exercice 2

Trouvez la compression maximale que le ressort de l'exercice résolue 1 expérimentera si la constante élastique de même est de 200 n / m.

Solution

La constante élastique du ressort indique la force à appliquer pour déformer une unité de longueur. Étant donné que la constante de ce printemps vaut k = 200 n / m, cela indique que 200 N sont nécessaires pour le comprimer ou l'étirer 1 m.

Être X La distance que l'objet comprime le ressort avant de s'arrêter au point D:

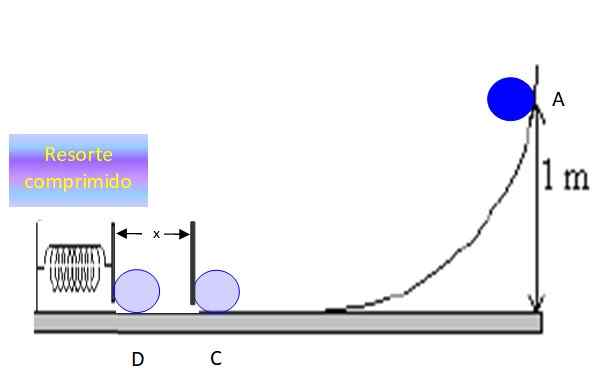Figure 6. L'objet comprime le ressort d'une distance x et s'arrête momentanément. Source: F. Zapata.

La conservation de l'énergie entre les points C et D établit que:

K_C + OU_C = K_D + OU_D

Au point C, il n'a pas d'énergie potentielle gravitationnelle, car sa hauteur est de 0, mais elle a une énergie cinétique. En d il s'est complètement arrêté, donc là k_D = 0, mais à la place, vous avez à la disposition l'énergie potentielle du ressort comprimé u_D.

La conservation de l'énergie mécanique reste:

K_C = U_D

½ mV_C² = ½ kx²

 

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
2. Figueroa, D. 2005. Série: Physique pour la science et l'ingénierie. Volume 1. Cinématique. Édité par Douglas Figueroa (USB).
3. Chevalier, r.  2017. Physique pour les scientifiques et l'ingénierie: une approche stratégique. Pearson.
4. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. Volume 1.
5. Wikipédia. Énergie mécanique.Récupéré de: est.Wikipédia.org.