Helmholtz Free Energy Units, comment il est calculé, exercices résolus

La Helmholtz Free Energy Il s'agit d'un potentiel thermodynamique qui mesure le travail utile d'un système fermé dans des conditions de température et de volume constantes. L'énergie libre de Helmholtz est indiquée comme F Et il est défini comme la différence par rapport à l'énergie interne OU moins le produit de température T Pour l'entropie S:

F = u - t⋅s

Puisqu'il s'agit de l'énergie, il est mesuré en joules dans le système international (SI), bien que d'autres unités appropriées puissent également être des ergios (CG), des calories ou des volts électroniques (EV).

Figure 1. Définition de l'énergie de Helmholtz. Source: Pixabay.

La variation négative de l'énergie de Helmholtz pendant un processus est assimilée au travail maximum que le système peut effectuer dans un processus isocorique, c'est-à-dire à un volume constant. Lorsque le volume n'est pas constant, une partie de ce travail peut être effectuée sur l'environnement.

Dans ce cas, nous nous référons au travail dans lequel le volume ne varie pas, comme les travaux électriques: dw = φdq, avec φ comme potentiel électrique et q comme charge électrique.

Si la température est également constante, l'énergie de Helmholtz est minimisée lorsque l'équilibre est atteint. Pour tout cela, l'énergie de Helmholtz est particulièrement utile dans les processus de volume constant. Dans ce cas, vous avez:

- Pour un processus spontané: Δf < 0

- Lorsque le système est en équilibre: Δf = 0

- Dans un processus non spontané: Δf> 0.

[TOC]

Comment Helmholtz Free Energy est-il calculé?

Comme indiqué au début, l'énergie de Helmholtz est définie comme "l'énergie ou le système interne, à l'exception du produit de la température absolue du système, par l'entropie du système":

F = u - t⋅s

Il est fonction de la température T et du volume V. Les étapes pour visualiser ceci sont les suivantes:

Peut vous servir: électrons internes

- À partir de la première loi de la thermodynamique, de l'énergie interne ou est liée à l'entropie S du système et de son volume V pour les processus réversibles à travers la relation différentielle suivante:

du = dq - dw = tds - pdv

Cela suit que l'énergie interne ou est fonction des variables S et V, donc:

U = u (s, v)

- Maintenant la définition de F Et il est dérivé:

df = du - d (ts) = du - tds - sdt

- Remplacement là-bas l'expression différentielle obtenue pour DU dans la première étape, reste:

Df = TDS - PDV - TDS - SDT = -SDT - PDV

- Enfin, il est conclu que F est fonction de la température T et du volume V et peut être exprimé comme:

F = f (t, v)

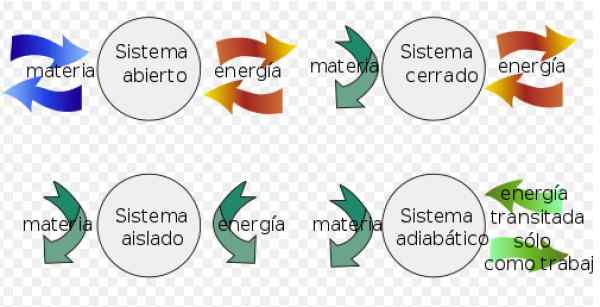Figure 2. Hermann von Helmholtz (1821-1894), physicien et médecin allemand, reconnu pour ses contributions à l'électromagnétisme et à la thermodynamique, entre autres domaines scientifiques. Source: Wikimedia Commons.

Processus spontanés

L'énergie de Helmholtz peut être appliquée comme un critère général de spontanéité dans les systèmes isolés, mais avant que certains concepts ne soient spécifiés:

- UN Système fermé Il peut échanger de l'énergie avec l'environnement, mais ne peut pas échanger de l'importance.

- Au lieu d'un système isolé n'échange pas de matière ou d'énergie avec l'environnement.

- Enfin un système ouvert Échange de matière et d'énergie avec l'environnement. 

figure 3. Systèmes thermodynamiques. Source: Wikimedia Commons. Fjgar (bis) [cc by-sa (https: // CreativeCommons.Org / licences / by-sa / 4.0)].

Dans les processus réversibles, la variation de l'énergie interne est calculée comme suit:

Du = TDS - PDV

Supposons maintenant un processus de volume constant (isocomique), dans lequel le deuxième terme de l'expression précédente a une contribution nulle. Il faut également se rappeler que selon le INÉGALITÉ DE CLAUSIUS: 

ds ≥ dq / t

Une telle inégalité s'applique à un système thermodynamique isolé.

De sorte que pour un processus (réversible ou non) dans lequel le volume est maintenu constant est rempli:

Peut vous servir: acide phosphorique (H3PO4)

T ds ≥ du (Au volume fixe)

En tenant compte de cela:

df = du - t ds 

Nous devrons dans un processus isocorique à température constante est rempli: Df ≤ 0, Comme indiqué au début.

De sorte que l'énergie de Helmholtz F est une quantité décroissante dans un processus spontané alors qu'il s'agit d'un système isolé. F atteint sa valeur minimale et stable lorsque l'équilibre réversible a été atteint.

Exercices résolus

Exercice 1

Calculez la variation de l'énergie libre de Helmholtz F pour 2 moles de gaz idéal à une température de 300k pendant une expansion isotherme qui conduit au système d'un volume initial de 20 litres à un volume final de 40 litres.

Solution

À partir de la définition de f:

F = u - t s

Ensuite, une variation finie de f, appelée ΔF, sera:

Δf = ΔU - T ΔS

Comme l'instruction indique que la température est constante: Δt = 0. Cependant, dans les gaz idéaux, l'énergie interne ne dépend que de sa température absolue, mais comme il s'agit d'un processus isotherme, alors ΔU = 0 et Δf = - t ΔS. Pour les gaz idéaux, la variation d'entropie d'un processus isotherme est écrite comme ceci: 

ΔS = n.R.LN (V₂/ V₁)

Appliquer cette expression:

ΔS = 2 moles x 8,314 J / (k mol) x ln (40L / 20L) = 11,53 J / K

Enfin, le changement de l'énergie de Helmholtz est:

Δf = - t ΔS = - 300K x 11,53 J / K = -3457,70 J.

Exercice 2

À l'intérieur d'un cylindre, il y a un piston qui le divise en deux sections et de chaque côté du piston il y a n moles d'un gaz monoatomique idéal, comme le montre la figure ci-dessous.

Les parois des cylindres sont de bons conducteurs de chaleur (diathermique) et sont en contact avec un réservoir de température t_soit.

Le volume initial de chacune des sections de cylindre est V_1i et V_2i, tandis que ses volumes finaux sont V_1F et V_2F Après un déplacement quasi. Le piston se déplace au moyen d'un piston qui traverse hermétiquement les tapas à deux cylindres.

Il peut vous servir: Tecnecio (TC): structure, propriétés, utilisations, obtention

On demande de trouver:

a) Le changement de l'énergie interne du gaz et le travail effectué par le système et

b) Variation énergétique de Helmholtz.

Solution à

Au fur et à mesure que le piston se déplace quasi-ouest, la force externe appliquée au piston doit équilibrer la force due à la différence de pression dans les deux sections du cylindre.

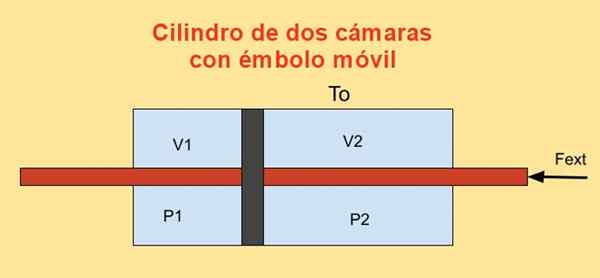Figure 4. Variation de l'énergie libre F dans un cylindre avec deux caméras. Source: F. Zapata.

Le travail Dwing Fabriqué par force externe F_ext pendant un déplacement infinitésimal Dx est:

Dw = - f_ext Dx = (p₁ - P₂) A dx = p₁ Dv₁ + P₂ Dv₂

Où la relation a été utilisée Dv₁ = - DV₂ = Un dx, être pour La zone de piston. D'un autre côté, la variation de l'énergie de Helmholtz est: 

Df = -sdt - pdv

Étant donné que pendant le processus, la température ne change pas, alors dt = 0 et Df = - pdv. En appliquant cette expression à chaque section du cylindre que vous avez:

dw = p₁ Dv₁ + P₂ Dv₂ = - df₁ - Df₂

Être F₁  et F₂ Les énergies de Helmholtz dans chacune des caméras.

Le travail final en w peut être calculé à partir de la variation finie de l'énergie de Helmholtz de chaque caméra:

W = -Δf₁ - ΔF₂

Solution B

Pour trouver le changement d'énergie de Helmholtz, la définition est utilisée: F = u - t s. Comme dans chaque caméra, vous avez un gaz monoatomique idéal à température constante T_soit, L'énergie interne ne change pas (ΔU = 0), de sorte que: Δf = - t_soit ΔS. En outre:

ΔS = nr ln (v_F/Scie)

Qu'en le remplaçant permet enfin le travail effectué est: 

W = -t_soit Nr ln (V_1F / V_1i) -To nr ln (v_2F / V_2i) = -Δf₁ -ΔF₂

W = - à nr ln [(v_1F ⋅ V_1i) / (V_{2F .}V_2i)] = - Δf_total

Être ΔF_total La variation totale de l'énergie de Helmholtz.

Les références

1. Castaños e. Exercices d'énergie libre. Récupéré de: lidiaconlachimica.Wordpress.com
2. Bibliothèque. Helmholtz Energy. Récupéré de: Chem.Bibliothèque.org
3. Bibliothèque. Qu'est-ce que l'énergie libre. Récupéré de: Chem.Bibliothèque.org
4. Wikipédia. Helmholtz Energy. Récupéré de: est.Wikipédia.com
5. Wikipédia. Helmholtz Free Energy. Récupéré de: dans.Wikipédia.com