Unités d'énergie libre de Gibbs, comment il est calculé, exercices résolus

La Gibbs Free Energy (communément appelé g) est un potentiel thermodynamique défini comme la différence d'enthalpie H, à l'exception du produit de la température T, par l'entropie S du système:

G = h - t s

Gibbs Free Energy est mesuré en Joules (selon le système international), en Ergios (pour le système de ligue des unités), en calories ou en électrons (Pour Electro Volts).

Figure 1. Diagramme montrant la définition de l'énergie de Gibbs et sa relation avec les autres potentiels thermodynamiques. Source: puissance nucléaire.filet.

Dans les processus qui se produisent à une pression et à une température constantes, la variation de l'énergie libre de Gibbs est Δg = ΔH - T ΔS. Dans de tels processus, (g) représente l'énergie disponible dans le système qui peut devenir un travail.

Par exemple, dans les réactions chimiques exothermiques, l'enthalpie diminue tandis que l'entropie augmente. Dans la fonction Gibbs, ces deux facteurs sont contrecarrés, mais uniquement lorsque l'énergie de Gibbs diminue la réaction se produit spontanément.

Donc, si la variation de G est négative, le processus est spontané. Lorsque la fonction Gibbs atteint son minimum, le système atteint un équilibre stable. En bref, dans un processus pour lequel la pression et la température restent constantes, nous pouvons affirmer:

- Si le processus est spontané, alors ΔG < 0

- Lorsque le système est en équilibre: Δg = 0

- Dans un processus non spontané, il augmente: Δg> 0.

[TOC]

Comment est-il calculé?

Gibbs Free Energy (G) est calculé par la définition donnée au début:

G = h - tn

À son tour, l'enthalpie H est un potentiel thermodynamique défini comme:

H = u + p v

- Pas à pas

Ensuite, une analyse étape par étape sera effectuée pour connaître les variables indépendantes dont l'énergie Gibbs est une fonction:

1- de la première loi de la thermodynamique, l'énergie interne est liée à l'entropie S du système et à son volume V pour les processus réversibles à travers la relation différentielle:

Il peut vous servir: bromure d'éthidium: structure, propriétés, utilisations, toxicité

du = dq - dw = tds - pdv

De cette équation, il s'ensuit que l'énergie interne U est fonction des variables S et V:

U = u (s, v)

2- À partir de la définition de H et de la prise du différentiel est obtenu:

dh = du + d (p v) = du + vdp + pdv

3- Sécéder à l'expression de DU obtenu dans (1) vous devez:

Dh = TDS - PDV + VDP + PDV = TDS + VDP

De là, il est conclu que l'enthalpie H dépend de l'entropie S et de la pression P, c'est-à-dire:

H = h (s, p)

4- Maintenant, le différentiel total de Gibbs libre est calculé pour obtenir:

Dg = dh -tds -sdt = tds + vdp -tds -sdt

Où dh a été remplacé par l'expression trouvée dans (3).

5- Enfin, en simplifiant vous obtenez: Dg = VDP - SDT, Il est clair que l'énergie libre G dépend de la pression et de la température t comme:

G = g (p, t)

- Relations thermodynamiques de Maxwell

D'après l'analyse dans la section précédente, il s'ensuit que l'énergie interne d'un système est fonction de l'entropie et du volume:

U = u (s, v)

Puis le différentiel de OU être:

du = ∂_SU |_V Ds + ∂_VU |_S Dv = TDS - PDV

De cette expression dans des dérivés partiels, les relations thermodynamiques de Maxwell So-appelées peuvent être déduites. Les dérivés partiels s'appliquent lorsqu'une fonction dépend de plusieurs variables et est facilement calculée en appliquant le théorème de la section suivante.

La première relation de Maxwell

 ∂_VT |_S = -Mon_SP |_V 

Pour accéder à cette relation, le Théorème de Claiaut - Schwarz sur les dérivés partiels, qui indique ce qui suit:

"Les dérivés mixtes du second ordre avec les variables échangés sont les mêmes, à condition que les fonctions à dériver sont continues et différenciables".

La deuxième relation de Maxwell

À partir de ce qui a été démontré au point 3 de la section précédente:

Peut vous servir: facteurs qui affectent la solubilité

H = h (s, p) et dh = tds + vdp

Peut être obtenu:

 ∂_PT |_S = ∂_SV |_P 

Procéder de manière similaire avec Gibbs Free Energy G = g (p, t) Et avec l'énergie libre de Helmholtz F = f (t, v) Pour obtenir les deux autres relations thermodynamiques de Maxwell. 

Figure 2. Josiah Gibbs (1839-1903) était un physicien américain, chimiste et mathématicien qui a fait de grandes contributions à la thermodynamique. Source: Wikimedia Commons.

Les quatre relations thermodynamiques de Maxwell 

1- associé à l'énergie interne u: ∂_VT |_S = -Mon_SP |_V

2- Celui obtenu à partir de l'enthalpie h: ∂_PT |_S = ∂_SV |_P 

3- lié à l'énergie de Helmholtz F: ∂_TP |_V = ∂_VS |_T 

4- lié à l'énergie libre de Gibbs G: ∂_TV |_P = -Mon_PS |_T

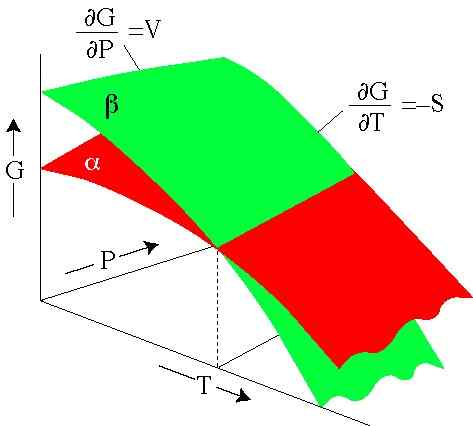Figure 2. L'énergie de Gibbs dépend de la pression et de la température. Chaque surface représente une phase. (Serc.Carleton.Edu)

Exercices résolus

Exercice 1

Calculez la variation de l'énergie libre de Gibbs pour 2 moles de gaz idéal à une température de 300k lors d'une expansion isotherme qui conduit au système de volume initial de 20 litres à un volume final de 40 litres.

Solution

Se souvenir de la définition de l'énergie libre de Gibbs est:

G = h - t s

Alors une variation finie de f sera:

ΔG = ΔH - T ΔS, Depuis Δt = 0

Dans l'enthalpie des gaz idéaux ne dépend que de sa température absolue, mais comme il s'agit d'un processus isotherme, alors ΔH = 0 et ΔG = - T ΔS.

Pour les gaz idéaux, la variation d'entropie d'un processus isotherme est: 

ΔS = nr ln (v₂/ V₁)

Qui s'appliquait au cas de cet exercice que nous avons:

ΔS = 2 moles x 8,314 J / (k mol) x ln (40L / 20L) = 11,53 J / K

Ensuite, nous pouvons obtenir le changement de l'énergie de Helmholtz:

Δg = - 300k x 11,53 J / K = -3457,70 J.

Exercice 2

Compte tenu du fait que l'énergie libre de Gibbs est fonction de la température et de la pression g = g (t, p); Déterminez la variation de g pendant un processus dans lequel la température ne change pas (isotherme) pour n moles d'un gaz monoatomique idéal.

Peut vous servir: hydroxyde de strontium (SR (OH) ₂)

Solution

Comme démontré ci-dessus, le changement de l'énergie de Gibbs ne dépend que du changement de température T et du volume V, de sorte qu'une variation infinitésimale de celui-ci est calculée selon:

Dg = -sdt + vdp

Mais s'il s'agit d'un processus dans lequel la température est constante, DF = + VDP, donc une variation finie de la pression ΔP conduit à un changement de l'énergie Gibbs donnée par:

ΔG = + ∫ VDP = + ∫ (n r t) dp / p = + n r t ln (Δp)

Utilisation de l'équation de gaz idéale:

P v = n r t

Au cours d'un processus isotherme, il se produit que:

D (p v) = p dv + v dp = 0

C'est-à-dire:

dp / p = - dv / v

Ainsi, le résultat précédent peut être écrit en fonction de la variation de volume ΔV:

ΔG = + ∫ VDP = + ∫ (n r t) dp / p = - ∫ (n r t) dv / v = -n r t ln (Δv)

Exercice 3

Compte tenu de la réaction chimique suivante:

N₂0 (g) + (3/2) ou₂ (g) ↔️₂ (g) à température t = 298 K

Trouvez la variation de l'énergie libre de Gibbs et par le résultat obtenu, indiquez s'il s'agit ou non d'un processus spontané.

Solution

Sous les étapes:

- Première étape: réaction enthalpies

ΔHr = 2 * ΔH (non₂ (g))) - ΔH (n₂0 (g)) = 2 * 33.2-81.6 = -15.2kj / mol

- Deuxième étape: la variation de l'entropie de réaction

ΔSr = 2 * s (non₂ (g)) - s (n₂0 (g)) - (3/2) s (ou₂ (g)) = 2 * 240,1 - 220,1 - 1,5 * 205.2 = -47,7 J / (mol * k).

- Troisième étape: variation de la fonction gibbs

Cette valeur déterminera l'équilibre entre la diminution de l'énergie et l'augmentation de l'entropie pour savoir si la réaction est enfin spontanée ou non.

Δgr = ΔHr -T ΔSr = -15.2 -298 * (-47,7) = -985,4 J / mol

Comme il s'agit d'une variation négative de l'énergie de Gibbs, on peut conclure qu'il s'agit d'une réaction spontanée à la température de 298 K = 25 ºC.

Les références

1. Castaños e. Exercices d'énergie libre. Récupéré de: lidiaconlachimica.Wordpress.com.
2. Cengel, et. 2012. Thermodynamique. 7e édition. McGraw Hill.
3. Bibliothèque. Gibbs Free Energy. Récupéré de: Chem.Bibliothèque.org
4. Bibliothèque. Qu'est-ce que l'énergie libre. Récupéré de: Chem.Bibliothèque.org
5. Wikipédia. Gibbs Free Energy. Récupéré de: est.Wikipédia.com
6. Wikipédia. Gibbs Free Energy. Récupéré de: dans.Wikipédia.com