Propriétés de l'égon, comment faire un enegon, exemples

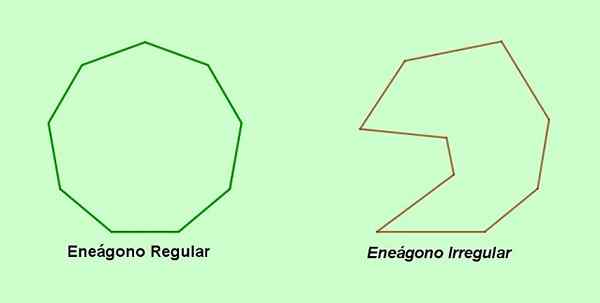
UN Évente C'est un polygone de neuf côtés et neuf sommets, qui peuvent être réguliers ou non. La dénomination de l'égon vient du grec et se compose des mots grecs Ennéa (Neuf et Gonon (angle).

Un nom alternatif pour le polygone à neuf faces est un mot non mot qui vient du latin non-u (Neuf et Gonon (sommet). D'un autre côté, si les côtés ou les angles de l'enegon sont inégaux les uns aux autres, il y a alors un Enegon irrégulier. Si au contraire, les neuf côtés et les neuf angles de l'enegon sont égaux, alors c'est un Enegon régulier.

Figure 1. Enegon régulier et égon irrégulier. (Élaboration propre)

[TOC]

Propriétés de l'égon

Pour un polygone de n côtés, la somme de ses angles internes est:

(N - 2) * 180º

Dans l'Enegon, ce serait n = 9, donc la somme de ses angles internes est:

SA = (9 - 2) * 180º = 7 * 180º = 1260º

Dans n'importe quel polygone, le nombre de diagonales est:

D = n (n - 3) / 2 et dans le cas d'Enegon, comme n = 9, vous devez d = 27.

Enegon régulier

Dans l'enegon ou le non -agon ordinaire.

Il est alors nécessaire de mesurer les angles internes d'une évente est de 1260º / 9 = 140º.

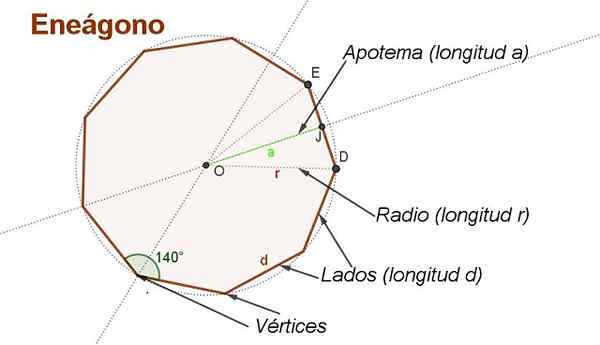Figure 2. Apothème, radio, côtés, angles et sommets d'une égon ordinaire. (Élaboration propre)

Pour déduire la formule de la zone d'une égon ordinaire sur le côté d Il est pratique de faire des constructions auxiliaires, comme celles illustrées à la figure 2.

Le centre est SOIT Dessin les méditrices de deux côtés adjacents. Centre SOIT Equidiste des sommets.

Un rayon de longueur r C'est le segment qui va du centre SOIT À un sommet de l'enegon. Les radios sont illustrées à la figure 2 Dyerne et Oe de longueur r.

Peut vous servir: symétrie

L'apothème est le segment qui va du centre au milieu d'un côté de l'Enegon. Par exemple OJ C'est un apothème dont la longueur est pour.

Zone d'un côté connu en égon et apothème

Nous considérons le triangle ODE De la figure 2. La zone de ce triangle est le produit de sa base DE en hauteur OJ divisé par 2:

Zone ODE = (De * oj) / 2 = (D * a) / 2

Comme il y a 9 triangles de la même zone dans l'Enegon, il est alors conclu que la zone de même est:

Zone d'égon = (9/2) (d * a)

Zone d'une égon connu

Si seule la longueur de l'enegon est connue, il est alors nécessaire de trouver la longueur d'apothème pour pouvoir appliquer la formule de la section précédente.

Nous considérons le triangle Oje Rectangle dans J (Voir figure 2). Si le rapport trigonométrique de couple est appliqué, il est obtenu:

donc(∡OEJ) = OJ / / Par exemple.

L'angle ∡oej = 140º / 2 = 70º, pour être Eo Bissectrice de l'angle interne de l'enegon.

D'autre part, OJ C'est l'apothème de longueur pour.

Alors comme J C'est un point médian de Élégant Il suit que Ex = d / 2.

Le remplacement des valeurs ci-dessus dans la relation de la tangente est:

Tan (70º) = A / (d / 2).

Maintenant, nous effacons la longueur de l'apothème:

A = (d / 2) Bronzage (70º).

Le résultat précédent est remplacé dans la formule de la zone pour obtenir:

Zone d'égon = (9/2) (d * a) = (9/2)( D * (d / 2) Tan (70º))

Enfin, il y a la formule qui permet d'obtenir la zone Enegon ordinaire si seule la longueur est connue d de ses côtés:

Zone d'égon = (9/4) D² Tan (70º) = 6 1818 D²

Le périmètre de l'enegon ordinaire connaît son côté

Le périmètre d'un polygone est la somme de ses côtés. Dans le cas de l'enegon, comme chacun des côtés, il mesure une longueur d, Son périmètre sera la somme de neuf fois d, c'est-à-dire:

Peut vous servir: équations polynomiales

Périmètre = 9 jours

Le périmètre de l'Enegon a connu sa radio

Considérant le triangle Oje Rectangle dans J (Voir figure 2), la raison trigonométrique Cosen est appliquée:

cos (∡OEJ) = Par exemple / / Oe = (d / 2) / r

Où êtes-vous obtenu:

D = 2r cos (70º)

En substituant ce résultat, la formule de périmètre est obtenue en fonction du rayon de l'égon:

Périmètre = 9 jours = 18 r cos (70º) = 6 1564 R

Comment faire une égon régulière

1- Pour construire une égon ordinaire, avec une règle et une boussole, elle est basée sur la circonférence c qui circonscrit à l'enegon. (Voir figure 3)

2- deux lignes perpendiculaires sont tracées à travers le centre ou la circonférence. Ensuite, les intersections A et B de l'une des lignes sont marquées de la circonférence.

3- avec la boussole, faisant du centre dans l'interception b et ouvrant égal au rayon bo.

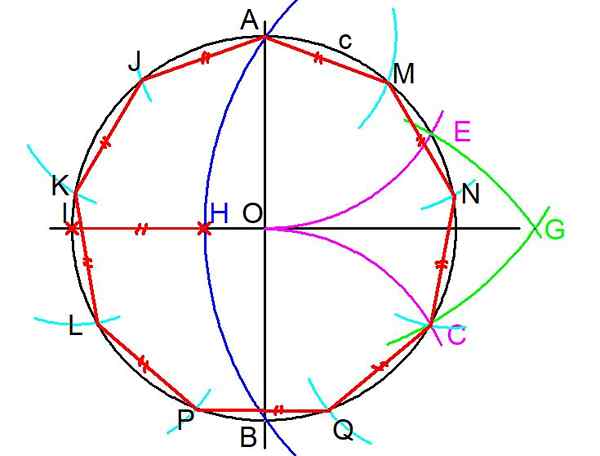figure 3. Étapes pour construire une égon ordinaire. (Élaboration propre)

4- L'étape précédente est répétée mais faisant un centre dans A et Radio Ao une arche est dessinée qui intercepte la circonférence C au point E.

5- avec une ouverture et un centre AC dans un arc de circonférence est dessiné. De même avec l'ouverture de BE et du centre B, une autre arche est dessinée. L'intersection de ces deux arches est marquée comme un G.

6- Le centre de fabrication en g et avec une ouverture de Ga, un arc est dessiné qui intercepte l'axe secondaire (horizontal dans ce cas) au point H. L'intersection de l'axe secondaire est marquée de la circonférence d'origine C comme je.

7- La longueur du segment IH est égale à la longueur D sur le côté de l'enegon.

8- avec une ouverture de boussole IH = D Les arches centrales sont successivement dessinées sur Radio AJ, Centro J Radio AK, KL Radio KL et Centro L Radio LP.

Il peut vous servir: transformations linéaires: propriétés, quels sont les types, les types, les exemples

9- De même, à partir de A et sur le côté droit, les arcos radio IH = D sont dessinés sur les points C d'origine C de circonférence M, N, C et Q.

10- Enfin, les segments AJ, JK, KL, LP, AM, MN, NC, CQ et enfin PB sont dessinés.

Il convient de noter que la méthode de construction n'est pas entièrement exacte, car il peut être vérifié que le dernier côté PB est de 0,7% plus long que les autres côtés. À ce jour, une méthode de construction et de construction de boussole n'est pas connue qui est 100% précise.

Exemples

Certains exemples résolus seront abordés ci-dessous.

Exemple 1

Vous voulez construire une égon ordinaire dont les côtés mesurent 2 cm. Quelle radio devrait-elle la circonférence qui doit circonscrire, de sorte que lors de l'application de la construction décrite précédemment, le résultat souhaité est obtenu?

Solution:

Dans une section antérieure, la formule qui relie le rayon r de la circonférence circonscrite avec le dégon régulier D a été déduite:

D = 2r cos (70º)

Effacer R de l'expression précédente que nous avons:

R = d / (2 cos (70º))) = 1 4619 * D

Le remplacement de la valeur d = 2 cm dans la formule précédente, un rayon de 2,92 cm est obtenu.

Exemple 2

Quelle est la superficie d'une élégon côté 2 cm régulier de 2 cm?

Solution:

Pour répondre à cette question, vous devez vous référer à la formule, précédemment démontrée, qui vous permet de trouver la zone d'une égon connue de la longueur D sur le côté:

Zone d'égon = (9/4) D² Tan (70º) = 6 1818 D²

Le remplacement de D pour sa valeur de 2 cm dans la formule antérieure est obtenu:

Zone d'égon = 24,72 cm

Les références

1. C. ET. POUR. (2003). Éléments de géométrie: avec des exercices et une géométrie de la boussole. Université de Medellin.
2. Campos, F., Cerecedo, f. J. (2014). Mathématiques 2. Groupe éditorial de Patria.
3. Libéré, k. (2007). Découvrir les polygones. Benchmark Education Company.
4. Hendrik, V. (2013). Polygones généralisés. Birkhäuser.
5. Iger. (s.F.). Mathématiques Premier semestre Tacaná. Iger.
6. JR. Géométrie. (2014). Polygones. Lulu Press, Inc.
7. Miller, Heeren et Hornsby. (2006). Mathématiques: raisonnement et applications (dixième édition). Pearson Education.
8. Patiño, m. (2006). Mathématiques 5. Progreso éditorial.