Caractéristiques et exemples des ellipsoïdes

Il ellipsoïde C'est une surface dans l'espace qui appartient au groupe de surfaces quadriques et dont l'équation générale est de la forme:

Hache² + Par² + CZ² + Dxy + exz + fyz + gx + hy + iz + j = 0

C'est l'équivalent à trois dimensions d'une ellipse, caractérisée par des traces elliptiques et circulaires dans certains cas particuliers. Les traces sont les courbes qui sont obtenues lors de la croisement de l'ellipsoïde avec un plan.

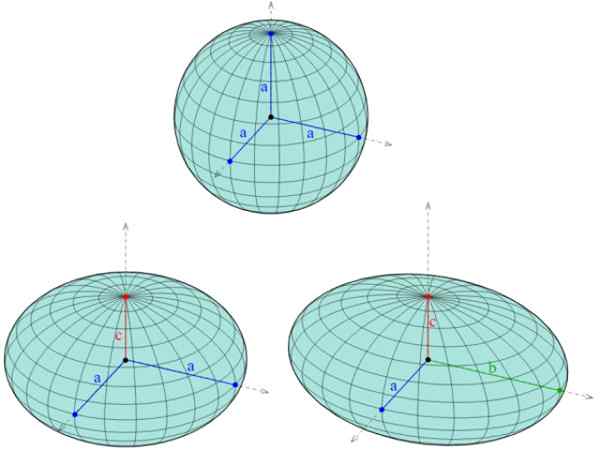
Figure 1. Trois ellipsoïdes différents: au-dessus d'une sphère dans laquelle les trois demi-semi sont les mêmes, jusqu'à la gauche un sphéroïde, avec deux demi-axes à moitié et à-un et enfin à droite, un sphéroïde triaxial, avec trois axes de longueur différente. Source: Wikimedia Commons. AG2GAEH / CC BY-S (https: // CreativeCommons.Org / licences / by-sa / 4.0)

En plus de l'ellipsoïde, il existe cinq autres quadriques: hyperboloïde d'une feuille et deux feuilles, deux types de paraboloïde (hyperbolique et elliptique) et le cône elliptique. Ses traces sont également coniques.

L'ellipsoïde peut également être exprimé par l'équation standard dans les coordonnées cartésiennes. Un ellipsoïde axé sur l'origine (0,0,0) et exprimé de cette manière, rappelle l'ellipse, mais avec un terme supplémentaire:

Les valeurs de pour, b et c Ce sont des nombres réels supérieurs à 0 et représentent la moitié ellipsoïde.

[TOC]

Caractéristiques des ellipsoïdes

- Équation standard 

L'équation standard des coordonnées cartésiennes de l'ellipse s'est concentrée sur le point (H, K, M) est:

- Équations paramétriques ellipsoïdes

Dans les coordonnées sphériques, l'ellipsoïde peut être décrit comme suit:

x = a sin θ. cos φ

y = b sin θ. péché φ

Z = c cos θ

Le semi-out ellipsoïde est toujours a, b et c, tandis que les paramètres sont les angles θ et φ de la figure suivante:

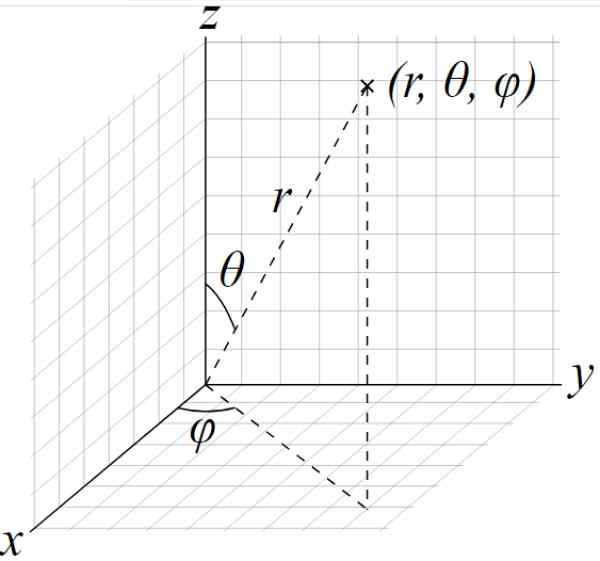Figure 2. Le système de coordonnées sphériques. L'ellipsoïde peut être paramétré à l'aide des angles illustrés thêta et phi comme paramètres. Source: Wikimedia Commons. Domaine des angegs / pub.

- Traces ellipsoïdes

L'équation générale d'une surface dans l'espace est f (x, y, z) = 0 et les traces de la surface sont les courbes:

Peut vous servir: magnitude vectorielle

- x = c; F (c, y, z) = 0

- y = c; F (x, c, z) = 0

- Z = c; F (x, y, c) = 0

Dans le cas d'un ellipsoïde, ces courbes sont des ellipses et parfois des circonférences.

- Volume

Le volume V de l'ellipsoïde est donné par (4/3) π fois le produit de ses trois moitié -semi:

V = (4/3) π. abc

Cas ellipsoïdes spéciaux

-Un ellipsoïde devient une sphère lorsque toutes les moitié sont de la même taille: a = b = c ≠ 0. Cela a du sens, car l'ellipsoïde est comme une sphère à laquelle elle a été étirée différemment dans chaque axe.

-Le sphéroïde est un ellipsoïde dans lequel deux des semi-jes sont identiques et le troisième est différent, par exemple, il pourrait être a = b ≠ c.

Le sphéroïde est également appelé révolution ellipsoïde, car il peut être généré par des ellipses rotatives autour d'un axe.

Si l'axe de virage coïncide avec l'axe majeur, le sphéroïde est producteur, Mais s'il coïncide avec l'axe mineur, c'est oblat:

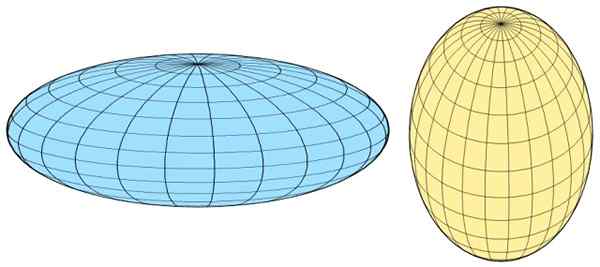figure 3. Sphéroïde gauche à gauche et prolution des sphéroïdes à droite. Source: Wikimedia Commons.

La mesure de l'aplatissement des sphéroïdes (ellipticité) est donnée par la différence de longueur entre les deux semi-pages, exprimée sous une forme fractionnaire, c'est-à-dire que c'est l'aplatissement de l'unité, donné par:

F = (a - b) / a

Dans cette équation, A représente le semi-Senije et B le semi-axe mineur, rappelez-vous que le troisième axe est égal à l'un d'eux pour un sphéroïde. La valeur de F est comprise entre 0 et 1 et pour un sphéroïde, il doit être supérieur à 0 (s'il était égal à 0, nous aurions simplement une sphère).

Peut vous servir: Bethelgeuse

L'ellipsoïde de référence

Les planètes et en général les étoiles ne sont généralement pas des sphères parfaites, car le mouvement de rotation autour de leurs haches plafonnant le corps dans les poteaux et les bassins de l'Équateur.

C'est pourquoi la terre se révèle être comme un sphéroïde oblat, mais pas aussi exagéré que celui de la figure précédente, et d'autre part, le géant gazeux de Saturne est le plus amer des planètes du système solaire.

Ainsi, une manière plus réaliste de représenter les planètes est de supposer qu'elles sont comme un sphéroïde ou un ellipsoïde de la révolution, dont le semi -semi est la radio équatoriale et le semi-axe mineur du rayon polaire.

Des mesures minutieuses prises sur le globe ont permis de construire le Référence ellipsoïde de la Terre comme sa forme la plus précise pour travailler mathématiquement.

Les étoiles ont également des mouvements de rotation qui leur donnent des formes plus ou moins aplaties. L'étoile rapide Aternar, la huitième étoile la plus brillante du ciel nocturne, dans la constellation sud d'Eridanus est remarquablement elliptique lors de la comparaison avec la majorité. Il est 144 années-lumière de nous.

À l'autre extrême, il y a quelques années, les scientifiques ont donné avec l'objet le plus sphérique que l'on trouve jusqu'à présent: l'étoile Kepler 11145123, 5000 années-lumière, avec une taille deux fois celle de notre soleil et une différence entre les semi-sesseurs de seulement 3 km. Comme prévu, il devient également plus lentement.

Quant à la Terre, ce n'est pas un sphéroïde parfait en raison de sa surface accidentée et des variations locales de gravité. C'est pourquoi il y a plus d'une sphéroïde de référence disponible et sur chaque site la plus appropriée à la géographie locale est choisie.

Il peut vous servir: quelle est la vallée en physique? (Avec des exemples)

L'aide des satellites est inestimable pour créer des modèles de plus en plus précis de la forme de la terre, grâce à eux, il est connu par exemple que le pôle Sud est plus proche de l'Équateur que le pôle Nord.

Figure 4. Haumea, la planète naine transneptunienne a une forme ellipsoïdale. Source: Wikimedia Commons.

Exemple numérique

En raison de la rotation de la terre, une force centrifuge est générée qui lui donne la forme d'un ellipsoïde oblongue, au lieu d'une sphère. Il est connu que la radio équatoriale de la Terre est de 3963 milles et que le rayon polaire est de 3942 miles.

Trouver l'équation de la trace équatoriale, celle de cet ellipsoïde et la mesure de son aplatissement. Comparez également avec l'ellipticité de Saturne, avec les données fournies ci-dessous:

-Radio équatoriale Saturne: 60268 km

-Radio polaire de Saturne: 54364 km

Solution

Un système de coordonnées est requis, que nous supposerons axé sur l'origine (centre de la terre). Nous supposerons que l'axe z vertical et la trace qui correspond à l'équateur se trouve sur le plan xy, équivalent au plan z = 0.

Dans le plan équatorial, les semi -a et b sont les mêmes, donc a = b = 3963 miles, tandis que c = 3942 miles. Ceci est un cas spécial: une sphéroïde axée sur le point (0,0,0) comme indiqué ci-dessus.

La trace équatoriale est un cercle de rayon r = 3963 miles, concentré sur l'origine. Il est calculé en faisant z = 0 dans l'équation standard:

Et l'équation standard de l'ellipsoïde de la Terre est:

Enfin, la mesure d'ajustement (elliptique) est calculée d'évaluation dans l'équation:

F _Atterrir = (a - b) / a = (3963-3942) miles / 3963 miles = 0.0053

F _Saturne = (60268-54363) km / 60268 km = 0.0980

Notez que l'elliptique F est un montant sans dimension.

Les références

1. Arcgis pour le bureau. Sphéroïdes et sphères. Récupéré de: bureau.Arcgis.com.
2. Monde de la BBC. Le mystère de l'objet le plus sphérique jamais découvert dans l'univers. Récupéré de: BBC.com.
3. Larson, R. Calcul et géométrie analytique. Sixième édition. 2ieme volume. McGraw Hill.
4. Wikipédia. Ellipsooïde. Récupéré de: dans.Wikipédia.org.
5. Wikipédia. Siperoïde. Récupéré de: dans.Wikipédia.org.