Équations polynomiques

Que sont les équations polynomiales?

Le Équations polynomiques Ils sont une déclaration qui augmente l'égalité de deux expressions ou membres, où au moins l'un des termes qui composent chaque côté de l'égalité sont les polynômes p (x). Ces équations sont nommées selon le degré de leurs variables.

En général, une équation est une déclaration qui établit l'égalité de deux expressions, où au moins une d'entre elles, il existe des quantités inconnues, qui sont appelées variables ou inconnues. Bien qu'il existe de nombreux types d'équations, celles-ci sont généralement classées en deux types: algébrique et transcendant.

Les équations polynomiques ne contiennent que des expressions algébriques, qui peuvent avoir une ou plusieurs inconnues qui interviennent dans l'équation. Selon l'exposant (grade) qu'ils ont, ils peuvent être classés comme: première année (linéaire), deuxième année (quadratique), troisième année (cubique), quatrième année (quant), de degré supérieur ou égal à cinq et irrationnel.

Caractéristiques des équations polynomiales

Les équations polynomiques sont des expressions formées par une égalité entre deux polynômes; C'est-à-dire pour les sommes finies de multiplications entre des valeurs qui sont inconnues (variables) et les nombres fixes (coefficients), où les variables peuvent avoir des exposants, et leur valeur peut être un entier positif, y compris zéro.

Les exposants déterminent le degré ou le type d'équation. Ce terme de l'expression qui a le plus de valeur exposant représentera le degré absolu de polynôme.

Les équations polynomiques sont également connues sous le nom d'algébrique, leurs coefficients peuvent être des nombres réels ou complexes et les variables sont des nombres inconnus représentés par une lettre, telle que: "x".

Si en remplaçant une valeur par la variable "x" dans p (x), le résultat est égal à zéro (0), alors il est dit que cette valeur satisfait l'équation (c'est une solution), et est généralement appelée racine polynomiale.

Lorsqu'une équation polynomiale est développée, toutes les racines ou solutions veulent être trouvées.

Types d'équations polynomiales

Il existe plusieurs types d'équations polynomiales, qui sont différenciées en fonction du nombre de variables, et également selon leur degré de leur exposant.

Ainsi, les équations polynomiales - où son premier terme est un polynôme qui n'a qu'un seul inconnu, étant donné que son degré peut être n'importe quel nombre naturel (n) et que le deuxième terme est nul - peut être exprimé comme suit:

Peut vous servir: Histoire de la trigonométrie de ses origines

pour_{N *} Xⁿ + pour_{N-1 *} X^N-1 +… + A_{1 *} X¹ + pour_{0 *} X₀ = 0

Où:

• pour_n, pour_N-1 déjà₀, Ce sont de vrais coefficients (nombres).
• pour_n est différent de zéro.
• L'exponte N est un entier positif qui représente le degré d'équation.
• x est la variable ou inconnue qui doit être recherchée.

Le degré absolu ou supérieur d'une équation polynomiale est cet exposant de plus grande valeur parmi tous ceux qui forment le polynôme; De cette façon, les équations sont classées comme:

Première année

Les équations polynomiales au premier degré, également appelées équations linéaires, sont celles à laquelle le degré (le plus grand exposant) est égal à 1, le polynôme est de la forme p (x) = 0; Et il est composé d'un terme linéaire et indépendant. Il est écrit comme suit:

ax + b = 0.

Où:

• a et b sont des nombres réels et a ≠ 0.
• La hache est le terme linéaire.
• B est le terme indépendant.

Par exemple, équation 13x - 18 = 4x.

Pour résoudre les équations linéaires, tous les termes contenant le X inconnu doivent être transmis sur le côté de l'égalité, et ceux qui ne se déplacent pas de l'autre côté, afin de l'effacer et d'obtenir une solution:

13x - 18 = 4x

13x = 4x + 18

13x - 4x = 18

9x = 18

x = 18 ÷ 9

x = 2.

De cette façon, l'équation donnée n'a qu'une seule solution ou racine, qui est x = 2.

Second grade

Les équations polynomiales au deuxième degré, également appelées équations quadratiques, sont celles dans lesquelles le degré (le plus grand exposant) est égal à 2, le polynôme est de la forme p (x) = 0, et est composé d'un terme quadratique, un linéaire et indépendant. Il est exprimé comme suit:

hache² + bx + c = 0.

Où:

• A, B et C sont des nombres réels et A ≠ 0.
• hache² C'est le terme quadratique, et "a" est le coefficient du terme quadratique.
• bx est le terme linéaire, et «b» est le coefficient du terme linéaire.
• C est le terme indépendant.

Résolvant

Généralement, la solution à ce type d'équations est donnée lors de la défrichement X de l'équation, et reste comme suit, qui est appelé résolvant:

Peut vous servir: théorème binomial

Là, (b² - 4AC) est appelé discrimination de l'équation et cette expression détermine le nombre de solutions que l'équation peut avoir:

• Oui B² - 4AC) = 0, l'équation aura une seule solution double; c'est-à-dire qu'il aura deux solutions égales.
• Oui B² - 4AC)> 0, l'équation aura deux solutions réelles différentes.
• Oui B² - 4AC) < 0, la ecuación no tiene solución (tendrá dos soluciones complejas distintas).

Par exemple, vous avez l'équation 4x² + 10x - 6 = 0, pour le résoudre d'abord les termes A, B et C sont identifiés, puis il est remplacé dans la formule:

A = 4

B = 10

C = -6.

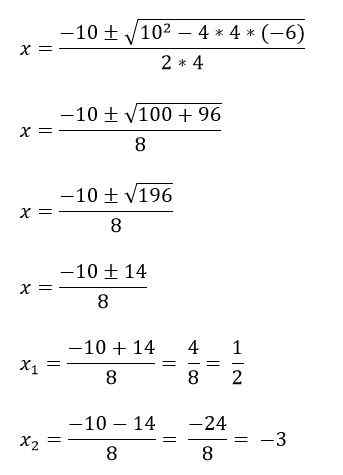
Il y a des cas dans lesquels les équations polynomiales de deuxième degrés n'ont pas les trois termes, et c'est pourquoi ils sont résolus différemment:

• Dans le cas où les équations quadratiques n'ont pas le terme linéaire (c'est-à-dire b = 0), l'équation sera exprimée en² + C = 0. Pour le résoudre, X est effacé² Et les racines carrées sont appliquées dans chaque membre, en se rappelant que les deux signes possibles que l'inconnu peut avoir:

hache² + C = 0.

X² = - c ÷ a

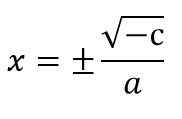
Par exemple, 5 x² - 20 = 0.

5 x² = 20

X² = 20 ÷ 5

x = ± √4

x = ± 2

X₁ = 2.

X₂ = -2.

• Lorsque l'équation quadratique n'a pas de terme indépendant (c'est-à-dire C = 0), l'équation sera exprimée en² + Bx = 0. Pour le résoudre, le facteur commun du X inconnu doit être pris dans le premier membre; Comme l'équation est appariée à zéro, il est réalisé qu'au moins l'un des facteurs sera égal à 0:

hache² + Bx = 0.

x (ax + b) = 0.

De cette façon, vous devez:

x = 0.

x = -b ÷ a.

Par exemple: vous avez l'équation 5x² + 30x = 0. C'est d'abord le facteur:

5x² + 30x = 0

x (5x + 30) = 0.

Deux facteurs sont générés qui sont x y (5x + 30). L'un d'eux sera considéré comme zéro et l'autre reçoit une solution:

X₁ = 0.

5x + 30 = 0

5x = -30

x = -30 ÷ 5

X₂ = -6.

Le niveau le plus élevé

Les équations polynomiales principales de degré sont celles qui vont de la troisième année, qui peuvent être exprimées ou résolues avec l'équation polynomiale générale pour tout degré:

Peut vous servir: coefficient de corrélation: formules, calcul, interprétation, exemple

pour_{N *} Xⁿ + pour_{N-1 *} X^N-1 +… + A_{1 *} X¹ + pour_{0 *} X₀ = 0

Ceci est utilisé parce qu'une équation avec un degré supérieur à deux est le résultat de la factorisation d'un polynôme; Autrement dit, il est exprimé comme la multiplication des polynômes de grade un ou plus, mais sans racines réelles.

La solution de ce type d'équations est directe, car la multiplication de deux facteurs sera égale à zéro si l'un des facteurs est nul (0); Par conséquent, chacune des équations polynomiales trouvées doit être résolue, correspondant à chacun de ses facteurs à zéro.

Par exemple, vous avez l'équation du troisième degré (cubique) x³ + X² +4x + 4 = 0. Pour le résoudre, vous devez suivre les étapes suivantes:

• Les termes sont groupés:

X³ + X² +4x + 4 = 0

(X³ + X² ) + (4x + 4) = 0.

• Les membres se décomposent pour obtenir le facteur commun de l'inconnu:

X² (x + 1) + 4 (x + 1) = 0

(X² + 4)_*(x + 1) = 0.

• De cette façon, deux facteurs sont obtenus, ce qui doit être égal à zéro:

(X² + 4) = 0

(x + 1) = 0.

• On peut voir que le facteur (x² + 4) = 0 n'aura pas de vraie solution, tandis que le facteur (x + 1) = 0 Oui. Par conséquent, la solution est:

(x + 1) = 0

x = -1.

Exercices résolus

Résolvez les équations suivantes:

Premier exercice

(2x² + 5)_*(X - 3)_*(1 + x) = 0.

Solution

Dans ce cas, l'équation est exprimée comme la multiplication des polynômes; c'est-à-dire qu'il est factorisé. Pour le résoudre, chaque facteur doit être égal à zéro:

2x² + 5 = 0, n'a pas de solution.

x - 3 = 0

x = 3.

1 + x = 0

x = - 1.

De cette façon, l'équation donnée a deux solutions: x = 3 et x = -1.

Deuxième exercice

X⁴ - 36 = 0.

Solution

Un polynôme a été donné, qui peut être résolu comme une différence de carrés pour atteindre une solution plus rapide. Ainsi, l'équation reste:

(X² + 6)_*(X² - 6) = 0.

Pour trouver la solution des équations, les deux facteurs sont égaux à zéro:

(X² + 6) = 0, n'a pas de solution.

(X² - 6) = 0

X² = 6

x = ± √6.

Ainsi, l'équation initiale a deux solutions:

x = √6.

x = - √6.