120 diviseurs

Les 120 diviseurs Ce sont tous ces chiffres qui le divisent exactement. Ces chiffres sont les suivants:

Diviseurs de 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 30, 40, 60, 120

Les opposés de cet ensemble de nombres, c'est-à-dire les négatifs, sont 120 diviseurs, car la division est exacte. Le 120 a 16 diviseurs entiers positifs et de nombreux autres négatifs.

Il existe plusieurs façons de trouver les diviseurs d'un nombre. Si ce n'est pas très grand, vous pouvez utiliser les tables de multiplication (pour les nombres moins de 100) et vérifier quelles tables le nombre en question apparaît. Par exemple, 12 apparaît dans les tableaux de 2, 3, 4 et 6, et ce sont leurs diviseurs, avec 1 et le même 12.

Le nombre peut également être décomposé en ses facteurs premiers, appliquer les règles de divisibilité et multiplier les facteurs. Mais il faut faire attention à ne pas passer un diviseur négligé.

Comme 120 est supérieur à 100, il n'est pas directement dans les tables de multiplication, cependant, il n'est pas trop laborieux pour trouver son 16. Une procédure valide pour tous les nombres est affichée immédiatement, grâce à l'utilisation de tables très simples.

Combien de diviseurs est 120?

Premièrement, le nombre de diviseurs de 120 est découvert. Il existe une formule qui vous permet de savoir combien vous en avez, bien qu'il ne dise pas ce qu'ils sont.

Les nombres composites, tels que 120, peuvent être exprimés comme le produit de nombres premiers, ou les pouvoirs de ceux-ci. Appel N à n'importe quel numéro de composé:

N = aⁿ ∙ B^m ∙ C^p … R^k

Peut vous servir: Relations de proportionnalité: concept, exemples et exercices

Les nombres a, b, c ... r sont des nombres premiers, et les valeurs de n, m, p, ... k, les pouvoirs respectifs. La décomposition des facteurs premiers de 120 est la suivante:

120 | 2
60 | 2
30 | 2
15 | 3
5 | 5
1 | 1

De cette façon, 120 est le produit des facteurs:

120 = 2³ ∙ 3 ∙ 5

Formule pour calculer le nombre de diviseurs de n

Nombre de diviseurs = (n +1) × (m +1) × (p +1)… × (k +1)

Maintenant, la formule à 120 est appliquée. De la décomposition des facteurs que vous devez:

n = 3 (est la puissance de 2)

M = 1 (le 3 est élevé à 1: 3¹ = 3)

P = 1 (le 5 semble également élevé à 1)

Avec ces valeurs:

Nombre de diviseurs de 120 = (3 +1) × (1 +1) × (1 +1) = 4 × 2 × 2 = 16

Ce résultat coïncide avec le début du début: 120 a 16 diviseurs. De plus, il est déjà connu que les 2, 3 et 5 sont des diviseurs de 120, ainsi que 10, car tout nombre terminé en 0 est divisible par 10. La procédure pour les trouver toutes est indiquée immédiatement.

Calcul des diviseurs de 120

Cela se fait à l'aide des facteurs calculés dans la section précédente. Là, il a été constaté que le 2 est un facteur de premier plan avec l'exposant 3, et le 3 est un autre facteur de cousin, avec l'exposant 1. Avec ces informations, le tableau suivant est construit:

Notez que les pouvoirs de 2 commencent en 2⁰ et se terminer par 2³, qui est le facteur qui survient lors de la décomposition de 120. Rappelez-vous que 2⁰ et 3⁰ Les deux sont égaux à 1 (n'importe quel nombre élevé à 0 est 1). Pour le facteur 3, il commence dans 3⁰ Jusqu'à 3¹, Depuis 3¹ = 3.

Ensuite, le tableau est complété avec le produit des nombres en rouge, comme indiqué ici:

Peut vous servir: inverse multiplicatif: explication, exemples, exercices résolus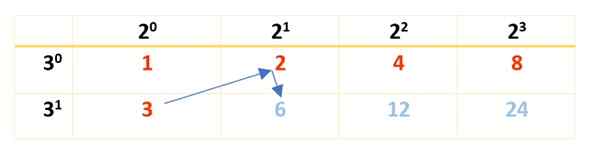

Tous les chiffres rouges et bleus sont à 120 diviseurs, mais il y en a à peine 8. Pour trouver les autres, un nouveau tableau est éclaté, les diviseurs déjà obtenus au premier rang et le facteur qui reste à prendre en compte est écrit: 5, avec leurs pouvoirs dans la première colonne, à gauche, comme ceci:

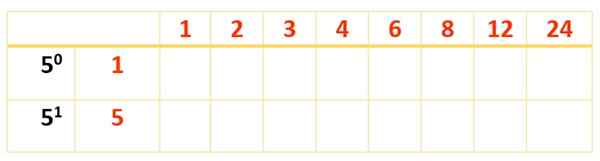
Maintenant, le tableau est complété avec les produits des chiffres en rouge, comme cela a été fait avec le premier tableau:

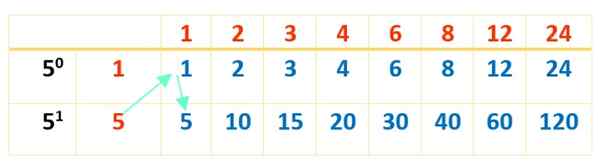
Et enfin les 16 diviseurs de 120 en bleu apparaissent. Les tables sont d'une excellente aide pour les opérations à effectuer dans l'ordre et donc pas de diviseur 120.

Exercices résolus

La procédure pour trouver tous les diviseurs d'un nombre est résumé comme suit:

1. Décomposer le nombre en facteurs premiers.
2. Calculez le nombre de diviseurs avec la formule.
3. Construisez les tables nécessaires pour trouver des diviseurs. Si le nombre a deux facteurs, un tableau suffit, si vous avez trois facteurs, deux tables doivent être faites, comme dans le cas de 120.

Exercice 1

Trouvez tous les diviseurs de 288.

Solution

288 se décompose en facteurs premiers:

288 | 2
144 | 2
72 | 2
36 | 2
18 | 2
9 | 3
3 | 3
1 | 1

Le 288 est écrit comme ceci:

288 = 2⁵ ∙ 3²

Est immédiatement le nombre de diviseurs de 288 à:

Nombre de diviseurs = (n +1) × (m +1) × (p +1)… × (k +1)

D'après la décomposition dans les facteurs premiers, il est noté que n = 5 et m = 2, alors:

Diviseurs de 288 = (5 +1) × (2 +1) = 6 × 3 = 18

Il y a 18 diviseurs et comme il n'y a que deux facteurs, il est suffisant avec un seul tableau:

Peut vous servir: caractéristiques du rectangle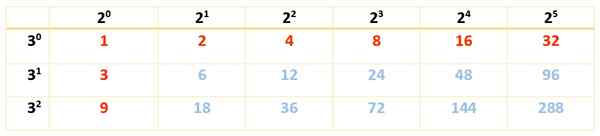

Les diviseurs de 288 sont les nombres en rouge et en bleu:

Div (288) = 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144, 288

Ils peuvent être vérifiés rapidement à l'aide d'une calculatrice.

Exercice 2

Trouvez les diviseurs de 350

Solution

350 Décompose:

350 | 2
175 | 5
35 | 5
7 | 7
1 | 1

Le 350 peut être écrit comme un produit de trois facteurs:

350 = 2 ∙ 5²∙ 7

L'étape suivante consiste à calculer le nombre de diviseurs, à travers la formule:

Nombre de diviseurs = (n +1) × (m +1) × (p +1)… × (k +1)

Avec n = 1, m = 2, p = 1

Diviseurs de 288 = (1 +1) × (2 +1) × (1 +1) = 2 × 3 × 2 = 12

Comme 350 nécessite trois facteurs, deux tables doivent être faites. Le premier se fait avec 2 et 5², Mais cela peut également être fait avec 2 et 7, ou avec 7 et 5², Selon la préférence, car sous toutes les formes, le résultat final est le même:

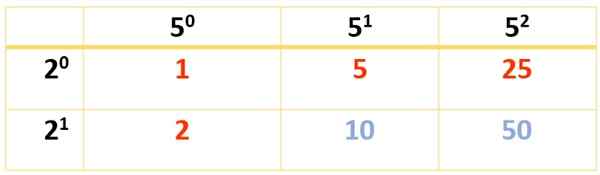
6 diviseurs sont obtenus. Les autres apparaissent à l'aide de cette autre table:

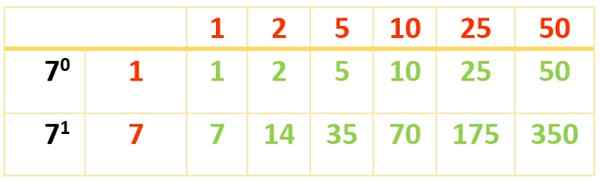
Les diviseurs de 350 sont:

Div (350) = 1, 2, 5, 7, 10, 14, 25, 35, 50, 70, 175, 350