Division synthétique

Nous expliquons ce qu'est la division synthétique, une méthode pour le faire, des exemples et des exercices résolus.

Qu'est-ce que la division synthétique?

La Division synthétique C'est un moyen simple de diviser un P (x) polynomial par l'un des formulaires d (x) = x - c - c. Par exemple, Polynôme P (x) = (x⁵+3x⁴-7x³+2x²-8x + 1) il peut être représenté comme la multiplication des deux polynômes les plus simples (x + 1) et (x⁴ + 2x³).

C'est un outil très utile, car, en plus de nous permettre de diviser les polynômes, il permet également d'évaluer un polynôme P (x) dans n'importe quel nombre C, qui à son tour nous indique précisément si ce nombre est un zéro ou non de la polynôme.

Grâce à l'algorithme de division, nous savons que si nous avons deux p (x) et d (x) polynôme (x) + r (x), où r (x) est nul ou est inférieur à Q (x). Ces polynômes sont connus sous le nom de quotient et de résidu ou de repos, respectivement.

Dans les occasions où le polynôme D (x) est de la forme x - c, la division synthétique nous donne un court moyen de trouver qui sont Q (x) et R (x).

Méthode de la division synthétique

Soit P (x) = A_nXⁿ+pour_N-1X^N-1+… + A₁x + a₀ le polynôme que nous voulons diviser et d (x) = x-c le diviseur. Pour diviser par la méthode de la division synthétique, nous procédons comme suit:

1- Nous écrivons les coefficients de P (x) dans la première ligne. Si une puissance X n'apparaît pas, nous plaçons zéro comme coefficient.

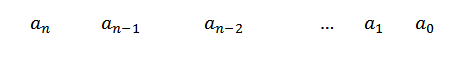
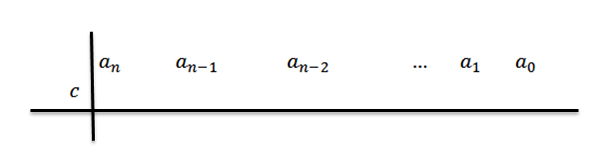
2- dans la deuxième rangée, à gauche d'un_n Nous placons C, et dessions des lignes de division, comme le montre la figure suivante:

3- Nous abaissons le coefficient principal à la troisième rangée.

Peut vous servir: méthode Euler: quelle est l'utilisation de la procédure et des exercices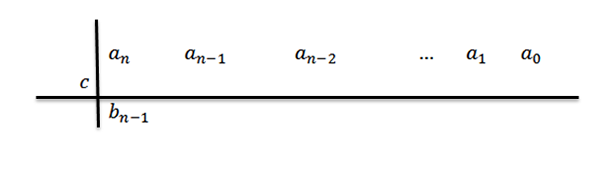

Dans cette expression b_N-1= A_n

4- Nous multiplions C par le coefficient principal b_N-1 Et nous écrivons le résultat dans la deuxième ligne, mais une colonne à droite.

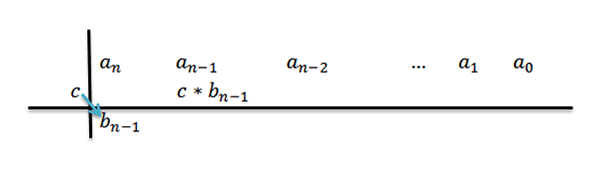
5- Nous ajoutons la colonne où nous écrivons le résultat précédent et le résultat est placé sous cette somme. C'est-à-dire dans la même colonne, troisième rangée.

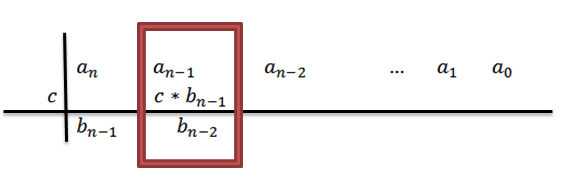
En ajoutant, nous avons en conséquence_N-1+c * b_N-1, à quoi pour le confort, nous appellerons b_N-2

6- Nous multiplions C par le résultat précédent et écrivons le résultat à votre droite dans la deuxième ligne.

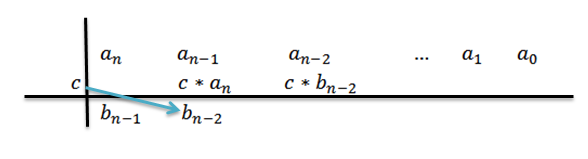
7- Nous répétons les étapes 5 et 6 jusqu'à ce que nous atteignions le coefficient à₀.

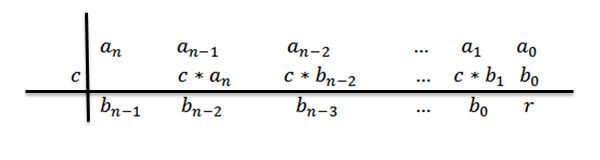
8- Nous écrivons la réponse, c'est-à-dire le quotient et le résidu. Comme nous faisons la division d'un polynôme de grade N entre un polynôme de grade 1, nous avons que le quotient serait grade N-1.

Les coefficients du polynôme du quotient seront le nombre de la troisième rangée, à l'exception du dernier, qui sera le polynôme résidu ou le reste de la division.

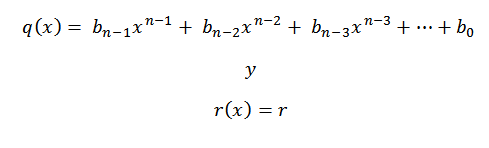
Exercices résolus

Exemple 1

Faire la division suivante par la méthode de la division synthétique:

(X⁵+3x⁴-7x³+2x²-8x + 1): (x + 1).

Solution

Nous écrivons d'abord les coefficients de dividende comme suit:

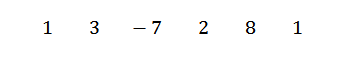
Ensuite, nous écrivons C sur le côté gauche, dans la deuxième rangée, ainsi que les lignes de division. Dans cet exemple C = -1.

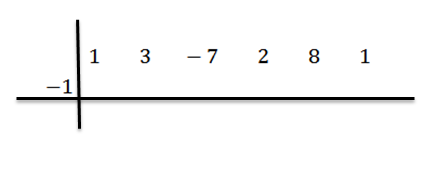
Nous abaissons le coefficient principal (dans ce cas b_N-1 = 1) et nous le multiplions par -1:

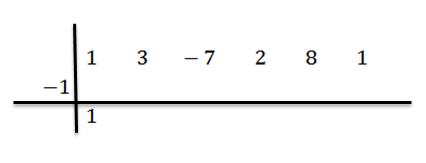
Nous avons écrit son résultat à droite dans la deuxième rangée, comme indiqué ci-dessous:

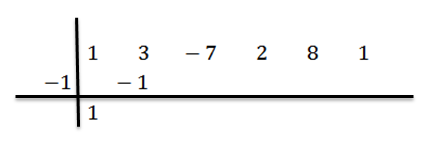
Nous ajoutons les numéros de la deuxième colonne:

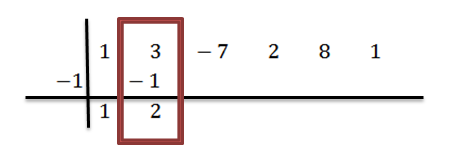
Nous multiplions 2 par -1 et écrivons le résultat dans la troisième colonne, deuxième ligne:

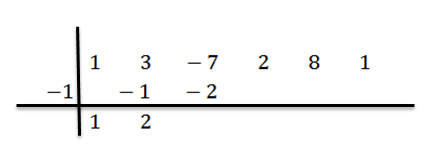
Nous ajoutons la troisième colonne:

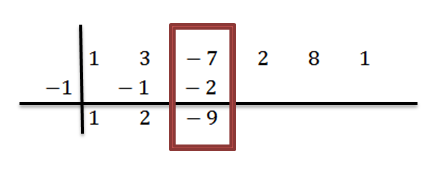
Nous procédons de manière analogue jusqu'à ce que nous atteignions la dernière colonne:

Peut vous servir: par défaut et approche excédentaire: quels sont et des exemples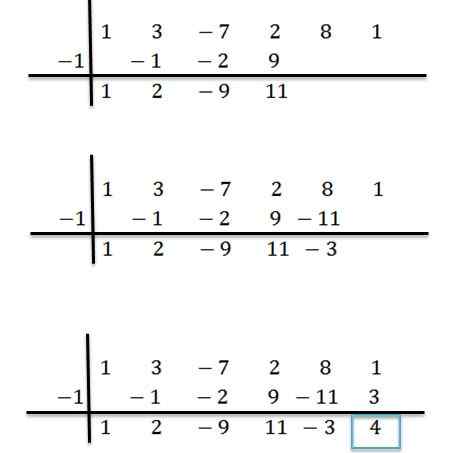

Ainsi, nous avons que le dernier nombre obtenu est le reste de la division, et les nombres restants sont les coefficients du quotient polynôme. Ceci est écrit comme suit:

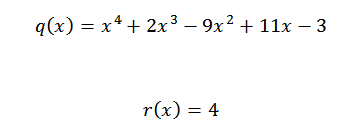
Si nous voulons vérifier que le résultat est correct, il suffit de vérifier que l'équation suivante est remplie:

P (x) = q (x) * d (x) + r (x)

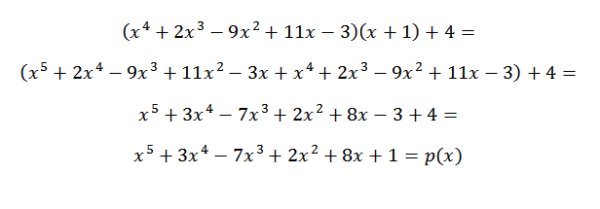
Ainsi, nous pouvons vérifier que le résultat obtenu est correct.

Exemple 2

Effectuer la division polynomiale suivante par la méthode de la division synthétique:

(7x³-x + 2): (x + 2)

Solution

Dans ce cas, nous avons que le terme x² Il n'apparaît pas, nous allons donc écrire à 0 comme coefficient. Ainsi, le polynôme resterait 7x³+0x²-x + 2.

Nous écrivons vos coefficients dans une ligne, c'est-à-dire:

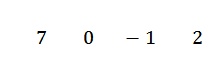
Nous écrivons la valeur de C = -2 sur le côté gauche dans la deuxième ligne et dessinez les lignes de division.

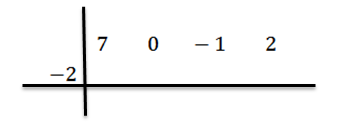
Nous abaissons le coefficient principal b_N-1 = 7 et nous le multiplions par -2, écrivant son résultat dans la deuxième ligne vers la droite.

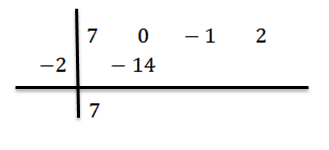
Nous ajoutons et procédons, comme expliqué précédemment, jusqu'à ce que nous atteignions le dernier terme:

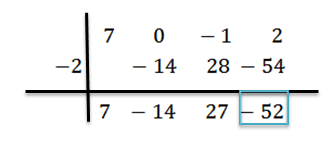
Dans ce cas, le reste est r (x) = -52 et le quotient obtenu est q (x) = 7x²-14x + 27.

Exemple 3

Une autre façon d'utiliser la division synthétique est la suivante.

Pour l'algorithme de division, nous pouvons écrire le polynôme P (x) comme suit:

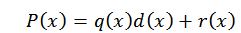
Dans cette expression, Q (x) et R (x) sont le quotient et le reste, respectivement. Maintenant, si d (x) = x-c, lors de l'évaluation en C en polynôme, nous trouvons ce qui suit:

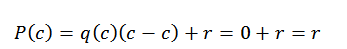
C'est pourquoi il ne reste que de trouver r (x), et nous pouvons le faire grâce à la division synthétique.

Par exemple, nous avons le polynôme P (x) = x⁷-9x⁶+19x⁵+12X⁴-3x³+19x²-37x-37 Et nous voulons savoir quelle est sa valeur lors de l'évaluation à x = 5. Pour cela, nous effectuons la division entre p (x) et d (x) = x -5 par la méthode de la division synthétique:

Peut vous servir: symétrie axiale: propriétés, exemples et exercices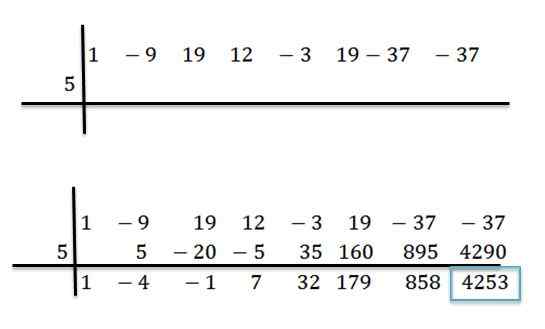

Une fois les opérations effectuées, nous savons que nous pouvons écrire P (x) comme suit:

P (x) = (x⁶-4x⁵ -X⁴+ 7x³ +32x² +179x + 858) * (X-5) + 4253

Par conséquent, lors de l'évaluation, nous devons:

P (5) = (5-4 (5) -5 + 7 (5) +32 (5) +179 (5) +858) * (5-5) +4253

P (5) = (5-4 (5) -5 + 7 (5) +32 (5) +179 (5) +858) * (0) +4253

P (5) = 0 + 4253 = 4253

Comme nous pouvons le voir, il est possible d'utiliser la division synthétique pour trouver la valeur d'un polynôme lors de l'évaluation en C au lieu de simplement remplacer C par x. 

Si nous essayons d'évaluer P (5) de la manière traditionnelle, nous aurions besoin de certains calculs qui deviennent généralement fastidieux.

Exemple 4

L'algorithme de division pour les polynômes est également atteint pour les polynômes avec des coefficients complexes et, par conséquent, nous avons que la méthode de division synthétique fonctionne également pour ces polynômes. Ensuite, nous verrons un exemple.

Nous utiliserons la méthode de la division synthétique pour montrer que z = 1+ 2i est un zéro du polynôme p (x) = x³+ (1 + i) x² -(1 + 2i) x + (15 + 5i). C'est-à-dire que le résidu de la division P (x) entre d (x) = x - z est égal à zéro.

Nous procédons comme avant: dans la première ligne, nous écrivons les coefficients de P (x), puis dans la seconde, nous écrivons z et dessinez les lignes de division.

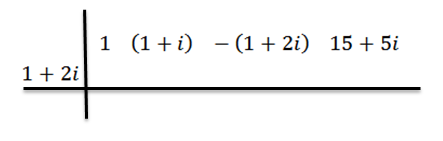
Nous faisons la division comme avant: c'est-à-dire:

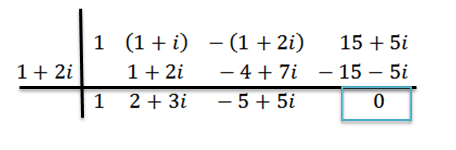
Nous pouvons voir que le résidu est nul; Par conséquent, nous concluons que z = 1+ 2i est un zéro de p (x).

Les références

1. Baldor, Aurelio. Algèbre. Groupe éditorial de Patria.
2. Demana, Waits, Foley & Kennedy. Preáculo: graphique, numérique, algébrique. Pearson Education.