Distribution f Caractéristiques et exercices résolus

La Distribution F o La distribution de Fisher-Snedecor est ce qui est utilisé pour comparer les variances de deux populations différentes ou indépendantes, chacune suit une distribution normale.

La distribution qui suit la variance d'un ensemble d'échantillons d'une seule population normale est la distribution du ji-carré (Χ²) de degré n-1, si chacun des échantillons de l'ensemble a n éléments.

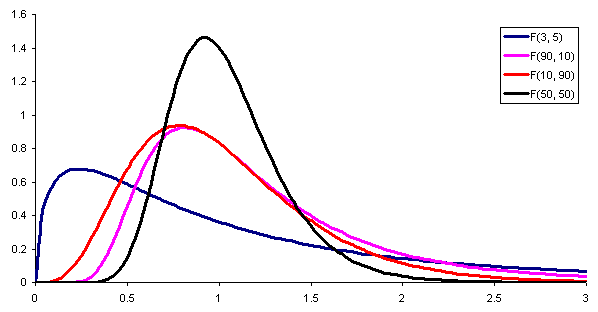
Figure 1. Voici la densité de probabilité de la distribution F avec différentes combinaisons de paramètres (ou degrés de liberté) du numérateur et du dénominateur respectivement. Source: Wikimedia Commons.

Pour comparer les variances de deux populations différentes, il est nécessaire de définir un statistique, c'est-à-dire une variable aléatoire auxiliaire qui permet de discerner si les deux populations ont ou non la même variance.

Cette variable auxiliaire peut être directement le quotient des variances d'échantillon de chaque population, auquel cas, si ledit quotient est proche de l'unité, il est en évidence que les deux populations ont des variances similaires.

[TOC]

La statistique F et sa distribution théorique

La variable aléatoire f ou statistique F proposée par Ronald Fisher (1890 - 1962) est celle utilisée plus fréquemment pour comparer les variances de deux populations et est définie comme suit:

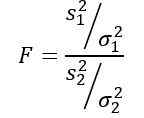
Être s² La variance de l'échantillon et σ² La variance de la population. Pour distinguer chacun des deux groupes de population, les abonnements 1 et 2 sont utilisés respectivement.

Il est connu que la distribution du Ji-Square avec (N-1) degrés de liberté est celle qui suit la variable auxiliaire (ou statistique) qui est définie ci-dessous:

X² = (N-1) s² / σ².

Par conséquent, la statistique F suit une distribution théorique donnée par la formule suivante:

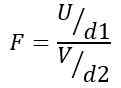
Être OU La distribution du ji-carré avec D1 = n1 - 1 degrés de liberté pour la population 1 et V La distribution du ji-carré avec D2 = n2 - 1 Degrés de liberté pour la population 2.

Peut vous servir: algèbre vectorielle

Le rapport défini de cette manière est une nouvelle distribution de probabilité, connue sous le nom Distribution F avec D1 degrés de liberté dans le numérateur et D2 degrés de liberté dans le dénominateur.

Moyen, mode et variance de la distribution f

Moitié

La distribution moyenne F est calculée comme suit:

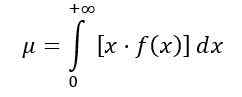
Étant f (x) la densité de probabilité de distribution f, qui est illustrée à la figure 1 pour plusieurs combinaisons de paramètres ou degrés de liberté.

Vous pouvez écrire la densité de probabilité F (x) en fonction de la fonction γ (fonction gamma):

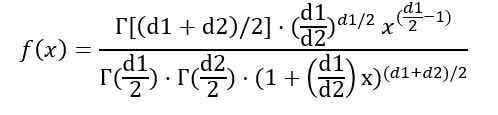
Une fois l'intégrale indiqué précédemment, il est conclu que la moyenne de la distribution F avec des degrés de liberté (D1, D2) est: est: est: est:

μ = d2 / (d2 - 2) avec d2> 2

Où cela montre que, curieusement, la moyenne ne dépend pas des degrés de liberté D1 du numérateur.

Mode

D'un autre côté, la mode dépend de D1 et D2 et est donnée par:

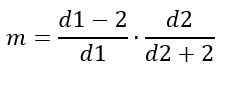
Pour d1> 2.

Variance de la distribution f

La variance σ² de la distribution f est calculée à partir de l'intégrale:

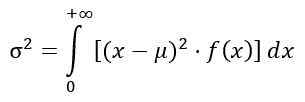
Obtention:

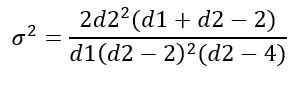
Gestion de la distribution F

Comme d'autres distributions de probabilité continue qui impliquent des fonctions complexes, la distribution F La gestion est effectuée par des tables ou par logiciel.

Tables de distribution F

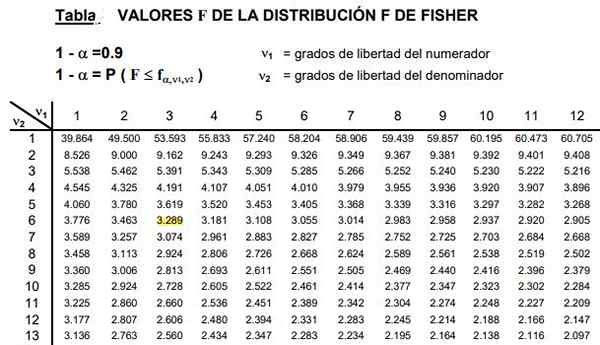Figure 2. Une partie du tableau de distribution F est indiquée, qui sont généralement très étendues car il existe une large combinaison de degrés de liberté possibles D1 et D2.

Les tableaux impliquent les deux paramètres ou degrés de liberté de distribution F, la colonne indique le degré de liberté du numérateur et le rang du degré de liberté du dénominateur.

Peut vous servir: inégalité du triangle: démonstration, exemples, exercices résolus

La figure 2 montre une section du tableau de distribution F pour le cas d'un niveau de signification 10%, c'est-à-dire α = 0,1. La valeur de f est mise en évidence lorsque d1 = 3 et d2 = 6 avec un niveau de confiance 1- α = 0,9 C'est 90%.

Logiciel de distribution F

Quant au logiciel qui gère la distribution F, il existe une grande variété, des feuilles de calcul comme Exceller même des packages spécialisés tels que Minitab, SPSS et R Pour nommer certains des plus connus.

Il convient de noter que les logiciels de géométrie et de mathématiques Géogebra Il a un outil statistique qui comprend les principales distributions, y compris la distribution F. La figure 3 montre la distribution F pour le cas d1 = 3 et d2 = 6 un niveau de confiance 90%.

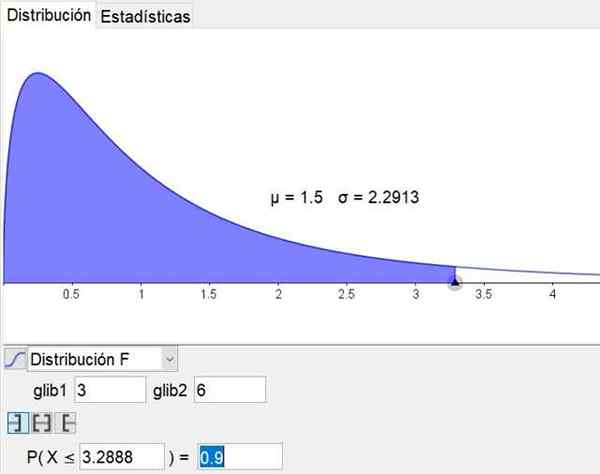figure 3. La distribution F est indiquée pour le cas D1 = 3 et D2 = 6 avec un niveau de confiance à 90%, obtenu via l'outil statistique Geogebra. Source: Geogebra.org

Exercices résolus

Exercice 1

Considérez deux échantillons de populations qui ont la même variance de population. Si l'échantillon 1 est de taille n1 = 5 et que l'échantillon 2 est de taille n2 = 10, déterminez la probabilité théorique que le rapport de ses variances respectives est inférieure ou égale à 2.

Solution

Il faut se rappeler que la statistique F est définie comme:

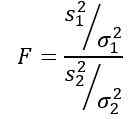
Mais on nous dit que les écarts de population sont les mêmes, donc pour cet exercice, cela s'applique:

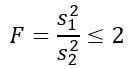
Comme vous voulez connaître la probabilité théorique que ce rapport des variances d'échantillon est inférieur ou égal à 2, nous devons connaître la zone sous la distribution F entre 0 et 2, qui peut être obtenue par des tables ou des logiciels. Pour cela, il faut tenir compte du fait que la distribution requise f a d1 = n1 - 1 = 5 - 1 = 4 et d2 = n2 - 1 = 10 - 1 = 9, c'est-à-dire la distribution F avec des degrés de liberté (4, 9).

Il peut vous servir: série de puissance: exemples et exercices

En utilisant l'outil statistique de Géogebra Il a été déterminé que cette zone est 0.82, il est donc conclu que la probabilité que le rapport des variances d'échantillon soit inférieur ou égal à 2 est de 82%.

Exercer 2

Il y a deux processus de fabrication de feuilles minces. La variabilité de l'épaisseur doit être autant que possible. 21 échantillons de chaque processus sont prélevés. L'échantillon de processus a un écart-type de 1,96 microns, tandis que celui du processus B a un écart-type de 2,13 microns. Lequel des processus a une variabilité plus faible? Utilisez un niveau de rejet de 5%.

Solution

Les données sont les suivantes: SB = 2,13 avec NB = 21; SA = 1,96 avec Na = 21. Cela signifie que vous devez travailler avec une distribution F de (20, 20) degrés de liberté.

L'hypothèse nulle implique que la variance de la population des deux processus est identique, c'est-à-dire σa ^ 2 / σb ^ 2 = 1. L'hypothèse alternative impliquerait différentes variances de population.

Ensuite, sous l'hypothèse de variances de population identiques, la statistique f calculée comme: fc = (sb / sa) ^ 2 est définie.

Comme le niveau de rejet a été considéré comme α = 0,05, alors α / 2 = 0,025

La distribution f (0.025; 20,20) = 0,406, tandis que f (0.975; 20,20) = 2,46.

Par conséquent, l'hypothèse nulle sera vraie si le F calculé est conforme: 0,406≤fc≤2,46. Sinon l'hypothèse nulle est rejetée.

Comme fc = (2,13 / 1,96) ^ 2 = 1,18, il est conclu que la statistique FC se trouve dans la plage d'acceptation de l'hypothèse nulle avec une certitude de 95%. En d'autres termes, avec une certitude de 95%, les deux processus de fabrication ont la même variance de population.

Les références

1. F test pour l'indépendance. Récupéré de: saylordotorg.Github.Io.
2. Vague de médicaments. Statistiques appliquées aux sciences de la santé: test F. Récupéré de: medwave.CL.
3. Probabilités et statistiques. Distribution F. Récupéré de: Probabilités etstics.com.
4. Triola, m. 2012. Statistiques élémentaires. 11ème. Édition. Addison Wesley.
5. Unam. Distribution F. Récupéré de: Advisory.Cuautitlan2.Unam.mx.
6. Wikipédia. Distribution F. Récupéré de: est.Wikipédia.com