Dynamique des exemples de système de particules, exercices

La Dynamique d'un système de particules Il consiste en l'application des lois de Newton du mouvement à un ensemble de particules, qui peuvent être discrètes (les particules peuvent être comptées) ou pour faire partie d'un objet étendu, dans ce cas, le système est continu.

Pour expliquer le mouvement d'un système de particules, il est gênant d'analyser chacun séparément et de voir quelles forces agissent dessus. Au lieu de cela, un point représentatif de l'ensemble est défini, appelé Centre de masse.

Décrire le mouvement du centre de masse offre un panorama très réussi du mouvement mondial de l'ensemble, permet également d'appliquer les lois de Newton analogues au moment où l'objet est considéré comme une particule sans dimensions.

Ce dernier modèle, appelé modèle de particules, Il est bon de décrire les traductions et aussi lorsqu'il n'est pas nécessaire de considérer les dimensions de l'objet. Mais les objets ordinaires sont de taille et s'ils ont également un mouvement de rotation, il est nécessaire de prendre en compte les points sur lesquels les forces sont appliquées.

[TOC]

Exemples

La terre et la lune

Illustration de la Terre et de la Lune

Un ensemble de particules discrètes m₁, m₂, m₃... qui finit par se déplacer par rapport à l'origine d'un système de coordonnées, en raison de certaines force qui en résulte qui agissent sur eux est un bon exemple de système de particules.

La Terre peut être considérée comme une particule et la lune une autre, alors les deux constituent un système de 2 particules sous l'action de la force de gravité du soleil.

Objets étendus

Une personne, un animal ou tout objet de l'environnement, peut également être considérée comme un système de particules, seulement que celles-ci sont si petites, que l'on ne peut pas compter un par un. Il s'agit d'un système continu, mais en tenant compte de certaines considérations, son traitement est le même que pour un système discret.

Il peut vous servir: quelle est l'enthalpie de formation? (Avec des exercices)

Voici les détails.

Le centre de masse d'un système de particules

Pour démarrer l'étude d'un système de particules, vous devez trouver le centre de masse (CM), qui est le point où la masse entière du système est concentrée.

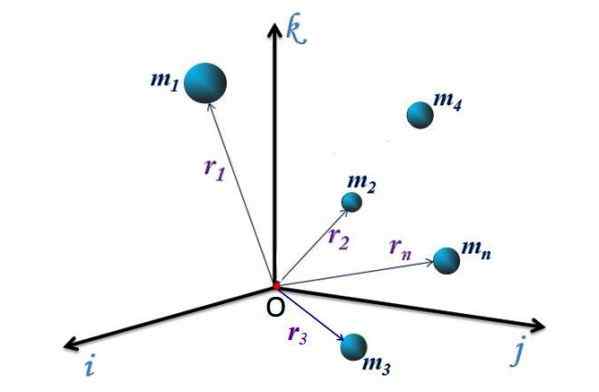
Figure 1. Un système de particules dans le système de référence XYZ. Source: F. Zapata.

Pour le système discret de la figure 1, avec n Particules, chacun a un vecteur de position dirigé à partir du système d'origine ou de coordonnées au point P (x, y, z) où la particule est. Ces vecteurs sont désignés comme r₁, r₂, r₃.. r_n.

Les coordonnées CM sont calculées par les équations suivantes:

Où chacune des masses de l'ensemble est représentée comme m₁, m₂, m₃... M_n. Notez que la somme ∑ m_Toi Il équivaut à la masse totale m de l'ensemble. Si le système est continu, les résumés sont remplacés par des intégrales.

Chacune des adresses perpendiculaires est représentée par les vecteurs unitaires Toi, J et k, Par conséquent, le vecteur de position CM, indiqué r_Cm, Il peut être exprimé par:

r_Cm = x_Cm Toi + et_Cm J + z_Cm k

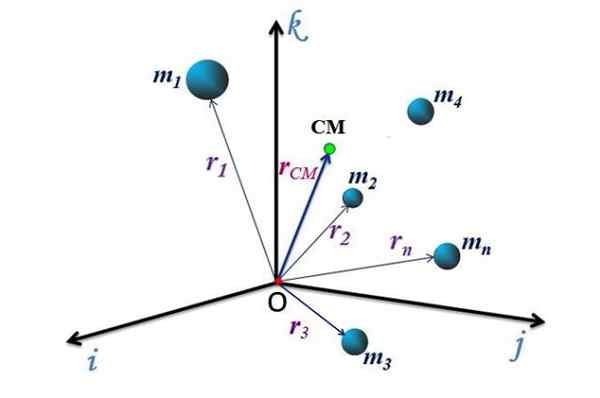Figure 2. Emplacement du centre de masse d'un système de particules. Source: F. Zapata.

Mouvement CM

Une fois l'emplacement du centre de masse connu, les équations connues du mouvement sont appliquées. La vitesse de CM est la première dérivée de la position par rapport au temps:

Dans ce cas, le système a une quantité totale de mouvement P qui est calculé comme le produit de la masse totale du système et la vitesse du centre de masse:

Il peut vous servir: trajectoire physique: caractéristiques, types, exemples et exercices

P = M ∙V_Cm

Alternativement, la quantité totale du système du système peut être calculée directement:

P = m₁V₁ + m₂V₂ + m₃V₃ +.. . = ∑ m_Toi V_Toi

Tandis que l'accélération de CM est la vitesse dérivée:

Force sur CM

Les forces agissant sur un système de particules peuvent être:

• Forces internes, en raison des interactions entre les mêmes particules.
• Forces externes, causées par des agents externes au système.

Comme les forces internes sont présentées par des paires, de la même ampleur et de la même direction, mais les sens opposés, selon la troisième loi de Newton, il est réalisé que:

∑ F_int = 0

Par conséquent, les forces internes ne modifient pas le mouvement de l'ensemble, mais elles sont très importantes pour déterminer l'énergie interne.

Si le système est isolé et qu'il n'y a pas de forces externes, selon la première loi de Newton, le centre de masse est au repos ou se déplace avec un mouvement rectiligne uniforme. Sinon, le centre de masse connaît une accélération donnée par:

∑ F_ext = M ∙pour_Cm

Où m est la masse totale du système. L'équation précédente peut être écrite comme ceci:

Et cela signifie que la force externe équivaut à la variation temporaire de la quantité de mouvement, une autre façon d'exprimer la deuxième loi de Newton et la même utilisée par le célèbre physicien anglais dans son livre Principe.

Exercice résolu

Le centre de masse d'un système de 2 particules est sur l'axe x à un certain moment, en position x = 2.0 m et se déplaçant avec la vitesse 5.0 m / s dans la même direction et positivement. Si l'une des particules est à l'origine et l'autre, de masse 0.1 kg, est au repos à x = 8.0 m, calculer:

Peut vous servir: diamagnétisme: matériaux, applications, exemples

a) La masse de la particule qui est à l'origine.

b) quantité de mouvement du système

c) Quelle vitesse est la particule qui est à l'origine?

Solution à

De l'équation de la position du centre de masse:

r_Cm = x_Cm Toi + et_Cm J + z_Cm K = 2.0 m Toi

Comme le CM a une coordonnée X uniquement, la première équation de trio précédemment donnée est utilisée:

Les coordonnées sont désormais remplacées, si la particule est indiquée à l'origine telle que le numéro 1 et l'autre tel que le numéro 2, les données numériques sont:

X₁ = 0 m, x₂ = 8.0 m, m₂ = 0.1 kg, x_Cm = 2.0 m

Rester:

= 0.3 kg

Solution B

La quantité de mouvement du système est calculée par:

P = M ∙V_Cm

La masse totale m est égale à:

M = 0.3 kg + 0.1 kg = 0.4 kg

Donc:

P = 0.4 kg ∙ 5.0 m / s Toi = 2 kg.SP Toi

Solution C

De l'équation pour P d'un système à deux parties, il efface V₁, Étant donné que les autres données sont connues, car la déclaration indique que la particule 2 est donc au repos:

V₂ = 0 

ET P C'est simplement comme:

P = m₁V₁

V₁ = P / m₁ = 2 kg.SP Toi / 0.3 kg = 6.67 m / s Toi

Les références

1. université de Duke. Systèmes de particules. Récupéré de: webhome.Phy.Duc.Édu.
2. Rex, un. 2011. Fondamentaux de la physique. Pearson.
3. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. Volume 1. Pearson.
4. SERAY, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7e. Élégant. Cengage Learning.
5. Tipler, P. (2006) Physique de science et de technologie. 5e ed. Volume 1. Éditorial Revered.