Différence de formules, équations, exemples, exercices

La Différence de cubes C'est une expression algébrique binomiale de la forme à³ - b³, où les termes A et B peuvent être des nombres réels ou des expressions algébriques de divers types. Un exemple de différence de cubes est: 8 - x³, Puisque 8 peut être écrit comme 2³.

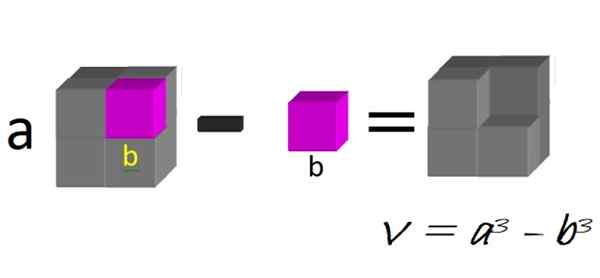
Géométriquement, nous pouvons penser à un grand cube, du côté A, auquel la petite boutique du côté B est soustraite, comme illustré à la figure 1:

Figure 1. Une différence de cubes. Source: F. Zapata.

Le volume de la figure résultante est précisément une différence de cubes:

V = a³ - b³

Pour trouver une expression alternative, il est observé que cette figure peut être décomposée en trois prismes, comme indiqué ci-dessous:

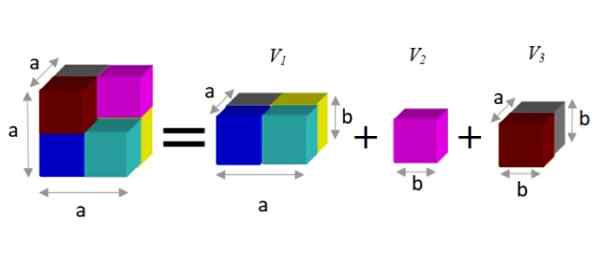Figure 2. La différence de cubes (à gauche de l'égalité) est égale à la somme des volumes partiels (à droite). Source: F. Zapata.

Un prisme a un volume donné par le produit de ses trois dimensions: Largeur x Haute profondeur. De cette façon, le volume résultant est:

V = a³ - b³ = A².b + b³ + pour.b²

Le facteur b C'est commun à droite. De plus, dans la figure illustrée ci-dessus, elle est en particulier que:

b = (a / 2) ⇒ a = b + b

Par conséquent, on peut dire que: b = a - b. De cette façon:

pour³ - b³ = B (a² + b² +pour.b) = (a-b) (a² + pour.b + b²)

Cette façon d'exprimer la différence de cubes s'avérera très utile dans de nombreuses applications et aurait été obtenue de la même manière, bien que le côté cube manquant dans le coin était différent de B = a / 2.

Notez que la deuxième parenthèseIl ressemble beaucoup au produit remarquable du carré de la somme, mais le terme croisé n'est pas multiplié par 2. Le lecteur peut développer le côté droit pour vérifier qu'il est effectivement obtenu pour³ - b³.

[TOC]

Peut vous servir: Binomial carré

Exemples

Il existe plusieurs différences de cubes:

1 - M⁶

pour⁶b³ - 8Z¹²et⁶

(1/125).X⁶ - 27.et⁹

Associons chacun d'eux. Dans le premier exemple, le 1 peut être écrit 1 = 1³ et le terme m⁶ Il reste: (m²)³. Les deux termes sont des cubes parfaits, donc leur différence est:

1 -m⁶ = 1³ - (m²)³

Dans le deuxième exemple, les termes sont réécrits:

pour⁶b³ = (a²b)³

8Z¹²et⁶ = 2³ (Z⁴)³ (et²)³ = (2Z⁴et²)³

La différence de ces cubes est: (A²b)³ - (2Z⁴et²)³.

Enfin, la fraction (1/125) est (1/5³), X⁶ = (x²)³, 27 = 3³ et et⁹ = (et³)³. Remplacement de tout cela dans l'expression originale, il est obtenu:

(1/125).X⁶  - 27 ans⁹ = [(1/5) (x²)]³ - (3 ans³)³

Factorisation d'une différence de cubes

FAIT La différence de cubes simplifie de nombreuses opérations algébriques. Pour ce faire, il suffit d'utiliser la formule déduite précédemment:

figure 3. Factorisation de la différence de cubes et expression d'un quotient remarquable. Source: F. Zapata.

Maintenant, la procédure pour appliquer cette formule se compose de trois étapes:

- Premièrement, la racine cubique de chacun des termes de la différence est obtenue.

- Ensuite, le binôme et le trinôme qui apparaissent sur le côté droit de la formule sont construits.

- Enfin, le binomial et le trinomial sont remplacés pour obtenir la factorisation finale.

Nous illustrerons l'utilisation de ces étapes avec chacun des exemples de différence de cubes proposés ci-dessus et donc obtenir son équivalent factoriel.

Exemple 1

Expression factive 1 -M⁶   Après les étapes décrites. Nous commençons par réécrire l'expression comme 1 -M⁶ = 1³ - (m²)³ Pour extraire les racines cubiques respectives de chaque terme:

Ensuite, le binôme et le trinôme sont construits:

Il peut vous servir: Théorie de la file d'attente: histoire, modèle, à quoi sert-il pour et des exemples pour

A = 1

b = m²

Ensuite:

A - b = 1 - m²

 (pour² +pour.b + b²) = 1² + 1.m² + (m²)² = 1 + m² + m⁴

 Enfin, il est remplacé dans la formule A³ - b³ = (a-b) (a² +pour.b + b²):

1 -m⁶ = (1 - m²) (1 + m² + m⁴)

Exemple 2

Factoriser:

pour⁶b³ -8Z¹²et⁶ = (a²b)³ - (2Z⁴et²)³

Comme ce sont des cubes parfaits, les racines cubiques sont immédiates: un²B et 2Z⁴et², De là, il s'ensuit:

- Binôme: A²B - 2Z⁴et²

- Trinomial: (un²b)² + pour²b. 2Z⁴et² + (pour²B + 2Z⁴et²)²

 Et maintenant, la factorisation souhaitée est construite:

pour⁶b³ -8Z¹²et⁶ = (a²B - 2Z⁴et²). [(pour²b)² + pour²b. 2Z⁴et² + (pour²B + 2Z⁴et²)²] =

= (a²B - 2Z⁴et²). [pour⁴b² + 2e²b.z⁴et² + (pour²B + 2Z⁴et²)²]]

En principe, la factorisation est prête, mais il est souvent nécessaire de simplifier chaque terme. Ensuite, le produit remarquable est développé à partir d'une somme - qui apparaît à la fin puis ajoute des termes similaires. Rappelant que le carré d'une somme est:

(x + y)² = x² + 2xy + et²

Le droit notable vers la droite se développe de cette manière:

(pour²B + 2Z⁴et²)² = A⁴b² + 4e²b.z⁴et² + 4Z⁸et⁴

 Remplacement du développement obtenu dans la factorisation de la différence de cubes:

pour⁶b³ -8Z¹²et⁶ = (a²B - 2Z⁴et²). [pour⁴b² + 2e²b.z⁴et² + pour⁴b² + 4e²b.z⁴et² + 4Z⁸et⁴] =

Enfin, regrouper des termes similaires et prise en compte des coefficients numériques, qui sont tous des paires, il est obtenu:

(pour²B - 2Z⁴et²). [2e⁴b² + 6e²b.z⁴et² + 4Z⁸et⁴] = 2 (A²B - 2Z⁴et²). [pour⁴b² + 3e²b.z⁴et² + 2Z⁸et⁴]]

Exemple 3

Factoriser (1/125).X⁶  - 27 ans⁹ C'est beaucoup plus simple que le cas précédent. Les équivalents de A et B sont d'abord identifiés:

A = (1/5) x²

B = 3y³

Ensuite, ils sont remplacés directement sur la formule:

(1/125).X⁶  - 27 ans⁹ = [(1/5) x² - 3Y³]]. [(1/25) x⁴ + (3/5) x²et³ + 9Y⁶]]

Exercice résolu

La différence de cubes a, comme nous l'avons dit, une variété d'applications en algèbre. Regardons certains:

Peut vous servir: 5 caractéristiques du plan cartésien

Exercice 1

Résolvez les équations suivantes:

a) x⁵ - 125 x² = 0

b) 64 - 729 x³ = 0

Solution à

L'équation est d'abord facteur de cette manière:

X² (X³ - 125) = 0

Comme 125 est un cube parfait, les parenthèses sont écrites comme une différence dans les cubes:

X² . (X³ - 5³) = 0

La première solution est x = 0, mais nous en trouvons plus si nous fabriquons x³ - 5³ = 0, alors:

X³ = 5³ → x = 5

Solution B

Le côté gauche de l'équation est réécrit comme 64 - 729 x³ = 4³ - (9x)³. Donc:

4³ - (9x)³ = 0

Puisque l'exposant est le même:

9x = 4 → x = 9/4

Exercice 2

Factoriser l'expression:

(x + y)³ - (X - y)³

Solution

Cette expression est une différence de cubes, si dans la formule de factorisation, nous remarquons que:

A = x + et

b = x- y

Ensuite, le binôme est construit en premier:

a - b = x + y - (x- y) = 2y

Et maintenant le trinomial:

pour² + pour.b + b² = (x + y)² + (x + y) (x-y) + (x-y)²

Des produits notables sont développés:

(x + y)² = x² + 2xy + et²

(x + y) (x-y) = x²- et²

(x- y)² = x² - 2xy + et²

Ensuite, vous devez remplacer et réduire les termes similaires:

pour² + pour.b + b² = x² + 2xy + et²+ X²- et²+ X² - 2xy + et² = 3x² + et²

La factorisation entraîne:

(x + y)³ - (X - y)³ = 2Y. (3x² + et²)

Les références

1. Baldor, un. 1974. Algèbre. Éditorial culturel vénézuélien s.POUR.
2. Fondation CK-12. Somme et différence de cubes. Récupéré de: CK12.org.
3. Académie Khan. Facteur de différence de cubes. Récupéré de: est.Khanacademy.org.
4. Les mathématiques sont amusantes. Différence de deux cubes. Récupéré de: Mathsisfun.com
5. Unam. Factorisation d'une différence de cubes. Récupéré de: DCB.Fi-c.Unam.mx.