Déplacement angulaire

Qu'est-ce que le déplacement angulaire?

Il Déplacement angulaire C'est le changement ou la variation de la position angulaire qu'un objet en rotation expériences, généralement mesuré en radians ou toute autre mesure donnée pour les virages, tels que les notes ou les révolutions.

Lorsqu'un objet tourne autour d'un axe fixe, son déplacement angulaire est déterminé en mesurant l'angle balayé par une ligne qui passe par n'importe quel point du corps croisant l'axe de rotation, c'est-à-dire une ligne radiale.

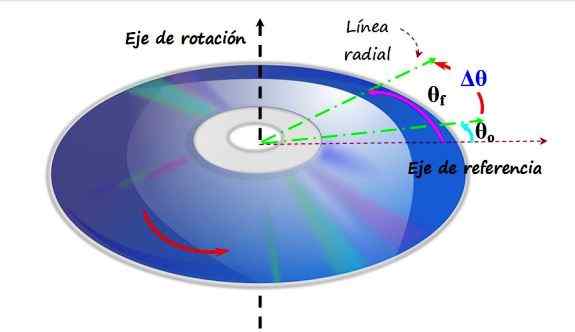Un disque ou CD compact tourne dans une direction antihorante autour d'un axe de rotation vertical. En passant de l'angle θo à θf, il est dit qu'il a connu un déplacement angulaire. Source: F. Zapata.

Dans la figure supérieure, il y a un CD qui tourne dans une direction anti-respect, étant son axe de rotation l'axe vertical. Un axe de référence est placé sur le plan du CD, qui correspond à l'angle 0 radians ou 0. La ligne verte est une ligne radiale, qui forme initialement un angle θ_soit Avec la référence. C'est votre position initiale.

Plus tard, la ligne verte se déplace vers une nouvelle position appelée θ_F, Et l'expérience expérimentée, appelée Δθ est simplement:

Δθ = θ_F - θ_soit

Tout point P du CD subit le même déplacement angulaire dans un certain intervalle de temps, à l'exception du centre, qui est l'endroit où l'axe de rotation passe et reste au repos.

Formules et équations

Il y a un objet qui tourne autour d'un axe fixe ou qui laisse l'écran au lecteur. Et à l'intérieur, il y a le point P, situé à une distance R de l'axe de rotation et décrivant les circonférences radio.

Ceci est vu dans la figure suivante, qui montre un objet de coupe, vu contraire aux aiguilles d'horloge. Le point en question est en position angulaire θ, mesurée à partir de l'axe de référence, qui dans ce cas est l'axe horizontal.

Peut vous servir: principe additif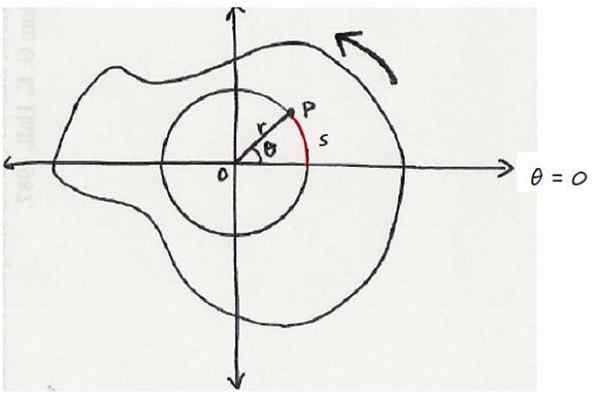Un objet qui tourne dans un sens anti-horaire. L'axe de rotation sort perpendiculaire à l'écran. Source: Wikimedia Commons.

Par convention, à la rotation au sens antihorarial, il se voit attribuer un sens positif, tandis que la rotation dans un calendrier a un signe négatif.

Comme le point P jure l'angle θ, il parcourt simultanément l'arc s. Comme θ est un angle central, puisque son sommet occupe le centre de la circonférence, il est réalisé que:

Avec θ exprimé en rayons.

Le déplacement angulaire est:

Δθ = θ_final  - θ_initial

Par exemple, si P a commencé avec θ_initial = 0 rad et ensuite est en θ_final = 0.8 rad, son déplacement angulaire est de:

Δθ = 0.8 rad - 0 rad =  0.8 rad

D'autres points de l'objet peuvent occuper différentes positions angulaires, mais toutes connaissent le même déplacement angulaire. Cependant, les particules les plus éloignées du centre parcourent les plus grandes distances, puisque s = r⋅θ.

Angles Mesure

Dans la rotation, il est courant de trouver les angles mesurés en radians, mais ils se trouvent également en degrés et révolutions ou virages. Dans la résolution de problèmes, il est nécessaire de passer de ces unités à Radianes.

1 Révolution est équivalente à un tour complet, c'est-à-dire lorsqu'un virage complet s'est cassé, il a tourné à 360 º et ceux-ci équivalent à 2π radians, car dans ce cas, le point a visité un arc égal à 2πr:

Mais simplifiant, l'équivalence précédente peut être exprimée comme suit:

π rayons = 180º

Comment le déplacement angulaire est-il calculé?

Le déplacement angulaire peut être calculé de manière analogue à la façon dont le déplacement du mouvement est calculé dans une dimension, suivant un certain modèle de mouvement. Pour cela, la vitesse angulaire moyenne est définie comme le déplacement angulaire Δθ dans un intervalle de temps donné ΔT:

Où la vitesse angulaire moyenne est indiquée comme ω_m et est donné en radians / s en unités du système international si.

Peut vous servir: comment obtenir l'angle d'un triangle? (Exemple)

La vitesse angulaire instantanée est la limite de la vitesse angulaire moyenne lorsque ΔT → 0:

C'est-à-dire qu'il est le premier dérivé de la position angulaire par rapport au temps. À son tour, une accélération angulaire peut être définie, désignée comme α, ce qui équivaut à la dérivée ou au taux de changement de vitesse angulaire par rapport au temps:

Qui peut également être interprété comme le second dérivé de la position angulaire par rapport au temps.

L'important est que deux modèles de mouvement peuvent être établis par analogie avec les mouvements rectilignes, car bien que les rotations soient effectuées dans le plan, une seule coordonnée angulaire est suffisante pour établir la position de n'importe quel point de l'objet.

Mouvement circulaire uniforme

Dans le mouvement circulaire uniforme, la vitesse angulaire est constante, c'est-à-dire que la vitesse angulaire moyenne est égale à la vitesse angulaire instantanée. Comme l'accélération angulaire α est égale à 0, vous pouvez écrire l'équation suivante pour la position en fonction du temps:

θ = θ_soit + Ωt

Où θ_soit C'est la position initiale du mobile.

Mouvement circulaire uniformément accéléré

Dans ce cas, l'accélération angulaire α est constante, et en analogie avec le mouvement rectiligne uniformément varié, les équations suivantes peuvent être écrites:

• θ = θ_soit + Ω_soit T + ½ αt²
• Ω = Ω_soit + αt 
• Ω² = Ω_soit² + 2α ∙ Δθ

Exercice résolu

Premier exercice

On peut supposer que la Terre est un objet rigide qui tourne sur un axe fixe et que sa rotation est presque uniforme. Dans l'intervalle de temps Δt = 12 h, trouvez:

a) le déplacement angulaire de la terre

b) Votre vitesse angulaire

c) Accélération angulaire pendant cet intervalle de temps.

Solution à

Sachant qu'en 24 heures, la Terre prend un virage complet autour de son axe, en 12 heures, vous aurez tourné la moitié d'un tour, c'est-à-dire π radianes. S'il est considéré comme une partie de θ_initial = 0 rad, alors son déplacement angulaire est:

Peut vous servir: Principe multiplicatif: techniques de comptage et exemples

Δθ = π radians

Solution B

Comme la rotation est uniforme, la vitesse angulaire est le quotient entre le déplacement angulaire et le temps, en outre, 1 heure = 3600 s:

Ω = π rad / 12 h = π rad / (12 x 3600) s = 0.000073 RAD / S.

Solution C

L'accélération angulaire est vide, car la rotation de la terre est uniforme.

Deuxième exercice

Juan a parcouru une distance de 35 mètres sur une piste d'athlétisme circulaire dont le rayon est égal à 7 mètres. Calculez le déplacement angulaire que Juan a fait.

Solution

Étant donné que la distance de l'arche parcourue et le rayon de la circonférence est connue, la deuxième formule peut être appliquée pour connaître le déplacement angulaire fabriqué par Juan. En utilisant la formule décrite ci-dessus, vous devez θ = 35/7 = 5 radians.

Troisième exercice

Si Mario doit dans son véhicule, la moitié d'une piste de course circulaire, quel est le déplacement angulaire que Mario a fait?

Solution

Dans cet exercice, la première formule s'appliquera. Comme on sait que Mario a parcouru la moitié de la piste, on peut supposer qu'il a commencé la course à l'angle 0 ° et quand il a atteint la moitié de la circonférence, il a parcouru 180 °. Par conséquent, la réponse est de 180 ° -0 ° = 180 ° = π radians.

Quatrième exercice

Maria a une piscine circulaire. Votre chien coule dans la piscine parcourant une distance de 18 mètres. Si le rayon de la piscine est de 3 mètres, quel est le déplacement angulaire fabriqué par l'animal de compagnie de Maria?

Solution

Étant donné que la piscine est circulaire et que le rayon est connu, vous pouvez utiliser la deuxième formule.

On sait que le rayon est égal à 3 mètres, et la distance parcourue par l'animal est égale à 18 mètres. Par conséquent, le déplacement angulaire effectué est égal à θ = 18/3 = 6 radians.

Les références

1. Katz, D. 2013. Physique pour les scientifiques et les ingénieurs. Fondations et connexions. Cengage Learning.
2. Rex, un. 2011. Fondamentaux de la physique. Pearson.
3. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. Volume 1. Pearson.
4. SERAY, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7e. Élégant. Cengage Learning.
5. Tipler, P. (2006). Physique pour la science et la technologie. 5e ed. Volume 1. Éditorial Revered.