Densité de formule apparente, unités et exercices résolus

La densité apparente d'un échantillon est défini comme le quotient entre sa masse et le volume sans modification, qui comprend tous les espaces ou pores qu'il contient. S'il y a de l'air dans ces espaces, densité apparente ρ_b, soit Densité en vrac est:

ρ_b = Masse / volume = masse _particules + Masse _air /Volume _particules+ Volume _air

Figure 1. La densité apparente est très importante pour caractériser les sols. Source: Wikimedia Commons.

Lorsque la densité apparente d'un échantillon de sol est calculée, elle doit se sécher auparavant dans un four à 105 ° C jusqu'à ce que la pâte soit constante, indiquant que tout l'air s'est évaporé.

Selon cette définition, la densité apparente des sols ou Densité sèche, Il est calculé de cette manière:

ρ_s = Poids des éléments solides / volume _solides + Volume _pores

Indiquer comment m_s au poids sec ou à la masse et V_t = V_s + V_p Comme le volume total, la formule reste:

ρ_s = M_s / V_t

[TOC]

Unités

Les unités apparentes de densité dans le système international d'unités sont KG / M³. Cependant, d'autres unités telles que G / CM³ et mégagramos / mètre cube: mg / m³ Ils sont également largement utilisés.

Le concept de densité apparente est très utile en ce qui concerne les matériaux hétérogènes et poreux tels que les sols, car il indique sa capacité de drainage et d'aération, entre autres qualités.

Par exemple, les petits sols poreux ont des densités apparentes élevées, elles sont compactes et ont tendance à être facilement excitées, contrairement aux sols poreux.

Lorsqu'il y a de l'eau ou un autre liquide dans l'échantillon, le volume après séchage diminue, donc au moment des calculs, il est nécessaire de connaître la proportion d'eau d'origine (voir l'exemple résolu).

Densité du sol apparente

La densité apparente des matériaux en général, y compris le sol, est très variable, car il existe des facteurs tels que le degré de compactage, la présence de matière organique, sa texture, sa structure, la profondeur et les autres, qui affectent la forme et la quantité d'espaces poreux.

Les sols sont définis comme un mélange hétérogène de substances inorganiques, de substances organiques, d'air et d'eau. Au toucher peut être texture Fine, moyenne ou épaisse, tandis que les particules de composant peuvent être organisées de diverses manières, un paramètre appelé structure.

Les sols fins et bien structurés et avec un pourcentage élevé de matière organique ont généralement de faibles valeurs de densité apparentes. Au contraire, les sols épais, avec moins de matière organique et peu de structuration, ont tendance à avoir des valeurs plus élevées.

Peut vous servir: Test de tension: comment cela se fait, propriétés, exemples

Densité apparente selon la texture

Selon sa texture, la densité apparente a les valeurs suivantes:

Texture	Densité apparente (g / cm3)
Bien	1.00 - 1.30
Médian	1.30 - 1.cinquante
Brut	1.50 - 1.70

Ces valeurs servent de référence générale. Dans les sols turbosés, abondants dans les déchets végétaux, la densité apparente peut être aussi faible que 0.25 g / cm³, S'il s'agit d'un sol minéral volcanique, il est environ 0.85 g / cm³, Tandis que dans des sols très compactés, il atteint 1.90 g / cm³.

Densité apparente en fonction de la profondeur

La valeur de densité apparente augmente également avec la profondeur, car le sol est généralement plus compacté et a un pourcentage inférieur de matière organique.

L'intérieur de la terre est composé de couches horizontales ou de strates, appelées Horizons. Les horizons ont des textures, une composition et un compactage différentes. Par conséquent, ils présentent une variation de densité apparente.

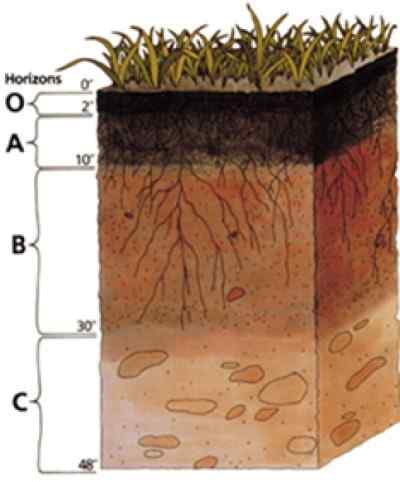Figure 2. Un profil de sol montrant les différents horizons. Source: Wikimedia Commons.

Une étude du sol est basée sur son profil, qui se compose de divers horizons qui se suivent de manière verticale.

Comment mesurer la densité apparente?

Étant donné que la variabilité de la densité apparente est très importante, il est souvent nécessaire de le mesurer directement par diverses procédures.

La méthode la plus simple consiste à extraire un échantillon du sol, en introduisant un balayage avec un cylindre métallique spatial de volume connu et en s'assurant de ne pas compacter le sol. L'échantillon extrait est scellé pour éviter la perte ou l'altération de l'humidité des caractéristiques.

Ensuite, en laboratoire, l'échantillon est extrait, pesé puis placé dans un four à 105 º C pour sécher pendant 24 heures.

Peut vous servir: corps célestes

Bien que ce soit le moyen le plus simple de trouver la densité sèche du sol, il n'est pas le plus recommandé pour les sols avec des textures très lâches ou pleines de pierres.

Pour ceux-ci, la méthode de creuser un trou est préférable et d'économiser la terre extraite, qui sera l'échantillon à sécher. Le volume de l'échantillon est déterminé en versant du sable sec ou de l'eau dans le trou cavado.

Dans tous les cas, à partir de l'échantillon, il est possible de déterminer les propriétés très intéressantes du sol pour le caractériser. L'exercice résolu suivant décrit comment le faire.

Exercice résolu

Un échantillon d'argile de 100 mm de longueur est extrait du cylindre d'échantillon, dont le diamètre interne est également de 100 mm. Avec une douleur, une masse de 1531 g est obtenue, ce qui une fois sec est réduit à 1178 g. La gravité spécifique des particules est 2.75. Il est demandé de calculer:

a) La densité apparente de l'échantillon

b) Contexte d'humidité

c) la relation vide

d) densité sèche

e) le degré de saturation

f) Contenu aérien

Solution à

Le volume sans modifier v_t C'est le volume d'origine de l'échantillon. Pour un diamètre D et le cylindre H de hauteur, le volume est:

V _cylindre = V_t = Zone de base x hauteur = πd²/ 4 = π x (100 x 10^-3 m)² x 100 x 10 ^-3 m / 4 = 0.000785 m³

La déclaration affirme que la masse de l'échantillon est m_s = 1531 g, donc selon l'équation donnée au début:

ρ_b = M_s / V_t  = 1531 g / 0.000785 m³ = 1950319 g / m³ = 1.95 mg / m³

Solution B

Comme nous avons la masse d'origine et la masse sèche, la masse de l'eau contenue dans l'échantillon est la différence de ces deux:

Peut vous servir: processus isobare: formules, équations, expériences, exercices

M _eau = 1531 g - 1178 g = 353 g

Le pourcentage d'humidité dans l'échantillon est calculé comme suit:

% Humidité = (masse _eau / Ms) x 100% = (353 g / 1178 g) = 29. 97%

Solution C

Pour trouver le rapport vide, le volume total de l'échantillon V doit être décomposé_t dans:

V _t = V _particules + Volume _pores

Le volume occupé par les particules est obtenu à partir de la masse sèche et de la gravité spécifique, données obtenues à partir de l'instruction. La gravité spécifique s_g C'est le rapport entre la densité du matériau et la densité de l'eau dans des conditions standard, donc la densité du matériau est:

ρ = s_g x ρ_eau = 2.75 x 1 g / cm³ = 2.75 g / cm³

ρ = m_s / V_s → V_s = 1.178 g / 2.75 g / cm³ = 0.428 cm³ = 0.000428 m³

Le volume des lacunes dans l'échantillon est V_V = V_t - V_s = 0.000785 m³ - 0.000428 m³ = 0.000357 m³.

La relation vide et est:

E = V_V / V_s = 0.000357 m³ / 0.000428 m³ = 0.83

Solution d

La densité sèche de l'échantillon est calculée comme indiqué dans l'introduction:

ρ_s = Poids des éléments solides / volume _solides + Volume _pores= 1178 g / 0.000785 m³ = 1.5 mg / m³

Solution E

Le degré de saturation est s = (v_eau / V_V ) X 100%. Puisque nous connaissons la masse d'eau dans l'échantillon, calculé dans l'article B) et sa densité, le calcul de son volume est immédiat:

ρ_eau = M_eau / V _eau → V_eau = 353 g / 1 g / cm³ = 353 cm³ = 0.000353 m³

D'un autre côté, le volume des lacunes a été calculé dans l'article C)

S = (0.000353 m³ / 0.000357 m³) x 100% = 98.9%

Solution F

Enfin, le pourcentage de contenu d'air est a = (V_air / V_t) X 100%. Le volume d'air correspond à:

V_V - V_eau = 0.000357 m³ - 0.000353 m³ = 0.000004 m³

A = (v_air / V_t) x 100% = (0.000004 m³/ 0.000785 m³) x100% = 0.51%

Les références

1. Berry, P. Mécanique des sols. McGraw Hill.
2. Accumulé. Densité apparente. Récupéré de: construmatique.com.
3. NRC. Densité en vrac du sol. Récupéré de: NRCS.USDA.Gouvernement.
4. Unam. Département d'édaphologie. Manuel des procédures analytiques de la physique du sol. Récupéré de: géologie.Unam.mx.
5. Wikipédia. Densité en vrac. Récupéré de: dans.Wikipédia.org.
6. Wikipédia. Sol. Récupéré de: dans.Wikipédia.org.