Combien de diamètres une circonférence a-t-elle?

Une circonférence a des diamètres infinis. Il est facile de voir qu'il en est ainsi, s'il est basé sur la définition du diamètre, qui est le segment qui passe simultanément à travers le centre de la circonférence et de deux points de celle-ci.

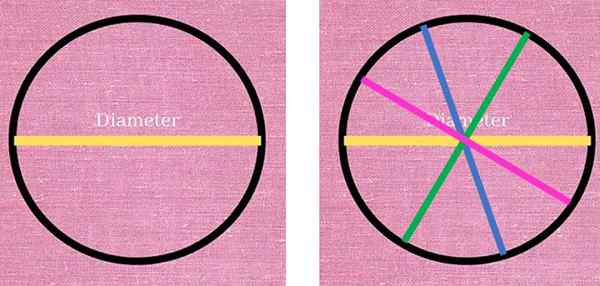
Dans la figure suivante, à gauche, la ligne jaune correspondant à un diamètre de la circonférence est observée et divisée en deux parties. Sur le côté droit, trois autres diamètres ont été dessinés en différentes couleurs: bleu, vert et rose. Tous ont la même longueur et satisfont à l'état de rejoindre deux points de la circonférence, à travers le centre de la même.

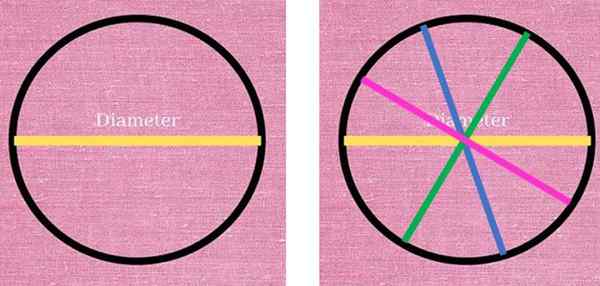Le diamètre est un segment distinctif, qui passe toujours à travers le centre de la circonférence et en joignant deux points. À gauche, le diamètre jaune divise la circonférence en deux. À droite, il y a d'autres diamètres qui divisent également la circonférence en deux moitiés. Source: F. Zapata.

Comme on peut le voir, les possibilités de dessiner des diamètres sont infinies, comme infini sont les points qui forment la circonférence. Il en va de même.

Et lors de la mise en place de deux radios opposées l'une de l'autre, un diamètre est obtenu, car le rayon en mesure la moitié.

Diamètre, radio et longueur de circonférence

Que ce soit le diamètre de toute circonférence et r, son rayon. Comme le diamètre mesure deux fois plus que la radio, il peut être écrit:

D = 2 ∙ R

Cela signifie que, si le rayon d'un cercle est, par exemple, r = 5 cm, le diamètre est d = 2 ∙ 5 cm = 10 cm.

Il peut vous servir: série Fibonacci: propriétés, relations naturelles, applications

Le diamètre est également connu sous le nom de Corde majeure. Les cordes sont des lignes ou des segments qui sont tracés entre deux points de circonférence, mais qui ne traversent pas nécessairement le centre. Seul le diamètre a cette distinction.

Dans la figure suivante, vous pouvez voir la différence et voir pourquoi, en fait, le diamètre (rouge) est la plus grande des cordes qui peut être dessinée sur la circonférence:

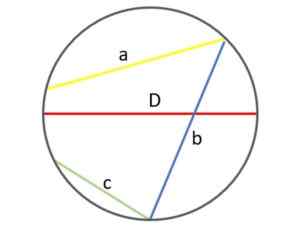Différentes cordes dans une circonférence: le diamètre est le plus grand de tous. Source: F. Zapata.

Bien sûr, la mesure du diamètre (et donc le rayon) est la même dans une circonférence donnée. En cas de variation, une circonférence plus petite ou plus grande est obtenue, selon.

D'un autre côté, la taille des chaînes de la même circonférence varie, selon la distance ou les points. Dans l'exemple montré, la corde verte «C» est ostensiblement plus courte que les cordes «A» et «B».

Et le nombre de chaînes qui peuvent être dessinées est également infinie.

Le périmètre de la circonférence

Pour sa part, la longueur de la circonférence équivaut à son périmètre ou à son contour. Il est lié à son diamètre, car plus cela est élevé, plus la circonférence est élevée (son périmètre est plus grand).

Le rapport ou le quotient entre le périmètre et le diamètre est une constante appelée π (lit "pi"). La valeur de π est 3.141592… les points suspendus indiquent que la quantité de décimales et infinie, c'est parce que Pi est un nombre irrationnel. Cependant, à des fins pratiques, Pi peut simplement rassembler 3.14

Peut vous servir: combien devez-vous ajouter à 3/4 pour obtenir 6/7?

Si le périmètre est désigné comme C et le diamètre que D, cette raison est soulevée comme suit:

C / d = π

Par conséquent, la formule pour la longueur de la circonférence est:

C = π ∙ D

Ou si préféré sur la base du rayon R:

C = 2π ∙ r

Exemple illustratif

L'image montre trois circonférences identiques, désignées par des lettres A, B et C. Dans chacun, la fourmi court la route sur les segments de couleur bleue, pour passer d'un point à une autre de la circonférence.

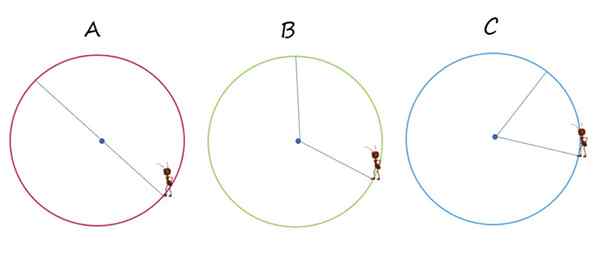La fourmi se déplace d'un point à une autre de la circonférence à travers les lignes bleues les plus minces. Source: F. Zapata.

1.- Dans lequel des cas le déplacement se produit exactement sur le diamètre de la circonférence?

Répondre

Seulement dans le cas A, parce que ce chemin passe par le centre de la circonférence et passe d'un point à un autre.

2.- Combien de radios l'insecte voyage dans chaque cas?

Répondre

Dans l'un des trois cas, la fourmi parcourt deux radios de circonférence.

3.- Lequel des chemins correspond à la plus grande distance?

Répondre

Le voyage est tout aussi long dans chaque cas, équivalent à deux radios de la circonférence.

4.- Auquel cas la fourmi est plus loin de son point de départ?

Répondre

Dans le cas A, puisque c'est au point qui est précisément devant lui, dans les autres, la fourmi est plus proche du point de départ.

5.- Et auquel cas la fourmi termine l'itinéraire plus proche de son point d'origine?

Peut vous servir: signes de regroupement

Répondre

Dans le cas C.

6.- Si le rayon des circonférences est de 20 cm, combien de centimètres est-il à chaque route?

Répondre

Étant donné que la fourmi s'étend sur une distance égale à deux radios, la distance totale parcourue est de 40 cm.

Exercices résolus

Exercice 1

Calculez le rayon d'un cercle dont le diamètre est 4.5m.

Solution

La radio est la moitié du diamètre, si cela mesure 4.5 cm, alors la radio R est 2.25 cm.

Exercice 2

Trouvez le périmètre de la circonférence de l'exercice 1.

Solution

Le périmètre est calculé par le diamètre ou par le rayon, comme préféré. Dans le premier cas:

C = π ∙ D

En supposant que π = 3.14 To Round, le remplacement des valeurs donne le résultat suivant:

C = π ∙ d = 3.14 ∙ 4.5 cm = 14.13 cm

Exercice 3

Un concepteur est invité à dessiner un logo en forme de cœur, avec les dimensions indiquées sur la figure. Les pièces incurvées correspondent à des demi-circons exacts.

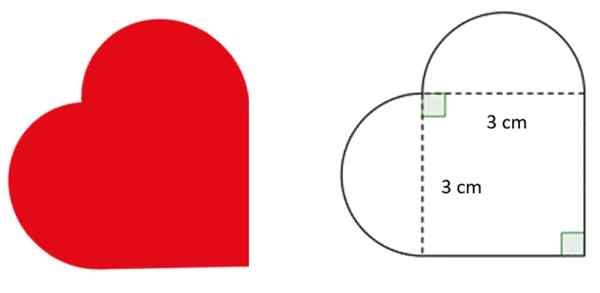
Avec cette information Réponse:

1. Quel est le rayon des semi-circonnes?
2. Combien coûte le périmètre du cœur?

Solution à

Le diamètre des semi-circuit est équivalent au côté du carré, qui est de 3 cm. Par conséquent, son rayon, qui est la moitié, mesure 1.5 cm.

Solution B

Le périmètre de la figure en forme de cœur est la somme des deux côtés externes du carré et du périmètre des semi-counes. Comme d'identité, son périmètre est égal à celui d'un cercle complet de diamètre de 3 cm:

C = π ∙ d = 3.14 ∙ 3 cm = 9.42 cm

Par conséquent, le périmètre P de la figure est:

P = 9.42 cm + 3 cm + 3 cm = 15.42 cm