Critères Triangles similaires

Quels sont les critères de similitude des triangles?

Les critères de similitude des triangles sont les règles qui permettent de savoir si deux triangles sont similaires. La similitude des figures géométriques, y compris les triangles, nécessite que les chiffres aient la même manière, bien qu'ils n'aient pas nécessairement la même taille ou la même orientation.

Pour que deux triangles soient similaires, il est nécessaire que: i) leurs côtés homologues soient proportionnels et ii) les angles internes de chacun ont la même mesure.

Figure 1. Deux triangles similaires: bien qu'ils n'aient pas la même taille, leurs côtés sont proportionnels et leurs angles internes ont une mesure égale. Source: F. Zapata.

Un rapport ou une proportion proportionnelle entre deux quantités A et B est représentée par le rapport A / B, avec B ≠ 0. Pour les triangles similaires, les proportions suivantes entre leurs côtés sont valides:

a / a '= b / b' = c / c '= r

La valeur de r est appelée Raison de similitude.

De plus, les angles internes correspondants doivent donc être de la même mesure: ∠a = ∠a '; ∠b = ∠b 'et ∠c = ∠c'. Selon ces conditions, les critères de similitude des triangles sont:

Critères 1: Deux triangles sont similaires s'ils ont deux angles internes de mesure égale. Si c'est le cas, le troisième angle mesure également le même, car la somme des angles internes dans n'importe quel triangle est de 180 °:

α = α '; β = β '

Critères 2: Les triangles sont similaires si deux côtés homologues sont proportionnels et que l'angle entre eux est le même:

a / a '= b / b'; α = α '

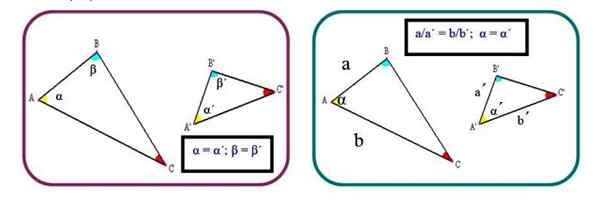Figure 2. Deux critères pour établir la similitude des triangles. Source: F. Zapata.

Critères 3: Les trois côtés homologues sont proportionnels:

a / a '= b / b' = c / c '= r

Exemples

La similitude des triangles est très utile pour calculer les hauteurs et les distances qui ne sont pas facilement mesurables directement. Grâce à quelques calculs simples, il est possible de découvrir ces longueurs en comparant des triangles similaires.

Peut vous servir: théorème fondamental de l'arithmétique: démonstration, applications, exercices

Hauteur des colonnes, des bâtiments et des arbres

On dit que le père de la géométrie dans la Grèce antique, comme Miletus (625-547 à.C.), a calculé la hauteur de la colonne d'un temple sans avoir besoin d'instruments spéciaux, en comparant simplement la longueur de l'ombre de sa canne avec celle de la colonne et en appliquant la similitude des triangles. Avec la même méthode, il a réussi à mesurer la hauteur de la grande pyramide d'Égypte et ainsi impressionner le pharaon.

La distance à la lune

Il y a une expérience simple qui est effectuée pour calculer la distance entre la Terre et la Lune. Il nécessite une monnaie, un peu de ruban adhésif et un vernier ou une règle de diplômée. Lorsque la lune est pleine, la monnaie est attachée au verre d'une fenêtre et la lune est observée d'un œil, situé de telle manière que la monnaie couvre juste la pleine lune.

Lorsque cela se produit, la raison entre le diamètre de la monnaie et la distance entre l'œil et la monnaie, est la même qu'il y a entre le diamètre de la lune et la distance entre l'œil et la lune:

Diamètre de la monnaie / distance devise = diamètre de la lune / distance à la lune

La raison en est environ 1/110. Ce qui signifie que la distance à la lune est de 110 fois le diamètre.

Actuellement, le rayon de la lune est estimé en 1737.1 km, donc son diamètre est de 3474.2 km. En remplaçant cette valeur dans la relation:

Distance de la lune = diamètre de la lune ÷ (diamètre de la devise / distance de la monnaie)

Est obtenu:

Distance de la lune = 3474.2 km ÷ (1/110) = 382.162 km

Cela peut vous servir: prisme hépagonal

Très proche de la valeur établie par 384 astronomes.000 km.

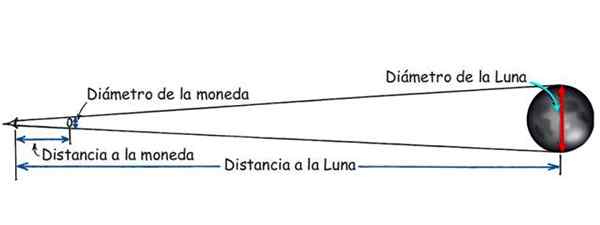figure 3. La distance à la lune peut être connue grâce à la similitude des triangles. Source: Modified Hewitt, P. Physique conceptuelle.

Distance entre un navire et le rivage

Pour mesurer la distance entre le navire et le rivage, les enjeux sont coincés sur la plage aux points A, B, C et Q. Les triangles ABC et PCQ sont similaires par les critères 1, car ils ont deux angles égaux: les deux angles ∠c = α opposés par le sommet et les deux angles droits égaux à 90º: ∠b = ∠q.

On dit que deux triangles situés de cette manière Position des thales Et ils sont toujours similaires. Les triangles sont identifiés dans la position de Thales pour avoir un angle commun et les côtés opposés à cet angle sont parallèles.

Dans la section suivante, il y a un exercice avec des valeurs numériques.

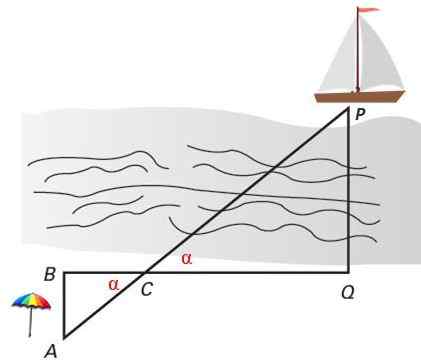Figure 4. Deux triangles similaires en position Thales servent à calculer la distance perpendiculaire d'un navire au rivage. Source: F. Zapata.

Exercices résolus

Exercice 1

Vous voulez savoir jusqu'où le voilier est ancré dans la figure précédente, à partir d'un point situé sur le rivage de la plage, pour lesquels les enjeux sont cloués aux points A, B, C et Q, déterminant ainsi le triangle ABC, qui est similaire à PCQ, mais dont les côtés sont plus faciles à mesurer.

Calculez la distance perpendiculaire PQ entre le navire et le rivage, par la similitude des triangles, si les distances disponibles sont:

Ab = 12 m

BC = 16 m

Qc = 60 m

Solution

Les proportions entre les côtés homologues sont:

Ab / qp = bc / cq = 16 m / 60 m = 0.267

Par conséquent 0.267 est la raison de la similitude:

Ab / qp = 0.267

Qp = ab / 0.267 = 12 m / 0.267 = 44.9 m

Exercice 2

Dans le triangle suivant: combien mesure le segment d'annonce?

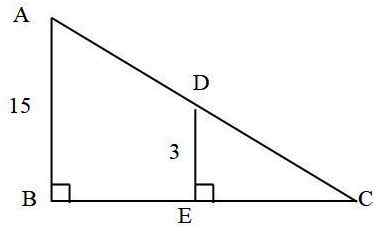
On sait que:

• AC = 25 cm
• Ab = 15 cm
• DE = 3 cm

Peut vous servir: Multiples de 2: quelles sont et explications

Solution

Les triangles sont similaires, car ils partagent un angle qui est ∠c et les côtés de et AB sont parallèles. Le rapport de similitude est calculé par:

R = ab / de = 15 cm / 3 cm = 5

Et aussi à travers:

R = AC / DC

Donc dc = ac / r = 25 cm / 5 = 5 cm

Puisque:

AC = AD + DC

Il s'ensuit que AD = AC - DC = 25 cm - 5 cm = 20 cm

Exercice 3

Un triangle isocèle a un périmètre de 49 cm et une base de 21 cm. Calculez le périmètre d'un triangle similaire à celui-ci, mais dont la base mesure 4 cm.

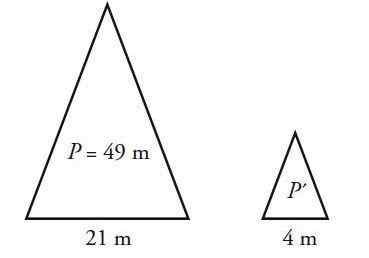
Solution

Le triangle isocèle a deux côtés égaux, différents de la base b. Soit ℓ la mesure des côtés et du périmètre, qui se compose de la somme des trois côtés. Pour le plus grand triangle:

P = 2 ℓ + b = 49 cm

2 ℓ + 21 cm = 49 cm → ℓ = (49-21) cm / 2 = 14 cm

Maintenant, la proportion entre les côtés des triangles est augmentée, celles du petit triangle sont symbolisées par des primes:

B / b '= ℓ / ℓ'

21 cm / 4cm = 14 cm / ℓ '→ ℓ' = 14 cm / (21 cm / 4cm) = 2.67 cm

Le périmètre du petit triangle sera:

P '= 2 ℓ' + b '= (2 x 2.67) cm + 4 cm = 9.33 cm.

Les références

1. Alexander, D. 2013. Géométrie. 5e. Édition. Cengage Learning.
2. Hewitt, Paul. 2012. Sciences physiques conceptuelles. 5e. Élégant. Pearson.
3. Clemens, s. Géométrie avec applications. Addison Wesley.
4. Ibáñez, p. 2010. Mathématiques III. Cengage Learning.
5. Jiménez, R. Mathématiques II: géométrie et trigonométrie. 2e. Édition. Pearson.
6. Stewart, J. 2007. Précalation. 5e. Édition. Cengage Learning.
7. Vicmat. Samos Aristarco: Mesures du système solaire. Récupéré de: vicmat.com