Intégration Signification constante, calcul et exemples

La Constante d'intégration C'est une valeur ajoutée au calcul des antidérivatifs ou des intégrales, il sert à représenter les solutions qui composent la primitive d'une fonction. Exprime une ambiguïté inhérente où une fonction a un nombre infini de primitif.

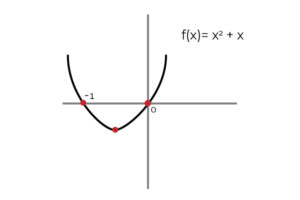
Par exemple, si la fonction est prise: f (x) = 2x + 1 et que nous obtenons son antidérivatif:

∫ (2x + 1) dx = x² + X + C ; Où C C'est le Constante d'intégration et représente graphiquement la traduction verticale entre les possibilités infinies de primitive. Il est correct de dire que (x² + x) c'est ongle du F primitif (x).

Source: auteur

De la même manière que vous pouvez définir (x² + X + C ) comme la primitive de f (x).

[TOC]

Propriété inverse

On peut noter que lorsqu'il a dérivé l'expression (x² + x) La fonction f (x) = 2x + 1 est obtenue. Cela est dû à la propriété inverse entre la dérivation et l'intégration des fonctions. Cette propriété permet d'obtenir des formules d'intégration à partir de la différenciation. Qui permet la vérification des intégrales à travers les mêmes dérivés.

Source: auteur

Cependant (x² + x) Ce n'est pas la seule fonction dont la dérivée est égale à (2x + 1).

1. D (X² + x) / dx = 2x + 1
2. D (X² + x + 1) / dx = 2x + 1
3. D (X² + x + 2) / dx = 2x + 1
4. D (X² + x + 3) / dx = 2x + 1
5. D (X² + X + C) / dx = 2x + 1

Où 1, 2, 3 et 4 représentent une primitive particulière de f (x) = 2x + 1. Tandis que 5 représente l'intégrale indéfinie ou primitive de f (x) = 2x + 1.

Source: auteur

La primitive d'une fonction est obtenue par l'antidérivation ou le processus intégral. Où f sera un F primitif si les éléments suivants sont remplis

• y = ∫ f (x) dx = F (x) + c; C = Constante d'intégration
• F '(x) = f (x)

Il est apprécié qu'une fonction a une seule dérivée, contrairement à sa primitive infinie résultant de l'intégration.

L'intégrale indéfinie

 ∫ f (x) dx = f (x) + c

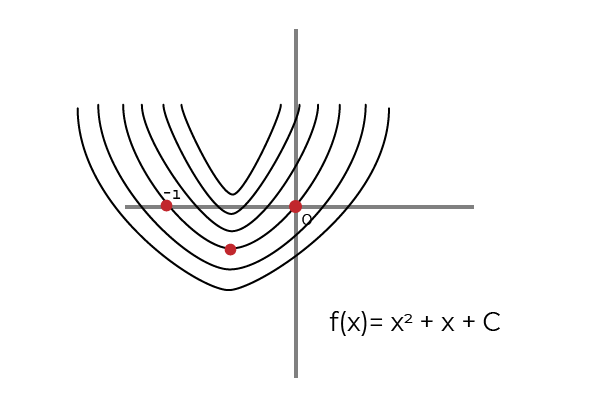
Il correspond à une famille de courbes avec le même schéma, qui éprouvent une incongruité dans la valeur des images de chaque point (x, y). Chaque fonction qui remplit ce modèle sera une primitive individuelle et l'ensemble de toutes les fonctions est connue sous le nom Intégral indéfini.

La valeur du Constante d'intégration Ce sera celui qui différencie chaque fonction dans la pratique.

La Constante d'intégration Il suggère un déplacement vertical dans tous les graphiques qui représentent le primitif d'une fonction. Où le parallélisme est observé entre eux, et le fait que C C'est la valeur du déplacement.

Selon les pratiques communes Constante d'intégration Il est indiqué avec la lettre «C» après un ajout, bien qu'en pratique il soit indifférent si la constante ajoute ou soustrait. Sa valeur réelle peut être trouvée de différentes manières en fonction de différents conditions initiales.

Autres significations de la constante d'intégration

On a déjà parlé de la façon dont Constante d'intégration est appliqué dans la branche de calcul intégral; Représentant une famille de courbes qui définissent l'intégrale indéfinie. Mais de nombreuses autres sciences et branches ont attribué des valeurs très intéressantes et pratiques Constante d'intégration, qui ont facilité le développement de plusieurs études.

Peut vous servir: rectangle trapézoïde: propriétés, relations et formules, exemples

Dans la physique La constante d'intégration peut prendre plusieurs valeurs en fonction de la nature des données. Un exemple très courant est de connaître la fonction V (t) qui représente le vitesse d'une particule par rapport au temps t. On sait que lors du calcul d'un V primitif (t), la fonction est obtenue R (t) qui représente le position de la particule par rapport au temps.

La Constante d'intégration représentera la valeur de la position initiale, c'est-à-dire pour le moment t = 0.

De même, si la fonction est connue À)  qui représente le accélération de la particule par rapport au temps. La primitive de a (t) entraînera la fonction V (t), où le Constante d'intégration Ce sera la valeur de la vitesse initiale v₀.

Dans la économie, en obtenant la primitive d'une fonction de coût par intégration. La Constante d'intégration représentera les coûts fixes. Et tant d'autres applications qui méritent un calcul différentiel et intégral.

Comment la constante d'intégration est-elle calculée?

Pour le calcul du Constante d'intégration, Il sera toujours nécessaire de connaître le conditions initiales. Qui sont responsables de définir lequel des primitifs possibles est le correspondant.

Dans de nombreuses applications, il est traité comme une variable indépendante en temps (t), où la constante C Prenez les valeurs qui définissent le conditions initiales du cas particulier.

Si l'exemple initial est pris: ∫ (2x + 1) dx = x² + X + C

Une condition initiale valide peut être pour conditionner le graphique pour passer à travers une coordonnée spécifique. Par exemple, il est connu que primitif (x² + X + C) Passer par le point (1, 2)

F (x) = x² + X + C; C'est la solution générale

F (1) = 2

Nous remplaçons la solution générale dans cette égalité

F (1) = (1)² + (1) + c = 2

Où il est facilement déduit que C = 0

De cette façon, la primitive correspondante pour ce cas est F (x) = x² + X

Il existe différents types d'exercices numériques qui fonctionnent avec Constantes d'intégration. En fait, le calcul différentiel et intégral ne cesse pas d'être appliqué dans les enquêtes actuelles. À différents niveaux académiques, vous pouvez trouver; Du calcul initial, à travers la physique, la chimie, la biologie, l'économie, entre autres.

Il est également apprécié dans l'étude de équations différentielles, où le Constante d'intégration Vous pouvez prendre diverses valeurs et solutions, celle-ci en raison des références multiples et intégrations qui sont effectuées dans cette affaire.

Exemples

Exemple 1

1. Un canon situé à 30 mètres de haut tire verticalement un projectile. Il est connu que la vitesse initiale du projectile est de 25 m / s. Déterminer:

• La fonction qui définit la position du projectile par rapport au temps.
• L'heure de vol ou l'heure dans laquelle la particule joue le sol.

Il peut vous servir: les 8 types d'erreurs de mesure (avec des exemples)

Il est connu que dans une accélération de mouvement rectiligne uniformément variée est une valeur constante. C'est le cas du lancement de projectile, où l'accélération sera la gravité

G = - 10 m / s²

Il est également connu que l'accélération est la seconde dérivée de la position, indiquant une double intégration dans la résolution de l'exercice, obtenant ainsi deux Constantes d'intégration.

A (t) = -10

V (t) = ∫a (t) dt = ∫ (-10t) dt = -10t + C₁

Les conditions initiales de l'exercice indiquent que la vitesse initiale est V₀ = 25 m / s. C'est la vitesse au moment de l'heure t = 0. De cette façon, il est réalisé que:

V (0) = 25 = -10 (0) + C₁   et C₁ = 25

La fonction de vitesse en cours de définition

V (t) = -10t + 25; Vous pouvez voir la similitude avec la formule MRUV (V_F = V₀ + A x t)

En homologue, la fonction de vitesse est intégrée pour réaliser l'expression qui définit la position:

R (t) = ∫v (t) dt = ∫ (-10t + 25) dt = -5t² + 25t + C₂

R (t) = -5t² + 25t + C₂  (Position primitive)

La position initiale r (0) = 30 m est connue. Alors la primitive particulière du projectile est calculée.

R (0) = 30m = -5 (0)² + 25 (0) + C₂ . Où C₂ = 30

La première section est résolue depuis R (t) = -5t² + 25T + 30  ; Cette expression est homologue de la formule de déplacement dans Mruv R (t) = R₀ + V₀T - gt²/ 2

Pour la deuxième section, l'équation quadratique doit être résolue: -5T² + 25T + 30 = 0

Puisqu'il conditionne la particule pour atteindre le sol (position = 0)

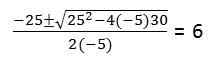Source: auteur

En fait, l'équation de 2e année lance 2 solutions T: 6, -1. La valeur t = -1 est ignorée car ce sont des unités de temps dont le domaine n'inclut pas les nombres négatifs.

De cette façon, la deuxième section où le temps de vol est égal à 6 secondes est résolu.

Exemple 2

2. Trouvez le F (x) primitif qui remplit les conditions initiales:

• f "(x) = 4; f '(2) = 2; f (0) = 7

Avec les informations du deuxième dérivé f "(x) = 4, le processus antidérivation commence

f '(x) = ∫f "(x) dx

∫4 dx = 4x + c₁

Ensuite, la connaissance de la condition f '(2) = 2 procède:

4 (2) + c₁ = 2

C₁ = -6 et f '(x) = 4x - 8

Continuez de la même manière pour la seconde Constante d'intégration

f (x) = ∫f '(x) dx
∫ (4x - 8) dx = 2x² - 8x + c₂

La condition initiale f (0) = 7 est connue et continue:

2 (0)² - 8 (0) + C₂ = 7

C₂ = 7 et f (x) = 2x² - 8x + 7

• f "(x) = x² ; f '(0) = 6; f (0) = 3

Semblable au problème précédent, nous définissons les premiers dérivés et la fonction d'origine des conditions initiales.

f '(x) = ∫f "(x) dx

∫ (x²) Dx = (x³/ 3) + c₁

Avec l'état f '(0) = 6 procède:

Peut vous servir: Théorie des ensembles: caractéristiques, éléments, exemples, exercices

(0³/ 3) + c₁ = 6; Où₁ = 6 et f '(x) = (x³/ 3) + 6

Puis le second Constante d'intégration

f (x) = ∫f '(x) dx

∫ [(x³/ 3) + 6] dx = (x⁴/ 12) + 6x + c₂

La condition initiale f (0) = 3 est connue et continue:

[(0)⁴/ 12] + 6 (0) + C₂ = 3; Où₂ = 3

La primitive particulière est obtenue

f (x) = (X⁴/ 12) + 6x + 3

Exemple 3

3. Définissez les fonctions primitives compte tenu des dérivés et un point du graphique:

• dy / dx = 2x - 2 qui passe par le point (3, 2)

Il est important de se rappeler que les dérivés se réfèrent à la pente de la ligne tangente à la courbe à un certain point. Où il n'est pas correct de supposer que le graphique du dérivé touche le point indiqué, car il appartient au graphique de la fonction primitive.

De cette façon, nous exprimons l'équation différentielle comme suit:

dy = (2x - 2) dx  ; Ensuite, lorsque vous appliquez les critères antidérivation, vous avez:

∫dy = ∫ (2x - 2) dx

y = x² - 2x + c

Application de l'état initial:

2 = (3)² - 2 (3) + c

C = -1

Est obtenu: f (x) = x² - 2x - 1

• dy / dx = 3x² - 1 qui passe par le point (0, 2)

Nous exprimons l'équation différentielle comme suit:

dy = (3x² - 1) dx  ; Ensuite, lorsque vous appliquez les critères antidérivation, vous avez:

 ∫dy = ∫ (3x² - 1) dx

y = x³ - x + c

Application de l'état initial:

2 = (0)² - 2 (0) + c

C = 2

Est obtenu: f (x) = x³ - x + 2

Exercices proposés

Exercice 1

1. Trouvez le F (x) primitif qui remplit les conditions initiales:

• f "(x) = x; f '(3) = 1; f (2) = 5
• f "(x) = x + 1; f '(2) = 2; f (0) = 1
• f "(x) = 1; f '(2) = 3; f (1) = 10
• f "(x) = -x; f '(5) = 1; f (1) = -8

Exercice 2

2. Un ballon qui monte avec 16 pieds / s de vitesse libère une veste de sable d'une hauteur de 64 pieds au-dessus du niveau du sol.

• Définir l'heure de vol
• Quel sera le vecteur V_F Lorsque vous touchez le sol?

Exercice 3

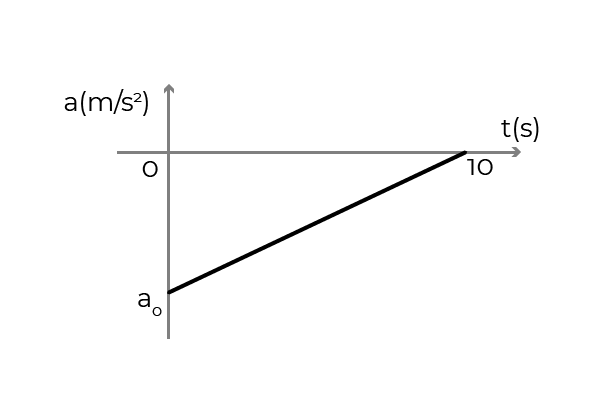
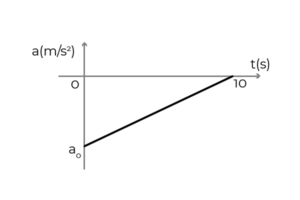
3. La figure montre le graphique d'accélération - le temps d'une voiture qui se déplace au sens positif de l'axe x. La voiture se rendait à une vitesse constante de 54 km / h lorsque le conducteur a appliqué les freins pour s'arrêter en 10 secondes. Déterminer:

• L'accélération initiale de la voiture
• La vitesse de la voiture à t = 5s
• Le déplacement de la voiture pendant le freinage

Source: auteur

Exercice 4

4. Définissez les fonctions primitives compte tenu des dérivés et un point du graphique:

• dy / dx = x qui passe par le point (-1, 4)
• dy / dx = -x² + 1 qui passe par le point (0, 0)
• dy / dx = -x + 1 qui passe par le point (-2, 2)

Les références

1. Calcul intégral. Méthodes intégrales et d'intégration indéfinies. Wilson, Velásquez Bastidas. Université Magdalena 2014
2. Stewart, J. (2001). Calcul d'une variable. Précoce. Mexique: Thomson Learning.
3. Jiménez, R. (2011). Mathématiques VI. Calcul intégral. Mexique: Pearson Education.
4. Physique je. Mc Graw Hill