Conservation du principe linéaire de Simia, exemples, exercices.

La Conservation de l'élan linéaire d'un corps établit que le produit de sa masse par son vecteur de vitesse est une quantité constante, lorsque le corps est exempt d'interaction avec d'autres corps et avec la vitesse mesurée par rapport à un système de référence fixe ou non aigu.

Lorsqu'il y a plusieurs corps qui interagissent uniquement entre eux, mais pas avec l'environnement extérieur, alors le élan linéaire de l'ensemble reste également constant dans le temps.

Un astronaute dans l'espace est exempt de toute interaction, donc son moment linéaire

Le moment linéaire, la quantité de mouvement linéaire ou simplement le élan, Il est indiqué avec la lettre p Et c'est un montant vectoriel:

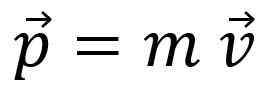
Le moment linéaire n'est pas le même que la vitesse, bien que le rapport soit évident: par exemple, un camion qui passe à 20 km / h a plus de temps linéaire qu'un vélo qui se déplace à la même vitesse.

Pour que le moment linéaire d'un corps change, il est nécessaire qu'une force externe nette agisse dessus, sinon il reste constant. De plus, le moment linéaire P d'un système formé par Norme n C'est la somme vectorielle des moments individuels:

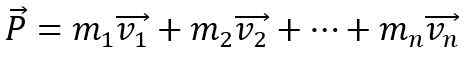
[TOC]

Principe de conservation de la quantité de mouvement linéaire

Dans un corps sans forces (ou celui dans lequel toutes les forces dessus sont annulées), il arrive que le moment linéaire.

De la même manière, il passe dans un système formé par plusieurs corps qui n'interagissent que les uns avec les autres, mais pas avec l'environnement extérieur: le moment linéaire total du système reste fixe pendant l'évolution de l'ensemble de l'ensemble.

Ce principe de conservation est énoncé comme ceci:

Le moment linéaire total d'un ensemble de normes N qui interagit uniquement les uns avec les autres, mais pas avec l'environnement extérieur, est une quantité invariable dans le temps.

Et mathématiquement, il est exprimé comme suit:

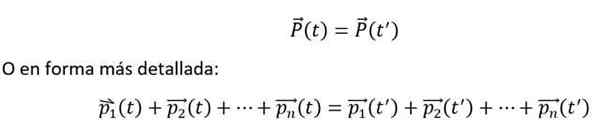
L'égalité précédente est remplie, si et seulement si le n-Les corps interagissent les uns avec les autres, mais pas avec l'environnement extérieur. De plus, les moments individuels doivent toujours être mesurés par rapport à un système de référence inertielle.

Exemples

Exemple 1

Deux astronautes dans l'espace sont retirés des mains et restent en position fixe par rapport au navire. Mais ils se poussent, ils commencent à se séparer dans des directions opposées, quand ils sont vus du navire.

Il peut vous servir: Théorie du Big Bang: caractéristiques, étapes, preuves, problèmes

Dans ce cas, comme l'interaction entre les astronautes n'est parmi eux que par la force de contact de leurs mains, le moment linéaire total. C'est-à-dire le temps linéaire total 0.

Cependant, le moment linéaire de chaque astronaute a changé. Initialement, chacun a eu un moment linéaire 0 par rapport au navire, mais après avoir poussé, l'un sort dans une direction et l'autre dans la direction opposée, avec des moments linéaires non nuls de magnitude égale et d'adresses contraires.

Ainsi, lorsque les moments individuels sont ajoutés vectoriellement, l'élan linéaire total initial est obtenu en conséquence, ce qui est vide.

D'un autre côté, la conservation du moment linéaire. Mais le résultat de la multiplication de sa masse par sa vitesse est égal au produit obtenu en multipliant la masse de l'autre par la vitesse de l'autre.

Exemple 2

Un chiot est sur une plate-forme flottante dans un lac d'eaux calmes et son propriétaire le voit à partir d'un quai. Au début, la plate-forme et le chiot sont au repos, mais lorsque le chiot veut approcher le propriétaire, la plate-forme s'éloigne du quai.

L'explication de cette observation est précisément dans le principe de conservation du montant linéaire. Le système se compose du chiot et de la plate-forme.

Le chiot peut marcher sur la plate-forme grâce à la force de frottement entre ses jambes et la surface, dans ce cas, la force de frottement est une force interne d'interaction entre elle et la plate-forme.

L'ensemble est un système isolé, et la plate-forme peut se déplacer horizontalement sur le lac, sans toute résistance à mouvement. D'un autre côté, dans la direction verticale, toutes les forces sont l'équilibre et compensées, et l'ensemble n'a pas de mouvement dans cette direction.

Par conséquent, dans cette situation, toutes les hypothèses sont respectées afin que le principe de conservation de l'élan linéaire soit appliqué.

Exemple 3

Un Esquimau est pris au centre d'une glace, la glace est si lisse que peu importe l'essai, l'Eskimo se glisse et reste toujours au même endroit.

La seule façon possible que l'Esquimat quitte le lac, c'est qu'il se trouve dans la direction contraire à laquelle un objet lourd qui porte dans son sac à dos (en supposant un).

Peut vous servir: optique géométrique: quelles études, lois, applications, exercices

Applications

Expédier dans l'espace

La conservation du moment linéaire. Dans ce cas, l'impulsion du navire est obtenue par expulsion de gaz à grande vitesse, afin que la fusée puisse se déplacer dans la direction opposée dans laquelle ils ont été expulsés.

Si le navire est à l'origine au repos, lorsque le carburant est brûlé et expulsé, la force d'expulsion se produit contre le navire lui-même. C'est une force interne entre les gaz et le navire. Il n'y a pas de forces extérieures et applique donc la conservation du moment linéaire.

Comme le moment linéaire des gaz est le même et contraire à celui du navire, il parvient à quitter le repos, et en continuant à expulser les gaz, augmente sa quantité de mouvement et donc sa vitesse.

Vie quotidienne

Un autre cas pour la conservation du moment linéaire.

On pourrait faire valoir que dans ce cas, le principe ne s'applique pas, car il existe une force externe: la résistance offerte par le bois au clou de girofle.

Cependant, au moment du contact, la force que le marteau imprime vers l'ongle est une force interne (entre le système qui est l'ongle et le marteau) beaucoup plus grand que la résistance que le bois s'oppose, et donc ce dernier est négligeable.

Le moment linéaire entier du marteau, qui est assez grand en raison de sa grande masse et de sa vitesse, est transféré à l'ongle juste après la collision. Notez que tout le moment est transféré, mais pas toute l'énergie cinétique du marteau, car une partie de celle-ci est transformée en énergie thermique en l'ongle et le marteau, qui augmente sa température après l'impact.

Exercices

Exercice 1

Les astronautes d'Andrew et de Berenice sont sortis de la station spatiale prise des deux mains et au repos par rapport à la station. Ils conduisent poussent leurs mains contre ceux de l'autre et ils sont libérés. Si Andrew, 70 kg de masse se déplace à 1 m / s par rapport à la station, quelle est la vitesse de Bérénice avec 49 kg de masse?

Solution

Dans ce cas, l'hypothèse de la conservation de l'élan linéaire est clairement appliquée, car il n'y a pas de forces externes dans l'espace extérieur. La force avec laquelle leurs mains poussent les deux astronautes est une force interne.

Il peut vous servir: diffraction des vagues: concept et exemples

Supposons que la masse d'Andrew est m_pour Et celui de Berenice m_b. De même, les vitesses des deux après l'impulsion sont V_pour Pour Andrew et V_b Pour Berenice. Ensuite, la conservation de l'élan linéaire est appliquée comme suit:

M_pour∙0 + M_b∙0 = M_pour∙V_pour+ M_b∙V_b

Effacer la vitesse de Berenice que vous avez:

V_b = - (m_pour / M_b) ∙ V_pour

Placer des valeurs numériques:

V_b = - (70/49) ∙ (1m / s) ou = -1,43m / s ou

C'est-à-dire que Bérénice se déplace rapidement de 1,43 m / s dans la direction opposée d'Andrew.

Exercice 2

Un chiot se dirige vers son propriétaire au-dessus d'une plate-forme semi-siffée. Source: F. Zapata.

Une pâte de 5 kg est au repos sur une plate-forme de 15 kg qui flotte, également au repos, sur un lac immobile. Si le chiot commence à marcher sur la plate-forme à un rythme de 0,5 m / s par rapport à cela. À quelle vitesse le chiot et la plate-forme concernant un observateur fixe à la terre?

Solution

Il sera considéré comme un système de référence inertielle au quai où est le propriétaire du chiot. Initialement, le chiot et la plate-forme flottante sont au repos par rapport au quai.

Lorsque le chiot décide de se diriger vers le propriétaire rapidement V ' En ce qui concerne la plate-forme, la plate-forme s'éloigne du ressort avec une vitesse +V. La vitesse du chiot par rapport au quai est obtenue par la somme vectorielle de sa vitesse par rapport à la plate-forme plus la vitesse de la plate-forme et le désigne par:

V = -V' + V

Comme la résistance de l'eau au mouvement de la plate-forme est pratiquement nulle en raison de sa basse vitesse, il peut être affirmé que le système composé de Le chiot + la plate-forme Il s'agit d'un système isolé et le principe de conservation de l'élan linéaire est appliqué:

0 = M ∙ V + M ∙ V

Rappelant que V = V '+ V vous avez:

0 = -M ∙ V '+ M ∙ V + M ∙ V

C'est-à-dire: m ∙ v '= (m + m) ∙ v

Donc v = [m / (m + m)] v 'y v = - (m / m) v = - [m / (m + m)] v'

Le remplacement des valeurs numériques est:

V = [5 / (5 +15)] ∙ 0,5 m / s = 0,125 m / s

C'est la vitesse à laquelle la plate-forme à ressort s'éloigne.

V = - (15/20) ∙ 0,5 m / s = -0,375 m / s

Et c'est la vitesse à laquelle le chiot s'approche du quai.

Les références

1. université de Duke. Systèmes de particules. Récupéré de: webhome.Phy.Duc.Édu.
2. Rex, un. 2011. Fondamentaux de la physique. Pearson.
3. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. Volume 1. Pearson.
4. SERAY, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7e. Élégant. Cengage Learning.
5. Tipler, P. (2006). Physique pour la science et la technologie. 5e ed. Volume 1. Éditorial Revered.