Étapes de cycle de carnot, applications, exemples, exercices

Il Cycle de carnot C'est la séquence de processus thermodynamiques qui se déroulent dans un moteur Carnot, un dispositif idéal qui ne se compose que de processus réversibles; c'est-à-dire ceux qui, ayant eu lieu, peuvent revenir à l'état initial.

Ce type de moteur est considéré comme idéal, car il n'a pas la dissipation, la friction ou la viscosité qui se produisent dans les machines réelles, transformant l'énergie thermique en travail utilisable, bien que la conversion ne soit pas effectuée à 100%.

Figure 1. Une locomotive à vapeur. Source: Pixabay

Un moteur est construit sur la base d'une substance capable de faire du travail, comme le gaz, l'essence ou la vapeur. Cette substance est soumise à divers changements de température et éprouve à son tour des variations de sa pression et de son volume. De cette façon, il est possible de déplacer un piston à l'intérieur d'un cylindre.

[TOC]

Quel est le cycle carnot?

Le cycle carnot se déroule dans un système appelé carnot ou c moteur, qui est un gaz idéal verrouillé dans un cylindre et fourni avec un piston, qui est en contact avec deux sources à différentes températures t₁ et T₂ comme celui illustré dans la figure suivante à gauche.

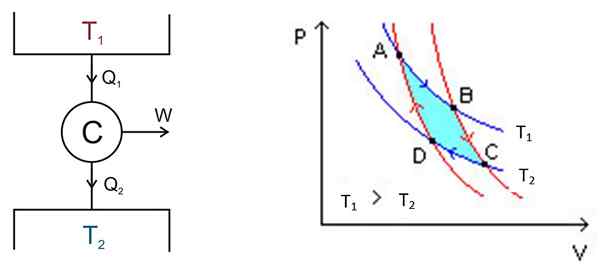Figure 2. À gauche un schéma de la machine C arnot, à droite le diagramme PV. Source de la figure de gauche: Keta - propre travail, CC par 2.5, https: // communes.Wikimedia.org / w / index.Php?Curid = 681753, figure droite Wikimedia Commons.

Il existe les processus suivants dans un mode difficile:

1. Une certaine quantité de chaleur est fournie à l'appareil_entrée = Q₁ À partir du réservoir thermique à haute température t₁.
2. Le moteur Carnot C effectue un travail w grâce à cette chaleur fournie.
3. Une partie de la chaleur utilisée: les déchets q_sortie, Il est transféré dans le réservoir thermique qui est à une température plus basse t₂.

Étapes de cycle carnot

L'analyse est effectuée par un diagramme P -V (volume de pression), comme le montre la figure 2 (figure de droite). L'objectif du moteur peut être de garder le dépôt thermique 2 froid, en extraction de la chaleur. Dans ce cas, c'est un Machine à réfrigérant. Si au contraire, vous souhaitez donner de la chaleur au dépôt thermique 1, alors c'est un bombe de chaleur.

Le diagramme P -V montre les changements de pression - Température du moteur dans deux conditions:

- Maintenir la température constante (processus isotherme).

- Pas de transfert de chaleur (isolation thermique).

Les deux processus isothermes doivent être connectés, ce qui est réalisé au moyen d'une isolation thermique.

Point de départ

Vous pouvez commencer à n'importe quel point du cycle, dans lequel le gaz a certaines pression, volume et conditions de température. Le gaz subit une série de processus et peut revenir aux conditions de départ pour commencer un autre cycle, et toujours l'énergie interne finale est la même que la première. Puisque l'énergie est préservée:

Travail effectué par C = Heat d'entrée - chaleur de départ

Δw = q_entrée - Q_sortie

La zone incluse dans ce cycle ou boucle, en turquoise sur la figure, équivaut précisément au travail effectué par le moteur Carnot.

Les points A, B, C et D sont marqués dans la figure 2. Il commencera par le point de suivre la flèche bleue.

Première étape: extension isotherme

La température entre les points A et B est t₁. Le système absorbe la chaleur du dépôt thermique 1 et souffre d'une expansion isotherme. Puis le volume augmente et la pression diminue.

Cependant, la température reste en t₁, Depuis quand le gaz se dilate, il refroidit. Par conséquent, son énergie interne reste constante.

Il peut vous servir: Graff Van Generator: Parties, comment cela fonctionne, applications

Deuxième étape: Expansion adiabatique

Au point B, le système commence une nouvelle extension dans laquelle le système ne gagne pas ou ne perd pas de chaleur. Ceci est réalisé en le mettant en isolation calorique comme indiqué précédemment. C'est donc une expansion adiabatique qui continue de pointer C après la flèche rouge. Le volume augmente et la pression diminue jusqu'à ce qu'elle atteigne sa valeur la plus basse.

Troisième étape: compression isotherme

Commencez au point C et se terminez par D. L'isolation est supprimée et le système entre en contact avec le dépôt thermique 2, dont la température t₂ C'est moins. Le système donne de la chaleur des déchets dans le réservoir thermique, la pression commence à augmenter et le volume pour diminuer.

Quatrième étape: compression adiabatique

Atteint au point D, le système remonte à l'isolation thermique, la pression augmente et le volume diminue jusqu'à atteindre les conditions d'origine du point A. Ensuite, le cycle est à nouveau répété.

Théorème de Carnot

Le théorème de Carnot a été postulé pour la première fois au début du 19e siècle par le physicien français Sadi Carnot. En 1824, Carnot, qui faisait partie de l'armée française, a publié un livre dans lequel il a proposé la réponse à la question suivante: Dans quelles conditions une machine thermique a une efficacité maximale? Carnot a ensuite établi ce qui suit:

Aucun moteur thermique fonctionnant entre deux dépôts thermiques n'est plus efficace que le moteur Carnot.

Le rendement η d'un moteur thermique est donné par le rapport entre le travail effectué w et la chaleur absorbée Q:

Performance = travail effectué / chaleur absorbée

De cette façon, les performances de tout moteur thermique I sont: η = w / q. Alors que les performances d'un moteur carnot r sont η '= w / q', dans le cas des deux moteurs, ils sont capables d'effectuer le même travail.

Le théorème de Carnot déclare que η n'est jamais supérieur à η '. Sinon, il tombe en contradiction avec la deuxième loi de la thermodynamique, selon lequel un processus dans lequel le résultat est que la chaleur d'un corps de température plus basse est impossible à atteindre une autre de température plus élevée sans recevoir une aide externe. Donc:

η _< η^'

Démonstration du théorème de Carnot

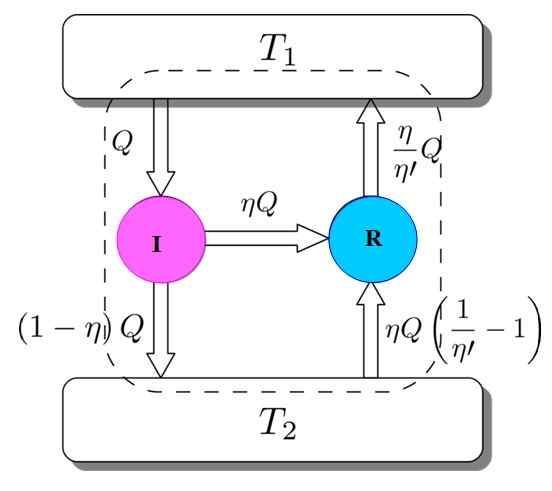
Pour montrer que c'est ainsi, considérons le moteur Carnot agir comme une machine de réfrigérateur entraînée par un moteur I. Cela est possible puisque le moteur Carnot fonctionne par des processus réversibles, comme spécifié au début.

figure 3. Démonstration du théorème de Carnot. Source: Netheril96 [CC BY-SA 3.0 (https: // CreativeCommons.Org / licences / by-sa / 3.0)]

Vous avez les deux: I et R travaillant avec les mêmes dépôts thermiques et il sera supposé que η _> η^'. Si en cours de route, une contradiction est atteinte avec la deuxième loi de la thermodynamique, le théorème de Carnot est démontré par réduction de l'absurdité.

La figure 3 aide à suivre le processus. Le moteur I prend une quantité de chaleur Q, qui se divise de cette manière: faire du travail sur R équivalent à w = ηq et le reste est la chaleur transférée (1 -η) Q au réservoir thermique t₂.

Étant donné que l'énergie est préservée, tout est accompli:

ET_entrée = Q = travailler w + chaleur affectée à t₂ = ηq + (1 -η) q = e_sortie

Maintenant, la machine à réfrigérateur Carnot R prend le réservoir thermique 2 une quantité de chaleur donnée par:

Il peut vous servir: Imantation: ce qui consiste, la méthode et les exemples

(η / η ') (1 -η') q =

L'énergie doit également être conservée dans ce cas:

ET_entrée = ηq + (η / η ') (1 -η') q = (η / η ') q = q' = e_sortie

Le résultat est le transfert vers le réservoir thermique t₂ d'une quantité de chaleur donnée par (η / η ') q = q'.

Si η est supérieur à η ', cela signifie que le gisement thermique la plus haute température est arrivé plus de chaleur que je ne l'ai pris à l'origine. Étant donné qu'aucun agent externe, comme une autre source thermique, n'a participé, la seule façon de se produire est que le dépôt thermique le plus froid donne la chaleur.

Cela n'est pas d'accord avec la deuxième loi de la thermodynamique. Il est alors conclu qu'il n'est pas possible que η^' Être inférieur à η, donc le moteur I ne peut pas avoir plus de performances que la machine Carnot R.

Théorème corollaire et limitations

Le corollaire du théorème Carnot indique que deux machines carnot ont la même efficacité si les deux fonctionnent avec les mêmes dépôts thermiques.

Cela signifie que la substance n'a pas d'importance, la performance est indépendante et ne peut pas être augmentée en la modifiant.

La conclusion de l'analyse précédente est que le cycle carnot est le haut du processus thermodynamique idéalement réalisable. En pratique, il existe de nombreux facteurs qui diminuent l'efficacité, par exemple le fait que l'isolement n'est jamais parfait et aux stades adiabatiques, il y a en fait un échange calorique avec l'extérieur.

Dans le cas d'une voiture, le bloc moteur est chauffé. D'un autre côté, le mélange de gaz et d'air ne se comporte pas exactement comme un gaz idéal, qui est le point de départ du cycle carnot. Ceci pour ne mentionner que certains facteurs qui entraîneront une réduction drastique des performances.

Exemples

Un piston à l'intérieur d'un cylindre

Si le système est un piston verrouillé dans un cylindre comme sur la figure 4, le piston augmente pendant l'expansion isotherme, comme on peut le voir dans le premier schéma de l'extrême gauche et augmente également pendant l'expansion adiabatique.

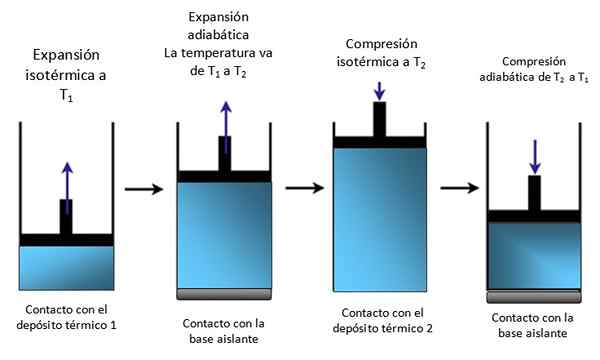Figure 4. Mouvement d'un piston à l'intérieur d'un cylindre. Source: auto-faite.

Puis isothermiquement compressé, donnant de la chaleur et continue de comprimer adiabatiquement. Le résultat est un mouvement dans lequel le piston monte et descend à l'intérieur du cylindre et peut être transmis à d'autres parties d'un appareil particulier, comme un moteur de voiture par exemple, qui produit une paire ou une machine torride.

Divers processus réversibles

En plus de l'expansion et de la compression d'un gaz idéal à l'intérieur d'un cylindre, il existe d'autres processus réversibles idéaux avec lesquels un cycle de carnot peut être configuré, par exemple:

- Mouvements aller-retour en l'absence de frottement.

- Un ressort idéal comprimé et décompressé et qui ne se déforme jamais.

- Circuits électriques dans lesquels il n'y a pas de résistance qui dissipe l'énergie.

- Cycles de magnétisation et de démagnétisation dans lesquels il n'y a pas de pertes.

- Chargement et téléchargement d'une batterie.

Une centrale nucléaire

Bien qu'il s'agisse d'un système très complexe, une première approche de ce qui est nécessaire pour produire de l'énergie dans le réacteur nucléaire est celle qui suit:

- Une source thermique, composée d'un matériau qui se désintégre radioactivement comme l'uranium.

Peut vous servir: modèle atomique actuel

- L'évier ou le dépôt thermique froid qui serait l'atmosphère.

- La "machine Carnot" qui utilise un fluide, presque toujours de l'eau courante, qui est fournie de la chaleur de la source thermique pour la transformer en vapeur.

Lorsque le cycle est effectué, l'électricité est obtenue comme un travail net. Lorsqu'elle est transformée en vapeur à haute température, l'eau est atteinte à une turbine, où l'énergie est transformée en mouvement ou en énergie cinétique.

La turbine active à son tour un générateur électrique qui transforme l'énergie de son mouvement en électricité. En plus des matériaux d'impassement tels que l'uranium, les combustibles fossiles peuvent bien sûr être utilisés comme source de chaleur.

Exercices résolus

-Exemple 1: Efficacité d'une machine thermique

L'efficacité d'une machine thermique est définie comme le rapport entre le travail de sortie et le travail d'entrée, et est donc une quantité sans dimension:

Efficacité maximale = (q_entrée - Q _sortie) / Q_entrée

Indiquant une efficacité maximale comme e_max, Il est possible de démontrer sa dépendance à la température, qui est la variable la plus simple à mesurer, comme:

et_max = 1 - (t₂/ T₁)

Où t₂ C'est la température de l'évier et t₁ C'est la température de la source thermique. Comme ce dernier est plus grand, l'efficacité se révèle toujours inférieure à 1.

Supposons qu'une machine thermique soit capable de travailler sur les moyens suivants: a) entre 200 K et 400 K, b) entre 600 K et 400 K. Quelle est l'efficacité dans chaque cas?

Solution

a) Dans le premier cas, l'efficacité est:

et_Max1 = 1 - (200/400) = 0.cinquante

b) Pour le deuxième mode, l'efficacité sera:

et_Max2 = 1- (400/600) = 0.33

Bien que la différence de température soit la même entre les deux modes, l'efficacité n'est pas. Et encore plus notable est que le mode le plus efficace fonctionne à une température plus basse.

-Exemple 2: chaleur absorbée et chaleur cédée

Une machine thermique de 22% produit 1530 J de travail. Trouver: a) La quantité de chaleur absorbée par le dépôt thermique 1, b) la quantité de chaleur jetée au réservoir thermique 2.

a) Dans ce cas, la définition d'efficacité est utilisée, car les travaux effectués, et non des températures des dépôts thermiques sont disponibles. 22% l'efficacité signifie que e _Max = 0.22, donc:

Efficacité maximale = travail / q_entrée

La quantité de chaleur absorbée est précisément Q_entrée, Tellement effaçant que vous avez:

Q_entrée = Travail / efficacité = 1530 J / 0.22 = 6954.5 J

b) La quantité de chaleur affectée au réservoir le plus froid est de δW = q_entrée - Q_sortie

Q_sortie = Q_entrée - ΔW = 6954.5 -1530 J = 5424.5 J.

Une autre façon vient de et_max = 1 - (t₂/ T₁). Comme les températures ne sont pas connues, mais celles-ci sont liées à la chaleur, l'efficacité peut également être exprimée comme suit:

et_max = 1 - (Q_Scèsement/ Q_absorbé)

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill. 654-657
2. Énergie nucléaire. Fonctionnement d'une centrale nucléaire. Récupéré de: énergie-nucléaire.filet
3. SERAY, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7e. Élégant. Cengage Learning. 618-622.
4. Tippens, P. 2011. Physique: concepts et applications. 7e édition. Colline de MacGraw. 414-416.
5. Walker, J.2008. La physique. 4e ed.Addison Wesley. 610-630