Processus de cycle de Brayton, efficacité, applications, exercices

Il Cycle de Brayton Il s'agit d'un cycle thermodynamique composé de quatre processus et s'applique à un liquide thermodynamique compressible comme un gaz. Sa première mention date de la fin du XVIIIe siècle, bien qu'il ait passé quelque temps avant qu'il ne soit élevé par James Joule. C'est pourquoi il est également connu sous le nom de Joule Cycle.

Il se compose des étapes suivantes, qui sont facilement illustrées dans le diagramme de pression - volume de la figure 1: compression adiabatique (aucune chaleur n'est échangée), une expansion isobare (se produit à pression constante), une expansion adiabatique (aucune chaleur n'est échangée) et une compression isobare et isobare (se produit à pression constante).

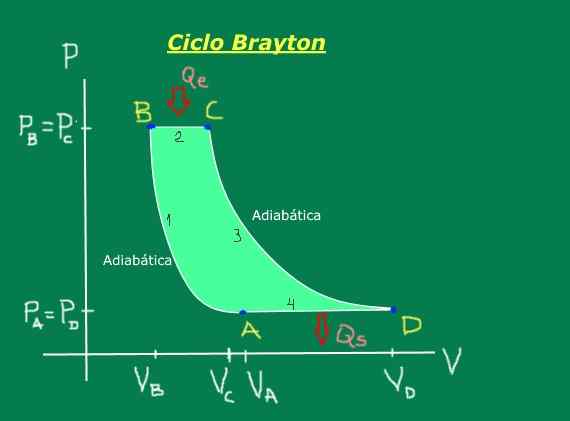Figure 1. Cycle de Brayton. Source: auto-faite.

[TOC]

Processus et description

Le cycle de Brayton est le cycle thermodynamique idéal qui est le mieux appliqué pour expliquer le fonctionnement thermodynamique des turbines à gaz et mélange le carburant à l'air, utilisé pour la production d'électricité et dans les moteurs aéronautiques.

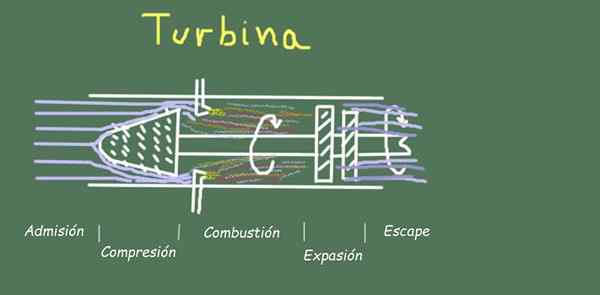Figure 2. Schéma de turbine et étapes de flux. Source: auto-faite.

Par exemple, dans le fonctionnement d'une turbine, il y a plusieurs étapes dans l'écoulement du gaz de fonctionnement, que nous verrons ci-dessous.

Admission

Il se compose de l'entrée d'air à la température et à la pression environnementale due à l'ouverture de la turbine.

Compression

L'air est comprimé par des palettes de rotation contre d'autres fixées dans la section du compresseur de la turbine. Cette compression est si rapide qu'il n'y a pratiquement pas d'échange de chaleur, il est donc modélisé par le processus de Brayton Cycle AB. L'air à la sortie du compresseur a augmenté sa pression et sa température.

La combustion

L'air est mélangé avec du gaz propane ou du carburant en poudre qui est introduit par les injecteurs de la chambre de combustion. Le mélange produit une réaction de combustion chimique.

Cette réaction est celle qui fournit la chaleur qui augmente la température et l'énergie cinétique des particules de gaz qui se développent dans la chambre de combustion à pression constante. Dans le cycle de Brayton, cette étape est modélisée avec le processus BC qui se produit à une pression constante.

Expansion

Dans la section de la turbine elle-même, l'air continue de se développer contre les palettes de turbine pour la faire tourner et produire des travaux mécaniques. Dans cette étape, l'air baisse sa température mais sans échanger de la chaleur pratiquement avec l'environnement.

Dans le cycle de Brayton, cette étape est simulée comme un processus de processus d'extension adiabatique. Une partie des travaux de la turbine est transférée au compresseur et l'autre est utilisée pour déplacer un générateur ou une hélice.

Échappement

L'air sortant est sous une pression constante égale à l'environnement et donne de la chaleur à l'énorme masse d'air externe, donc en peu de temps, il faut la même température d'air d'entrée. Dans le cycle de Brayton, cette étape est simulée avec le processus de pression constante, fermant le cycle thermodynamique.

Efficacité basée sur la température, la chaleur et la pression

Nous proposons de calculer l'efficacité du cycle Brayton, pour lequel nous commençons à partir de la définition de la même.

Dans une machine thermique, l'efficacité est définie comme le travail net effectué par la machine divisée par l'énergie thermique fournie.

Il peut vous servir: réflexion légère

Le premier principe de la thermodynamique établit que la chaleur nette contribuée à un gaz dans un processus thermodynamique est égale à la variation de l'énergie interne du gaz plus le travail effectué par le même.

Mais dans un cycle complet, la variation de l'énergie interne est nulle, il a donc que la chaleur nette contribuée dans le cycle soit égale au travail net effectué.

Chaleur entrante, chaleur sortante et efficacité

L'expression précédente nous permet d'écrire l'efficacité basée sur la chaleur absorbée ou entrante (POSITVO) et la chaleur assignée ou les QS sortants (négatif).

Chaleur et pression dans le cycle de Brayton

Dans le cycle de Brayton, la chaleur entre dans le processus isobare de la Colombie-Britannique et sort dans le processus isobare.

En supposant que non de pression constante qui est fournie avec une chaleur sensible que dans le processus de BC, puis sa température augmente de la tuberculose à TC selon la relation suivante:

Où cp C'est la capacité thermique à pression constante.

La chaleur sortante QS Il peut être calculé de manière similaire par la relation suivante qui s'applique au processus à une pression constante donne:

Remplacement de ces expressions dans l'expression qui nous donne une efficacité basée sur la chaleur entrante et la chaleur sortante, ce qui rend les simplifications pertinentes La relation suivante pour l'efficacité est obtenue:

Résulte que l'efficacité est indépendante de la masse d'air qui passe par la turbine.

Résultat simplifié

Il est possible de simplifier le résultat précédent si nous prenons en compte Pa = pd et que Pb = pc Étant donné que les processus AD et BC sont isobárica, c'est-à-dire à la même pression.

De plus, comme les processus AB et CD sont adiabatiques, la relation de Poisson pour les deux processus est remplie:

Où Gamma représente le quotient adiabatique, c'est-à-dire le quotient entre la capacité de chaleur à une pression constante et la capacité thermique à volume constant.

En utilisant ces relations et la relation de l'équation de l'État d'un gaz idéal, nous pouvons obtenir une expression alternative pour la relation de Poisson:

Comme nous savons que Pa = pd et que Pb = pc Remplacement et division membre en membre, la relation suivante entre les températures est obtenue:

Si chaque membre de l'équation précédente est soustrait de l'unité, la différence est résolue et les termes sont fixes, il peut être démontré que:

Afin que l'efficacité puisse être écrite en fonction de la température de l'air à l'entrée et de la température de l'air à la fin du processus de compression AB.

Performance en fonction du rapport de pression

L'expression obtenue pour l'efficacité du cycle Brayton en fonction des températures peut être réécrite pour être formulée en fonction du rapport de pression à la sortie et l'entrée du compresseur.

Ceci est réalisé si la relation de Poisson entre les points A et B est connue en fonction de la pression et de la température, obtenant que l'efficacité du cycle est exprimée comme suit:

Il peut vous servir: pression relative: formule, comment elle est calculée, exemples, exercice

Être r le quotient entre PB et PA.

Un rapport de pression typique est de 8. Dans ce cas, le cycle Brayton a une performance théorique de 45%.

Applications

Le cycle Brayton en tant que modèle s'applique aux turbines à gaz utilisées dans les usines thermoélectriques afin de déplacer les générateurs qui produisent de l'électricité.

Il s'agit également d'un modèle théorique qui s'adapte bien au fonctionnement des moteurs turbohériques qui sont utilisés dans les avions, mais il n'est pas applicable du tout dans les turborecteurs d'avion.

Quand il est intéressé.

figure 3. Turbofan Motor plus efficace que le turborecteur. Source: Pixabay

Dans les turboreacteurs d'avion, en revanche, il n'est pas intéressé.

Au contraire, il est intéressé.

Exercices résolus

-Exercice 1

Une turbine à gaz utilisée dans les usines thermoélectriques a une pression à la prise de compresseur de 800 kPa. La température du gaz entrant est l'environnement et est 25 Celsius, et la pression est de 100 kPa.

Dans la chambre de combustion, la température monte à 1027 Celsius pour entrer dans la turbine.

Déterminez l'efficacité du cycle, la température du gaz hors du compresseur et la température du gaz à la sortie de la turbine.

Solution

Comme nous avons la pression de gaz à la sortie du compresseur et nous savons que la pression d'entrée est la pression atmosphérique, il est donc possible d'obtenir le rapport de pression:

R = PB / PA = 800 kPa / 100 kPa = 8

Comme le gaz avec lequel la turbine fonctionne est un mélange d'air et de gaz propane, le coefficient adiabatique pour un gaz diatomique idéal est ensuite appliqué, c'est-à-dire un gamma de 1,4.

L'efficacité serait alors calculée comme ceci:

Où nous avons appliqué la relation qui donne l'efficacité du cycle Brayton en fonction du rapport de pression dans le compresseur.

Calcul de la température

Pour déterminer la température à la sortie du compresseur, ou quelle est la même température à laquelle le gaz pénètre dans la chambre de combustion, nous appliquons le rapport relationnel avec l'entrée du compresseur et les températures de sortie.

Si nous effacons la température TB de cette expression, nous obtenons:

En d'autres termes, la température pré-combustion est de 804,12 Celsius.

À mesure que l'exercice de l'exercice, nous devons après la combustion, la température s'élève à 1027 Celsius, pour entrer dans la turbine. Une partie de l'énergie thermique du gaz est utilisée pour déplacer la turbine, de sorte que la température à sa sortie doit être inférieure.

Peut vous servir: applications de l'énergie, de l'énergie, de la force, des concepts de travail

Pour calculer la température à la sortie de la turbine, nous utiliserons un rapport entre la température auparavant:

De là, nous nettoyons TD pour obtenir la température à la sortie de la turbine. Après avoir effectué les calculs, la température obtenue est:

TD = 143,05 Celsius.

-Exercice 2

Une turbine à gaz suit le cycle Brayton. Les pressions entre le départ et l'entrée du compresseur sont 12.

Supposons la température ambiante de 300 K. En tant que données supplémentaires, on sait que la température du gaz après la combustion (avant l'entrée de la turbine) est de 1000K.

Déterminez la température à la sortie du compresseur et la température à la sortie de la turbine. Déterminez également combien de kilogrammes de gaz circulent à travers la turbine à chaque seconde, sachant que sa puissance est de 30 kW.

Supposons la chaleur spécifique de gaz comme constante et prenez la valeur de celle-ci à température ambiante: CP = 1 0035 J / (kg k).

Supposons également que l'efficacité de compression dans le compresseur et la décompression de la turbine sont à 100%, ce qui est une idéalisation car en pratique les pertes se produisent toujours.

Solution

Pour déterminer la température à la sortie du compresseur, connu la température à l'entrée, nous devons nous rappeler qu'il s'agit d'une compression adiabatique, donc la relation de Poisson pour le processus AB peut être appliquée.

De cette façon, nous obtenons que la température TB à la sortie du compresseur est donnée par:

De la même manière, la décompression des gaz qui traversent la turbine, est un processus adiabatique qui correspondrait au processus du cycle de Brayton. Par conséquent, nous pouvons appliquer le rapport de Poisson pour obtenir la température de sortie de la turbine.

Pour tout cycle thermodynamique, le travail net sera toujours égal à la chaleur nette échangée dans le cycle.

Dans la relation précédente qui est la chaleur entrante (positive) et QS la chaleur sortante (négative). Dans le cycle de Brayton, ces échanges se produisent les processus BC et DA, les deux Isobáricas.

Le travail net par cycle d'opération peut ensuite être exprimé en fonction de la masse de gaz qui circulait dans ce cycle et les températures.

Dans cette expression m C'est la masse de gaz qui circulait à travers la turbine dans un cycle d'opération et CP La chaleur spécifique.

Si nous prenons le dérivé par rapport au temps de l'expression précédente, nous obtenons la puissance moyenne nette en fonction du flux massique.

Clairière M, et remplacer les températures, la puissance et la capacité thermique du gaz Nous obtenons un débit massique de 1578,4 kg / s.

Les références

1. Alfaro, J. Cycles thermodynamiques. Récupéré de: FIS.Puc.CL.
2. Fernández J.F. Cycle de Brayton. Turbine à gaz. OU.T.N. (Mendoza). Récupéré de: Edutecne.UTN.Édu.ardente.
3. Université de Séville. Département de physique. Cycle de Brayton. Récupéré de: Laplace.nous.est.
4. Université nationale expérimentale de la Táchira. Phénomène de transport. Cycles de gaz. Récupéré de: Unet.Édu.aller.
5. Wikipédia. Cycle de Brayton. Récupéré de: wikiwand.com
6. Wikipédia. Turbine à gaz. Récupéré de: wikiwand.com.