Chocs élastiques dans une dimension, cas spéciaux, exercices

Les chocs élastiques o Les collisions élastiques consistent en des interactions brèves mais intenses entre les objets, dans lesquels la quantité de mouvement et l'énergie cinétique sont préservées. Les Choques sont des événements très fréquents dans la nature: des particules subatomiques aux galaxies, passant par des balles de billard et des voitures de choc dans les parcs d'attraction, tous sont des objets capables de collision.

Pendant une collision ou un choc, les forces d'interaction entre les objets sont très intenses, bien plus que celles qui peuvent agir à l'extérieur. De cette façon, on peut affirmer que pendant la collision, les particules forment un système isolé.

Les collisions entre les balles de billard peuvent être considérées comme élastiques. Source: Pixabay.

Dans ce cas, il est réalisé que:

Où P C'est la quantité vectorielle de mouvement, dont l'ampleur est Mv (Speed ​​Mass). Si le dérivé de P est nul, cela signifie que P C'est constant. Et cela signifie qu'il ne varie pas, qu'il est conservé. Par conséquent, nous pouvons affirmer que:

P_soit = P_F

La quantité de mouvement P_soit avant la collision est la même qu'après collision. Ceci est rempli pour toute collision de type, à la fois élastique et inélastique.

Vous devez maintenant considérer ce qui suit: Pendant une collision, les objets éprouvent une certaine déformation. Lorsque le choc est élastique, les objets retrouvent rapidement leur forme d'origine.

[TOC]

Conservation de l'énergie cinétique

Normalement, lors d'un choc, une partie de l'énergie des objets est dépensée dans la chaleur, la déformation, le son et parfois même pour produire de la lumière. L'énergie cinétique du système après la collision est donc inférieure à l'énergie cinétique d'origine.

Lorsque l'énergie cinétique K, elle est alors conservée:

K_soit = K_F

Ce qui signifie que les forces agissant pendant la collision sont conservatrices. Alors que la collision dure l'énergie cinétique est brièvement transformée en énergie potentielle, puis c'est une énergie cinétique à nouveau. Les énergies cinétiques respectives varient, mais la somme reste constante.

Les collisions parfaitement élastiques ne sont pas fréquentes, bien que les balles de billard soient une assez bonne approche, ainsi que des collisions qui se déroulent entre les molécules de gaz idéales.

Chocs élastiques dans une dimension

Examinons une collision de deux particules de cela dans une seule dimension; C'est-à-dire que les particules qui interagissent se déplacent, par exemple, le long de l'axe x. Supposons qu'ils aient des masses m₁ et m₂. Les vitesses initiales de chacun sont ou₁ et ou₂ respectivement. Les vitesses finales sont V₁ et V₂.

Nous pouvons nous passer de la notation vectorielle, car le mouvement est effectué le long de l'axe x, cependant, les signes (-) et (+) indiquent la signification du mouvement. À gauche est négatif et à droite positive, par convention.

Peut vous servir: réseaux bravais: concept, caractéristiques, exemples, exercices

-Formules pour les collisions élastiques

Pour la quantité de mouvement

m₁ou₁ + m₂ou₂ = m₁V₁ + m₂V₂

Pour l'énergie cinétique

½ m₁ou²₁ + ½ m₂ou²₂ = ½ m₁V²₁ +  ½ m₂V²₂

Chaque fois que les masses et les vitesses initiales sont connues, il est possible de regrouper les équations pour trouver les vitesses finales.

Le problème est qu'en principe, c'est nécessaire. L'idéal serait de trouver des expressions qui ne les contiennent pas.

La première est de se passer du facteur ½ et de réorganiser les deux équations de telle manière qu'un signe négatif apparaît et que les masses peuvent être facteurs:

m₁ou₁ - m₁V₁ = M₂V₂ - m₂ou₂

m₁ou²₁ - m₁V²₁  = + M₂V²₂ - m₂ou²₂

Exprimé de cette manière:

m₁(ou₁ - V₁ ) = m₂(V₂ - ou₂)

m₁(ou²₁ - V²₁ ) = m₂ (V²₂ - ou²₂)

Simplification pour éliminer les carrés des vitesses

Maintenant, vous devez utiliser le produit notable, il ajoute à sa différence dans la deuxième équation, qui obtient une expression qui ne contient pas les carrés, comme à l'origine recherché:

m₁(ou₁ - V₁ ) = m₂(V₂ - ou₂)

m₁(ou₁ - V₁ ) (ou₁ + V₁ ) = m₂ (V₂ - ou₂) (V₂ + ou₂)

L'étape suivante consiste à remplacer la première équation dans la seconde:

m₂(V₂ - ou₂) (ou₁ + V₁ ) = m₂ (V₂ - ou₂) (V₂ + ou₂)

Et quand le terme est répété m₂(V₂ - ou₂) Des deux côtés de l'égalité, ce terme est annulé et est comme ceci:

(ou₁ + V₁) = (V₂ + ou₂)

Ou encore mieux:

ou₁ - ou₂= V₂ -  V₁

Vitesses finales V₁ et V₂ des particules

Maintenant, il y a deux équations linéaires avec lesquelles il est plus facile de travailler. Nous les replacerons en dessous de l'autre:

m₁ou₁ + m₂ou₂ = m₁V₁ + m₂V₂

ou₁ - ou₂= V₂ -  V₁

Multiplier la deuxième équation par m₁ Et l'ajout de terme à des restes de terme:

m₁ou₁ + m₂ou₂ = m₁V₁ + m₂V₂

m₁ou₁ - m₁ou₂= m₁V₂ - m₁ V₁

-

2 m₁ou₁ + (m₂ - m₁) ou₂ = (m₂ + m₁) V₂

Et il est déjà possible de dégager V₂. Par exemple:

Un traitement similaire peut être effectué pour trouver une équation pour V₁. Le lecteur est laissé comme un exercice pour démontrer que:

Cas spéciaux dans les collisions élastiques

Maintenant que les équations sont disponibles pour les vitesses finales des deux particules, il est temps d'analyser certaines situations spéciales.

Deux masses identiques

Dans ce cas m₁ = m₂ = m et:

V₁ = u₂

V₂ = u₁

Les particules échangent simplement leurs vitesses après collision.

Deux masses identiques, dont l'une était initialement au repos

De nouveau  m₁ = m₂ = m et en supposant que ou₁ = 0:

V₁ = u₂

V₂ = 0

Après l'accident, la particule qui était au repos acquiert la même vitesse de la particule qui se déplaçait, et elle s'arrête à son tour.

Peut vous servir: pression hydraulique

Deux masses différentes, l'une d'entre elles initialement au repos

Dans ce cas, supposons ou₁ = 0, Mais les masses sont différentes:

Et qu'est-ce qui se passerait si m₁ est beaucoup plus grand que m₂?

Il arrive que m₁ Rester au repos et m₂ Il est retourné avec la même vitesse avec laquelle il a eu un impact.

Coefficient ou règle de restitution de Huygens-Newton

Auparavant, la relation suivante entre les vitesses de deux objets en collision élastique a été déduite: ou₁ - ou₂ = V₂ -  V₁. Ces différences sont les vitesses relatives avant et après la collision. En général, pour une collision, il est réalisé que:

ou₁ - ou₂ = - (V₁ -  V₂)

Le concept de vitesse relative est mieux apprécié si le lecteur imagine qu'il se trouve sur l'une des particules et de cette position observe la vitesse à laquelle l'autre particule se déplace. L'équation précédente est réécrite comme ceci:

Si l'énergie cinétique n'est pas conservée, alors le quotient indiqué sera inférieur à 1. Appelons et à la valeur dudit quotient sans dimension:

Ou bien:

La valeur de et est entre 0 et 1 et est appelé coefficient de restitution. Lorsque le choc est élastique, E = 1. Lorsqu'il est totalement inélastique, E = 0, alors que s'il a une autre valeur intermédiaire, une certaine énergie cinétique s'est dispersée dans d'autres types d'énergie.

Exercices résolus

-Exercice résolu 1

Une balle de billard se déplace vers la gauche à 30 cm / s, entrant en collision avec une autre balle identique qui se déplace vers la droite à 20 cm / s. Les deux balles ont la même pâte et l'accident est parfaitement élastique. Trouvez la vitesse de chaque balle après impact.

Solution

ou₁ = -30 cm / s

ou₂ = +20 cm / s

C'est le cas particulier que deux masses identiques entrent en collision dans une dimension élastique, donc les vitesses sont échangées.

V₁ = +20 cm / s

V₂ = -30 cm / s

-Exercice résolu 2

Le coefficient de restitution d'une balle qui rebondit sur le sol est égal à 0,82. Si vous tombez du repos, quelle fraction de votre hauteur d'origine atteindra le ballon après avoir rebondi une fois? Et après 3 rebonds?

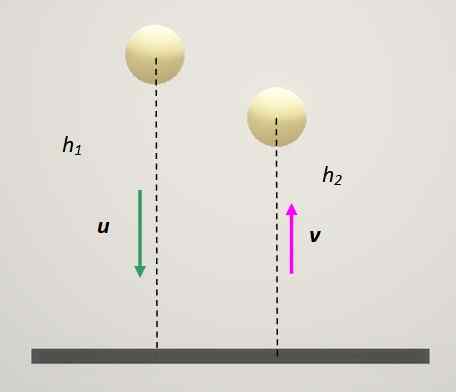Une balle rebondit contre une surface ferme et perd de la hauteur à chaque rebond. Source: auto-faite.

Solution

Le sol peut être objet 1 dans l'équation du coefficient de restitution. Et c'est toujours au repos, de sorte que:

La direction négative est choisie et le positif. La vitesse d'un objet qui est librement libéré d'une certaine hauteur H_soit est:

Le signe (-) indique que la balle descend:

Il peut vous servir: Torricelli Expérience: mesures de pression atmosphérique, importance

 

Avec cette vitesse rebondissant:

 

Le signe + indique qu'il s'agit d'une vitesse ascendante. Et selon lui, la balle atteint une hauteur maximale de:

 

Maintenant, il revient à nouveau au sol avec une vitesse de la même ampleur, mais le signe opposé:

Et rebondit avec:

Cela atteint une hauteur maximale de:

Rendez-vous à nouveau sur le sol avec:

Rebonds successifs

Chaque fois que la balle rebondit et monte, vous devez multiplier à nouveau la vitesse par 0.82:

Et atteint une hauteur maximale déterminée par le carré de ladite vitesse:

À ce stade h₃ est environ 30% de H_soit. Quelle serait la hauteur à 6e rebonds sans avoir à faire des calculs aussi détaillés que les précédents?

Serieuse H₆ = 0.82¹² H_soit = 0.092h_soit ou seulement 9% de H_soit.

-Exercice résolu 3

Un bloc de 300 g se déplace vers le nord à 50 cm / s et s'affronte contre un bloc de 200 g dirigé vers le sud 100 cm / s. Supposons que le choc est parfaitement élastique. Trouvez les vitesses après impact.

Données

m₁ = 300 g; ou₁ = + 50 cm / s

m₂ = 200 g; ou₂ = -100 cm / s

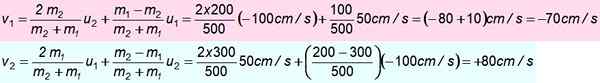
-Exercice résolu 4

Une masse de m est libérée₁ = 4 kg du point indiqué sur la piste sans frottement, jusqu'à ce qu'il entre en collision avec m₂ = 10 kg au repos. À quelle hauteur est m₁ Après la collision?

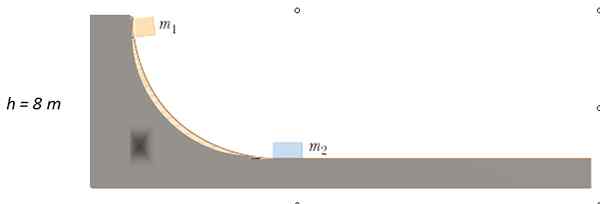
Solution

Puisqu'il n'y a pas de frottement, l'énergie mécanique est préservée pour trouver la vitesse ou₁ avec quoi m₁ impacts  m_2. L'énergie cinétique initialement est 0, puisque m₁ partie du reste. Lorsqu'il se déplaçant sur la surface horizontale, il n'a pas de hauteur, donc l'énergie potentielle est 0.

Mgh = ½ mu₁ ²

 

ou₂ = 0

Maintenant la vitesse de m₁ Après la collision:

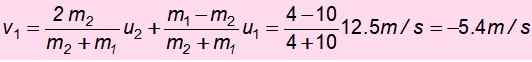
Le signe négatif signifie qu'il a été retourné. Avec cette vitesse, et l'énergie mécanique est à nouveau conservée pour trouver H ', La hauteur à laquelle il parvient à monter après l'accident:

½ mV₁² = mgh '

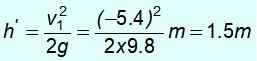
Notez que vous ne revenez pas au point de départ à 8 m de hauteur. Il n'a pas assez d'énergie car il a donné une partie de son énergie cinétique la masse m_1.

Les références

1. Giancoli, D.  2006. Physique: principes avec applications. 6^e. Ed Prentice Hall. 175-181
2. Rex, un. 2011. Fondamentaux de la physique. Pearson. 135-155.
3. SERAY, R., Vulle, c. 2011. Fondamentaux de la physique. 9^{n / A} Cengage Learning. 172 -182
4. Tipler, P. (2006) Physique de science et de technologie. 5e ed. Volume 1. Éditorial Revered. 217-238
5. Tippens, P. 2011. Physique: concepts et applications. 7e édition. Colline de MacGraw. 185 -195