Propriétés des cellules unitaires, constante rouge et types

La Cellule unitaire C'est un espace ou une région imaginaire qui représente l'expression minimale d'un tout; Que dans le cas de la chimie, l'ensemble serait un cristal composé d'atomes, d'ions ou de molécules, qui sont ordonnés à la suite d'un modèle structurel.

Dans la vie quotidienne, vous pouvez trouver des exemples qui incarnent ce concept. Pour cela, il est nécessaire de prêter attention aux objets ou aux surfaces qui présentent un certain ordre répétitif de ses éléments. Quelques mosaïques, bas-relief, artisanat.

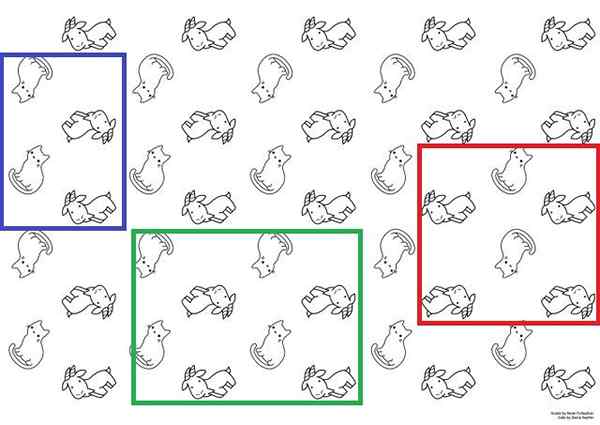Cellules unitaires sur papier chat et chèvre. Source: Hanna Petruschat (WMDE) [CC BY-SA 4.0 (https: // CreativeCommons.Org / licences / by-sa / 4.0)].

Pour l'illustrer plus clairement, vous avez l'image supérieure qui pourrait être utilisée comme papier de tapisserie. Dans ce document, les chats et les chèvres apparaissent avec deux sens alternatifs; Les chats sont des pieds ou de la tête, et les chèvres qui regardent ou descendent.

Ces chats et chèvres établissent une séquence structurelle répétitive. Pour construire tout le papier, il serait suffisant pour reproduire la cellule unitaire par la surface un nombre suffisant de fois, au moyen de mouvements de translation.

Les cellules unitaires possibles sont représentées avec les boîtes bleues, vertes et rouges. N'importe lequel de ces trois pourrait être utilisé pour obtenir le papier; Mais, il est nécessaire de les déplacer imaginairement le long de la surface pour savoir s'ils reproduisent la même séquence observée dans l'image.

En commençant par la boîte rouge, il serait apprécié que si trois colonnes (des chats et des chèvres) étaient déplacées vers la gauche, deux chèvres n'apparaîtraient plus dans sa partie inférieure mais une seule. Par conséquent, cela conduirait à une autre séquence et ne peut pas être considéré comme une cellule unitaire.

Tandis que s'ils déplacent imaginairement les deux boîtes, bleu et vert, la même séquence de papier serait obtenue. Les deux sont des cellules unitaires; Cependant, la boîte bleue obéit davantage à la définition, car elle est plus petite que la boîte verte.

[TOC]

Propriétés des cellules unitaires

Sa propre définition, en plus de l'exemple nouvellement expliqué, clarifie plusieurs de ses propriétés:

-S'ils se déplacent dans l'espace, quelle que soit la direction, le solide ou le verre complet sera obtenu. En effet, comme mentionné avec les chats et les chèvres, ils reproduisent la séquence structurelle; qui est égal à la distribution spatiale des unités répétitives.

-Ils doivent être aussi petits que possible (ou occuper peu de volume) par rapport aux autres options de cellules possibles.

Peut vous servir: acide méthylmalonique: structure, propriétés, synthèse, utilisations

-Ils sont ordinaires, symétriques. De même, sa symétrie se reflète littéralement dans les cristaux du composé; Si la cellule unitaire d'un sel est cubique, ses cristaux seront cubes. Cependant, il existe des structures cristallines décrites avec des cellules unitaires avec des géométries déformées.

-Ils contiennent les unités répétitives, qui peuvent être remplacées par des points qui, à leur tour, dimensionnellement ce qui est connu sous le nom de réticule. Dans l'exemple précédent, les chats et les chèvres représentent les points réticulaires, vus à partir d'un plan supérieur; c'est-à-dire deux dimensions.

Nombre d'unités répétitives

Les unités répétitives ou les points réticulaires des cellules unitaires maintiennent la même proportion de particules solides.

Si le nombre de chats et de chèvres est compté à l'intérieur de la boîte bleue, il y aura deux chats et chèvres. Il en va de même pour la boîte verte, et avec la boîte rouge aussi (même s'il est déjà connu que ce n'est pas une cellule unitaire).

Supposons par exemple que les chats et les chèvres sont respectivement des atomes G et C (un étrange soudage animal). Comme la proportion entre G et C est 2: 2 ou 1: 1 dans la boîte bleue, on peut s'attendre, sans erreurs, que le solide aura la formule GC (ou CG).

Lorsque le solide a des structures plus ou moins compactes, comme pour les sels, les métaux, les oxydes, les sulfures et les alliages, dans les cellules unitaires, il n'y a pas d'unités répétitives entières; c'est-à-dire qu'il y en a des parties ou des parties, qui s'ajoutent à une ou deux unités.

Ce n'est pas le cas pour GC. Si, la boîte bleue "commencerait" aux chats et aux chèvres en deux (1 / 2g et 1 / 2c) ou quatre parties (1/4G et 1 / 4C). Dans les sections suivantes, on verra que dans ces cellules unitaires, les points réticulaires sont commodément divisés de cette manière et d'autres.

Quelles constantes de réseau définissent une cellule unitaire?

Les cellules unitaires de l'exemple GC sont à deux dimensions; Cependant, cela ne s'applique pas dans les modèles réels qui considèrent les trois dimensions. Ainsi, les boîtes ou les parallélogrammes sont transformés en parallélépípédos. Maintenant, le terme "cellule" prend un plus grand sens.

Les dimensions de ces cellules ou parallélépipés dépendent de la durée de leurs côtés et angles respectifs.

Dans l'image inférieure, vous avez le coin arrière inférieur du parallélépipé, composé des côtés pour, b et c, et les angles α, β et γ.

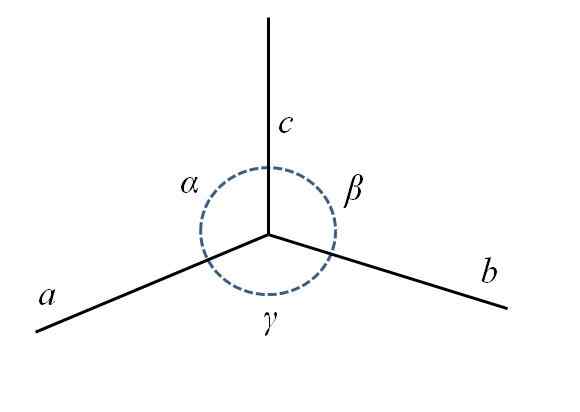Paramètres d'une cellule unitaire. Source: Gabriel Bolívar.

Comme tu peux le voir, pour est un peu plus long que b et c. Au centre, vous avez un cercle avec une ligne en pointillés pour indiquer les angles α, β et γ, entre CA, Cb et ba, respectivement. Pour chaque cellule unitaire, ces paramètres ont des valeurs constantes et définissent leur symétrie et le reste du verre.

Peut vous servir: peroxyde de calcium (CAO2): propriétés, risques et utilisations

En appliquant à nouveau un peu d'imagination, les paramètres d'image définiraient une cellule similaire à un cube étiré dans son bord pour. Ainsi, les cellules unitaires surgissent avec différentes longueurs et angles de ses bords, qui peuvent également être classés en différents types.

Gars

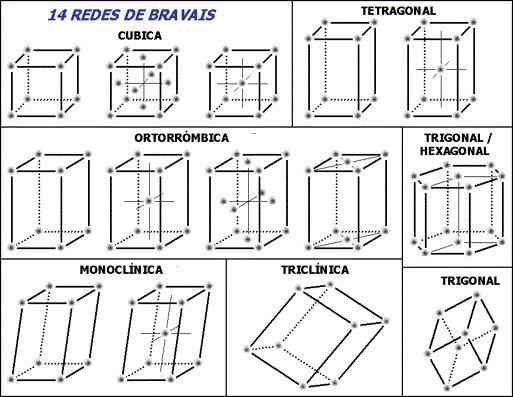
Les 14 réseaux Bravais et les sept systèmes cristallins de base. Source: Le versement d'origine était de l'ampleur de Wikipedia portugais. [CC BY-SA 3.0 (http: // CreativeCommons.Org / licences / by-sa / 3.0 /]]

Remarque pour démarrer les lignes pointillées à l'intérieur des cellules unitaires: elles indiquent l'angle arrière inférieur, comme expliqué. La question suivante peut être posée, où sont les points réticulaires ou les unités répétitives? Bien qu'ils donnent la mauvaise impression que les cellules sont vides, dans leurs sommets, la réponse réside.

Ces cellules sont générées ou choisis de telle manière que dans leurs sommets les unités répétitives se trouvent (points gris de l'image). Selon les valeurs des paramètres établis dans la section précédente, constante pour chaque cellule unitaire, sept systèmes cristallins sont dérivés.

Chaque système cristallin a sa propre cellule unitaire; Le second définit le premier. Dans l'image supérieure, il y a sept boîtes, correspondant aux sept systèmes cristallins; ou un peu plus de résumé, réseaux cristallins. Ainsi, par exemple, une cellule unitaire cubique correspond à l'un des systèmes cristallins qui définit un réseau cristallin cube.

Selon l'image, les systèmes ou réseaux cristallins sont:

-Cubique

-Tétragonal

-Ortorrombica

-Hexagonal

-Monoclinique

-Triclinique

-Trigone

Et dans ces systèmes cristallins, d'autres qui composent les quatorze filets de Bravais; que parmi tous les réseaux cristallins, ils sont les plus fondamentaux.

Cubique

Dans un cube, tous ses côtés et angles sont les mêmes. Par conséquent, ce qui suit est rempli dans cette cellule unitaire:

pour = b = c

α = β = γ = 90º

Il y a trois cellules unitaires cubes: simples ou primitives, centrées sur le corps (BCC) et centrées sur les faces (FCC). Les différences résident dans la façon dont les points (atomes, ions ou molécules) et dans le nombre d'entre eux sont distribués.

Laquelle de ces cellules est la plus compacte? Que dont le volume est plus occupé par les points: le cubique centré sur les visages. Notez que si nous remplaçons les points par les chats et les chèvres du début, ils ne se limiteraient pas à une seule cellule; Ils appartiendraient et seraient partagés par plusieurs. Encore une fois, ce serait des parties de G ou C.

Il peut vous servir: hydrocoloïde

Nombre d'unités

Si les chats ou les chèvres étaient dans les sommets, ils seraient partagés par 8 cellules unitaires; C'est-à-dire que chaque cellule aurait 1/8 de G ou C. Ensemble ou imaginez 8 cubes, en deux colonnes de deux lignes chacune, pour la visualiser.

Si les chats ou les chèvres étaient sur les visages, ils ne seraient partagés que par 2 cellules unitaires. Pour le voir, il suffit de rassembler deux cubes.

D'un autre côté, si le chat ou la chèvre étaient au centre du cube, ils n'appartienaient qu'à une seule cellule unitaire; La même chose se produit avec les boîtes de l'image principale, lorsque le concept a été abordé.

Dit alors ce qui précède, dans une simple cellule cubique ongle Point d'unité ou réticulaire, car il a 8 sommets (1/8 x 8 = 1). Pour la cellule cubique centrée dans le corps, vous avez: 8 sommets, ce qui est égal à un atome, et un point ou une unité au centre; Par conséquent, il y a deux unités.

Et pour la cellule cubique centrée sur les faces que vous avez: 8 sommets (1) et six faces, où la moitié de chaque point ou unité est partagé (1/2 x 6 = 3); Par conséquent, il a quatre unités.

Tétragonal

Des commentaires similaires peuvent être faits en ce qui concerne la cellule unitaire pour le système tétragonal. Ses paramètres structurels sont les suivants:

pour = b ≠ c

α = β = γ = 90º

Ortorrombica

Les paramètres de la cellule ortorrombique sont:

pour ≠ b ≠ c

α = β = γ = 90º

Monoclinique

Les paramètres de la cellule monoclinique sont:

pour ≠ b ≠ c

α = γ = 90º; β ≠ 90º

Triclinique

Les paramètres de la cellule triclinique sont:

pour ≠ b ≠ c

α ≠ β ≠ γ ≠ 90º

Hexagonal

Les paramètres de la cellule hexagonale sont:

pour = b ≠ c

α = β = 90º; γ ≠ 120º

En fait, la cellule constitue la troisième partie d'un prisme hexagonal.

Trigone

Et enfin, les paramètres de la cellule trigonale sont:

pour = b = c

α = β = γ ≠ 90º

Les références

1. Whitten, Davis, Peck & Stanley. (2008). Chimie. (8e Ed.). Cengage Learning P 474-477.
2. Fhiver & Atkins. (2008). Chimie inorganique. (Quatrième édition). Mc Graw Hill.
3. Wikipédia. (2019). Cellule primitive. Récupéré de: dans.Wikipédia.org
4. Bryan Stephanie. (2019). Cellule unitaire: paramètres latice et structures cubiques. Étude. Récupéré de: étudier.com
5. Centre de ressources académiques. (s.F.). Structures cristallines. [PDF]. Institut de technologie de l'Illinois. Récupéré de: Web.iit.Édu
6. Belford Robert. (7 février 2019). LATIQUES CRISTALES ET LES cellules unitaires. CHIMISTER BOOLISTexts. Récupéré de: Chem.Bibliothèque.org