Caractéristiques du rectangle

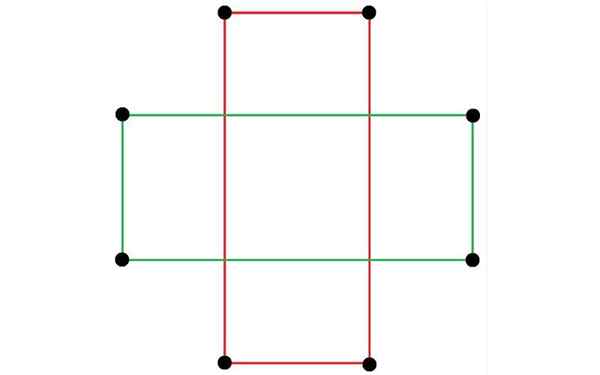
Deux rectangles. Source: Tomruen, CC BY-SA 4.0, Wikimedia Commons

Il rectangle Il se caractérise par un chiffre géométrique plat qui a quatre côtés et quatre sommets. De ces quatre côtés, une paire a la même mesure, tandis que l'autre paire a une mesure différente.

Cette figure est un polygone parallélogramme, car les côtés opposés d'un rectangle sont parallèles et ont les mêmes mesures. Les angles qui composent les rectangles ont une amplitude de 90 °, donc ce sont des angles droits. De là vient le nom de rectangle.

Le fait que les rectangles aient quatre angles de la même amplitude fait appeler ces figures géométriques Equiángulos.

Lorsqu'un rectangle est traversé par une ligne diagonale, deux triangles sont créés. Si un rectangle est croisé avec deux lignes diagonales, ils se croiseront au centre de la figure.

9 caractéristiques clés sur les rectangles

1. Nombre de côtés et de dimension

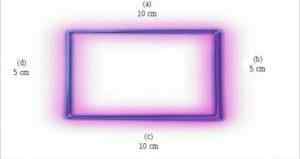
Les rectangles sont composés de quatre côtés. Nous pouvons diviser ces côtés en deux paires: une paire de côtés mesure la même chose, tandis que l'autre couple a des mesures plus élevées ou inférieures que le couple précédent.

Les côtés qui s'opposent ont les mêmes mesures, tandis que les côtés consécutifs ont des mesures différentes.

En plus de cela, les rectangles sont des figures à deux dimensions, ce qui signifie qu'ils n'ont que deux dimensions: large et haut.

Source: Wikipedia.org

2. Polygone

Les rectangles sont des polygones. En ce sens, les rectangles sont des figures géométriques, qui sont limitées par une ligne polygonale fermée (c'est-à-dire par un segment de ligne droite qui se ferme en soi).

Pour être plus précis, les rectangles sont des polygones quadrilatéraux, car ils ont quatre côtés.

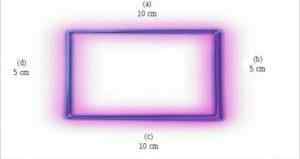
Il peut vous servir: triangle isocèle

3. Ce ne sont pas des polygones équilatéraux

Un polygone est équilatéral lorsque tous ses côtés mesurent le même. Les côtés d'un rectangle n'ont pas les mêmes mesures. Pour cette raison, on ne peut pas dire que les rectangles sont équilatéraux.

Source: Wikipedia.org

4. Polygone Equiangle

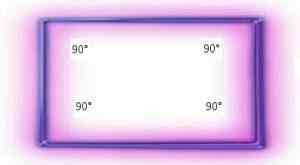
Les polygones d'Equiángulos sont ceux qui sont constitués d'angles qui ont la même amplitude.

Tous les rectangles sont composés de quatre angles droits (c'est-à-dire des angles de 90 °). Un rectangle de 10 cm x 20 cm aura quatre angles de 90 °, le même se produira avec un rectangle plus grand ou moindre.

Source: Wikipedia.org

5. La zone d'un rectangle

La zone d'un rectangle est égale au produit de la base par hauteur, la base étant le côté horizontal, tandis que la hauteur est le côté vertical. Une façon plus simple de le voir est de multiplier les mesures de deux côtés contiguës.

La formule pour calculer la zone de cette figure géométrique est:

a = b x a

Quelques exemples du calcul de la zone d'un rectangle sont:

- Rectangle avec une base de 5 cm et 2 cm de hauteur: 5 cm x 2 cm = 10 cm²

- Rectangle avec une base de 2 m et une hauteur de 0,5 m: 2 m x 0,5 m = 2 m²

- Rectangle avec 18 m et hauteur de 15 m: 18 m x 15 m = 270 m²

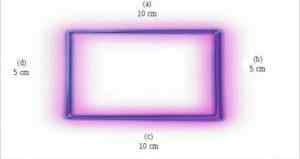Ce rectangle a une base de 10 cm et une hauteur de 5 cm. Votre zone sera le produit de 10 cm x 5 cm. Dans ce cas, la zone du rectangle est de 50 cm². Source: Wikipedia.org

6. Les rectangles sont des parallélogrammes

Les quadrilats peuvent être classés en trois types: trapézoïdes, trapézoïdes et parallélogrammes. Ces derniers sont caractérisés par deux paires de côtés parallèles, qui ne doivent pas nécessairement avoir les mêmes mesures.

En ce sens, les rectangles sont des parallélogrammes, puisque deux paires de côtés font face.

Peut vous servir: Équations de première dedexes: formule, comment les résoudre, exemple, exercices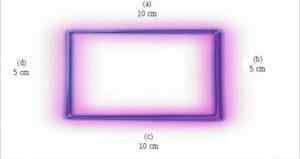Source: Wikipedia.org

7. Les angles opposés sont congruents et consécutifs sont complémentaires

Les angles opposés sont ceux trouvés dans les sommets non consécutifs de la figure. Alors que les angles consécutifs sont ceux qui sont adjacents, l'un à côté de l'autre.

Deux angles sont congruents quand ils ont la même amplitude. D'un autre côté, deux angles sont complémentaires lorsque la somme des amplitudes de ceux-ci produit un angle de 180 °, ou ce qui est le même, un angle plat.

Tous les angles d'un rectangle mesurent 90 °, il peut donc être dit que les angles opposés de cette figure géométrique sont congruents.

En ce qui concerne les angles consécutifs, le rectangle est composé d'angles de 90 °. Si les consécutifs sont ajoutés, le résultat sera de 180 °. Donc, ce sont des angles complémentaires.

8. Il se compose de deux triangles de rectangles

Si une diagonale est dessinée dans le rectangle (une ligne qui va d'un angle du rectangle à l'autre contraire), deux triangles rectangulaires sont obtenus. Ce type de triangle est celui qui est formé par un angle droit et deux angles aigus.

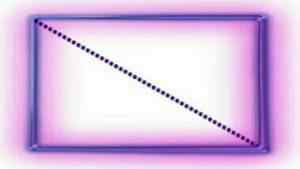La ligne de point représente la diagonale. Cela divise le rectangle en deux triangles. Source: Wikipedia.org

9. Les diagonales sont coupées à leur point médian

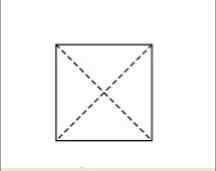
Comme déjà expliqué, les diagonales sont les lignes qui vont de l'un des angles à un autre angle opposé. Si deux diagonales sont dessinées dans le rectangle, elles se croiseront au milieu de la figure.

Les références

1. Rectangle. Récupéré de Mathisfun.com.
2. Rectangle. Récupéré de Merriam-Webster.com.
3. Propriétés des rhombus, des rectanges et des carrés. Les mannequins ont récupéré.com.
4. Rectangle. Récupéré de.Wikipédia.org.
5. Rectangle. Récupéré de Collinsdiction et.com.

Peut vous servir: inverse multiplicatif: explication, exemples, exercices résolus