Caractéristiques du carré

Un carré régulier. Avec licence

La principale Caractéristique du carré C'est le fait qu'il est formé par quatre côtés, qui ont exactement les mêmes mesures. Ces côtés sont organisés pour qu'ils forment quatre angles droits (90 °).

Il carré C'est une figure géométrique de base, un objet d'étude de la géométrie plate, car il s'agit d'une figure à deux dimensions (qui est large et grande, mais manque de profondeur).

Les carrés sont des polygones. D'une manière plus concrète, ce sont des polygones (a) quadrilatères pour avoir quatre côtés, (b) équilatéraux pour avoir des côtés qui mesurent le même et (c) les équilgulos pour avoir des angles avec la même amplitude.

Ces deux dernières propriétés du carré (équilatérale et equiangle) peuvent être résumées en un seul mot:. Cela signifie que les carrés sont des polygones quadrilatéraux réguliers.

Comme les autres figures géométriques, le carré a une zone. Cela peut être calculé en multipliant l'un de ses côtés par lui-même. Par exemple, si nous avons un carré qui mesure 4 mm, sa superficie sera de 16 mm².

Caractéristiques carrées

1. Nombre de côtés et de dimension

Les carrés sont composés de quatre côtés qui mesurent le même. De plus, les carrés sont des figures à deux dimensions, ce qui signifie qu'ils n'ont que deux dimensions: large et élevée.

2. Polygone

Les carrés sont des polygones. Cela signifie que les carrés sont des chiffres géométriques délimités par une ligne fermée formée par des segments de ligne consécutifs (ligne polygonale fermée).

Plus précisément, c'est un polygone quadrilatère car il a quatre côtés.

3. Polygone équilatéral

On dit qu'un polygone est équilatéral lorsque tous ses côtés ont la même mesure. Cela signifie que si un côté du carré mesure 2 mètres, tous les côtés mesurent 2 mètres.

Cela peut vous servir: que se passerait-il si la terre était plus proche du soleil?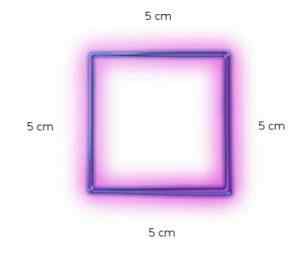

4. Polygone Equiangle

On dit qu'un polygone est équiangle lorsque tous les angles qui forment la ligne polygonale fermée ont la même mesure.

Tous les carrés sont composés de quatre angles droits (c'est-à-dire des angles de 90 °), peu importe.

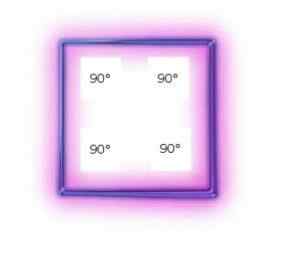
Tous les carrés sont equiangulos parce que leurs angles ont la même amplitude. C'est-à-dire 90 °.

5. Polygone régulier

Lorsqu'un polygone est équilatéral et en même temps Equiangle, il est considéré qu'il s'agit d'un polygone ordinaire.

Parce que le carré a des côtés qui mesurent les mêmes et les angles d'amplitude égale, on peut dire qu'il s'agit d'un polygone ordinaire.

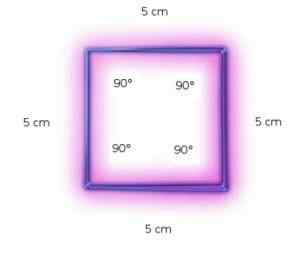
Les carrés ont les deux côtés d'une mesure égale et des angles d'amplitude égale, donc ce sont des polygones réguliers.

6. La zone d'un carré

La zone d'un carré est égale au produit d'un côté de l'autre. Parce que les deux côtés ont exactement la même mesure, la formule peut être simplifiée en disant que la zone de ce polygone est égale à l'un de ses côtés au carré, c'est-à-dire (côté)².

Quelques exemples du calcul de la zone d'un carré sont:

- Carré avec des côtés de 2 m: 2 m x 2 m = 4 m²

- Carrés avec des côtés de 52 cm: 52 cm x 52 cm = 2.704 cm²

- Carré avec 10 mm côtés: 10 mm x 10 mm = 100 mm²

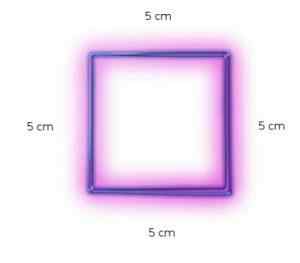
Le carré présenté dans l'image a des côtés de 5 cm.

Votre zone sera le produit de 5 cm x 5 cm, ou ce qui est le même (5 cm)²

Peut vous servir: hydrologie: ce qu'est l'histoire, quelles études

Dans ce cas, le carré du carré est de 25 cm²

7. Les carrés sont des parallélogrammes

Les parallélogrammes sont un type de quadrilatoral qui ont deux paires de côtés parallèles. Cela signifie que quelques côtés se font face, tandis que la même chose se produit avec l'autre couple.

Il existe quatre types de parallélogrammes: les rectangles, les rhombus, les rhomboïdes et les carrés.

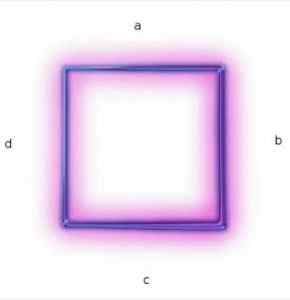
Les carrés sont des parallélogrammes car ils ont deux paires de côtés parallèles.

Les côtés (a) et (c) sont parallèles.

Les côtés (b) et (d) sont parallèles.

8. Les angles opposés sont congruents et consécutifs sont complémentaires

Que deux angles sont congrus signifie qu'ils ont la même amplitude. En ce sens, comme un carré a tous ses angles de même amplitude, on peut dire que les angles opposés sont congruents.

Pour sa part, le fait que deux angles consécutifs soient complémentaires signifie que la somme de ces deux est égale à un angle plat (celui qui a une amplitude de 180 °).

Les angles d'un carré sont des angles droits (90 °), donc sa somme de 180 °.

9. Ils sont construits à partir d'une circonférence

Pour construire un carré, une circonférence est dessinée. Par la suite, deux diamètres sont dessinés sur cette circonférence. Ces diamètres doivent être perpendiculaires, formant une croix.

Une fois les diamètres rédigés, nous aurons quatre points dans lesquels les segments de ligne ont coupé la circonférence. Si ces quatre points sont joints, un carré sera pris.

dix. Les diagonales sont coupées à leur point médian

Les diagonales sont des lignes droites qui sont tirées d'un angle à un autre qui est opposé. Dans un carré, deux diagonales peuvent être dessinées. Ces diagonales se croiseront au milieu du carré.

Peut vous servir: Recherche bibliographique: définition, types, techniques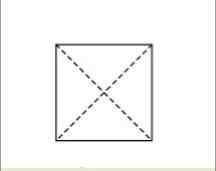

Dans l'image, les lignes pointillées représentent les diagonales. Comme on peut le voir, ces lignes se croisent exactement au milieu du carré.

Les références

1. Carré et ses propriétés. Récupéré de MathonpenRef.com
2. Propriétés des rhombus, des rectanges et des carrés. Les mannequins ont récupéré.com