Concept gratuit, équations, exercices résolus

La chute libre C'est le mouvement vertical qu'un objet éprouve lorsqu'il est tombé d'une certaine hauteur près de la surface de la terre. C'est l'un des mouvements les plus simples et les plus immédiats qui sont connus: en ligne droite et avec une accélération constante.

Tous les objets qui sont abandonnés ou qui sont jetés verticalement vers le haut ou vers le bas, se déplacent avec l'accélération de 9.8 m / s² fourni par la gravité de la terre, quelle que soit sa masse.

Chute libre d'une falaise. Source: Pexels.com.

Ce fait peut être accepté aujourd'hui sans problèmes. Cependant, comprendre la vraie nature de la chute libre a pris un certain temps. Les Grecs l'avaient déjà décrit et interprété très essentiellement vers le quatrième siècle un C.

[TOC]

Équations du mouvement de chute libre

Une fois convaincu que l'accélération est la même pour tous les corps libérés sous l'action de la gravité, il est temps d'établir les équations nécessaires pour expliquer ce mouvement.

Il est important de souligner que la résistance à l'air n'est pas prise en compte dans ce premier modèle de mouvement. Cependant, les résultats de ce modèle sont très précis et proches de la réalité.

Dans tout ce qui suit, le modèle de particules sera supposé, c'est-à-dire que les dimensions de l'objet ne sont pas prises en compte, en supposant que la masse entière est concentrée en un seul point.

Pour un mouvement rectiligne uniformément accéléré, il est pris comme un axe de référence à l'axe et. Le sens positif est repris et le négatif.

Les amplitudes cinématiques

De cette façon, les équations de la position, de la vitesse et de l'accélération selon le temps sont:

Accélération

A = g = -9.8 m / s² (-32 pieds / s²)

Position en fonction du temps: et T)

y = y_soit + V_soit . T + ½ GT²

Où et_soit C'est la position initiale du mobile et V_soit est la vitesse initiale. N'oubliez pas que dans le lancement vertical, la vitesse initiale est nécessairement différente de 0.

Qui peut être écrit comme:

et et_soit = V_soit . T + ½ GT²

Δy = v_soit . T + ½ GT²

Avec Δet Être le déplacement fabriqué par la particule mobile. Dans les unités du système international, la position et le déplacement sont donnés en mètres (m).

Vitesse en fonction du temps: V (t)

V = V_soit + g . t

Vitesse en fonction du déplacement

Il est possible de déduire une équation qui relie le déplacement avec la vitesse, sans temps intermédiaire. Pour ce faire, le temps de la dernière équation est effacé:

Peut vous servir: modèle mécanique quantique de l'atome

 Et il est remplacé dans l'équation de déplacement:

Δy = v_soit . T + ½ GT²

Le carré est développé à l'aide du produit remarquable et les termes sont regroupés.

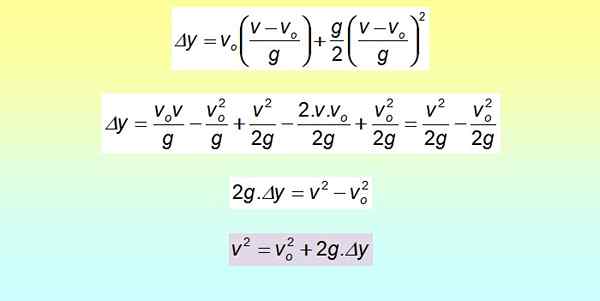
Cette équation est utile lorsque le temps n'est pas disponible, mais à la place, il y a des vitesses et des déplacements, comme on le verra dans la section des exemples résolus.

Exemples de chute libre

Le lecteur attentif aura remarqué la présence de la vitesse initiale V_soit. Les équations précédentes sont valables pour les mouvements verticaux sous l'action de la gravité, à la fois lorsque l'objet tombe d'une certaine hauteur, comme s'il était jeté verticalement vers le haut ou vers le bas.

Lorsque l'objet tombe, c'est simplement fait V_soit = 0 et les équations sont simplifiées comme suit.

Accélération

A = g = -9.8 m / s² (-32 pieds / s²)

Position en fonction du temps: et T)

y = y_soit+ ½ GT²

Vitesse en fonction du temps: V (t)

v = g . t

Vitesse en fonction du déplacement

V² = 2G. Dy

Dy Ce sera également négatif, car V² Ça doit être un montant positif. Cela se produira les deux si le Origine soit zéro du système de coordonnées au point de lancement ou au sol.

Si le lecteur le préfère, il peut prendre la direction vers le bas comme positif. La gravité continuera d'agir si on pense que c'est + 9.8 m / s². Mais vous devez être cohérent avec la convention des signes sélectionnée.

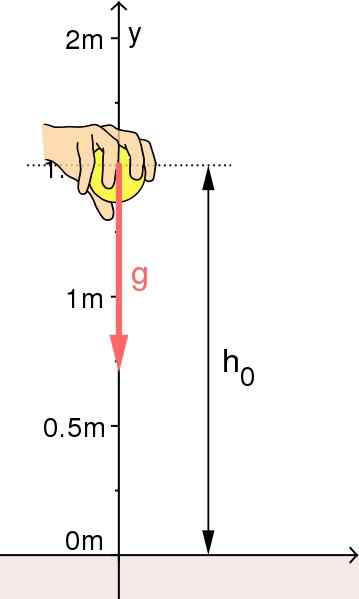Chute libre d'un objet: l'origine du système de référence a été sélectionnée au sol. Source: Source: Mikerun [CC BY-SA 4.0 (https: // CreativeCommons.Org / licences / by-sa / 4.0)]

Lancement vertical

Ici, naturellement, la vitesse initiale ne peut pas être nul. Nous devons fournir l'objet à une impulsion pour monter. Selon la vitesse initiale fournie, l'objet atteindra une hauteur supérieure ou moindre.

Bien sûr, il y aura un moment où l'objet s'arrête momentanément. Ensuite, la hauteur maximale aura été atteinte par rapport au point de lancement. L'accélération est également toujours en bas. Voyons ce qui se passe dans ce cas.

Calcul de la hauteur maximale atteinte

Choisir Me = 0:

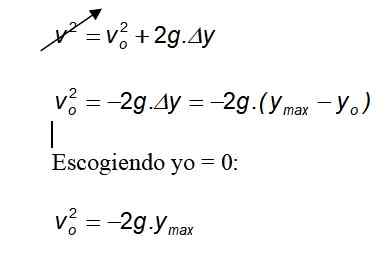
Comme la gravité pointe toujours le sol dans le sens négatif, le signe négatif est annulé.

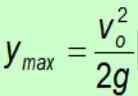
Calcul de temps maximum

Une procédure similaire sert à trouver le temps nécessaire à l'objet pour atteindre la hauteur maximale.

V = V_soit + g . t

Cela fait v = 0

V_soit = - g . t_Max

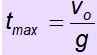
Le temps de vol est le moment où l'objet dure dans les airs. Si l'objet revient au point de départ, le temps de montée est égal au temps de descente. Par conséquent, le temps de vol est 2. T max.

Peut vous servir: échelle microscopique: propriétés, comptes de particules, exemples

Est deux fois le T_Max Le temps total que l'objet dure dans les airs? Oui, tant que l'objet part d'un point et y revient.

Si le lancement est effectué à partir d'une certaine hauteur sur le sol et que l'objet est autorisé à continuer à cela, le temps de vol ne sera plus le double de la durée maximale.

Exercices résolus

Dans la résolution des exercices qui suivent, les éléments suivants seront pris en compte:

1-la hauteur de l'endroit où l'objet est tombé est petit par rapport au rayon de la terre.

2-La résistance à l'air est méprisable.

3-La valeur de l'accélération de la gravité est de 9.8 m / s²

4-quand ce sont des problèmes avec un seul mobile, de préférence il est choisi et_soit = 0 au point de départ. Cela facilite généralement les calculs.

5-à moins que l'inverse est indiqué, la direction ascendante est considérée comme positive.

6 -Dans les mouvements combinés ascendant et descendants, les équations appliquées directement offrent les résultats corrects, tant que la cohérence est maintenue avec les signes: en haut, en baisse, négatif et gravité -9.8 m / s² ou -10 m / s² Si vous préférez vous-même (pour plus de confort lors du calcul).

Exercice 1

Une balle est lancée verticalement avec une vitesse de 25.0 m / s. Répondre aux questions suivantes:

a) Combien cela monte-t-il?

b) Combien de temps faut-il pour atteindre son point le plus élevé?

c) Combien de temps prend la balle pour toucher la surface de la terre après avoir atteint son point le plus élevé?

d) Quelle est votre vitesse lorsque vous revenez au niveau de l'endroit où il a commencé?

Solution

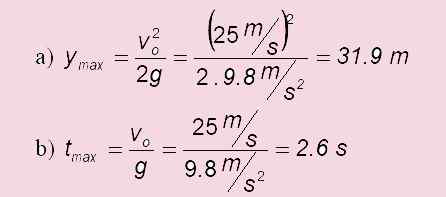
c) Dans le cas d'un lancement de niveau: t_vol = 2 . t_Max = 2 x6 s = 5.1 s

d) Lorsqu'il revient au point de départ, la vitesse a la même ampleur que la vitesse initiale mais la direction opposée, il doit donc être - 25 m / s. Il est facilement vérifié en remplaçant les valeurs dans l'équation pour la vitesse:

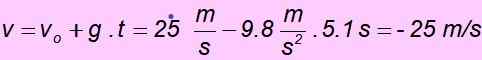
Exercice 2

Une petite valise postale est libérée d'un hélicoptère qui descend à une vitesse constante de 1.50 m / s. Après 2.00 s Calculez:

a) Quelle est la vitesse de la valise?

b) Jusqu'où se trouve la valise sous l'hélicoptère?

c) Quelles sont vos réponses pour les sections a) et b) si l'hélicoptère augmente à une vitesse constante de 1.50 m / s?

Solution

Section A

Lors de l'abandon de l'hélicoptère, la valise en transporte la vitesse initiale, donc V_soit = -1.50 m / s. Avec le temps indiqué, la vitesse a augmenté grâce à l'accélération de la gravité:

Peut vous servir: corps célestes

V = V_soit + g . t = -1.50 - (9.8 x 2) m / s = - 21.1 m / s

Section B

Voyons à quel point la valise est descendue par rapport au point de départ à ce moment-là:

Valise: Dy = v_soit . T + ½ GT² = -1.50 x 2 + ½ (-9.8) x 2² M = -22.6 m

Il a été sélectionné et_soit = 0 Au point de départ, comme indiqué au début de la section. Le signe négatif indique que la valise est descendue 22. 6 m en dessous du point de départ.

En attendant l'hélicoptère Il est tombé rapidement -1.50 m / s, nous supposons constamment, donc dans le temps indiqué de 2 secondes, l'hélicoptère a voyagé:

Hélicoptère: δy = V_soit.t = -1.cinquante x 2 m = -3 m.

Par conséquent, après 2 secondes, la valise et l'hélicoptère sont séparés par une distance par rapport à:

D =| -22.6 - (-3) | M = 19. 6 m.

La distance est toujours positive. Pour souligner ce fait, la valeur absolue est utilisée.

Section C

Lorsque l'hélicoptère augmente, il a une vitesse de + 1.5 m / s. Avec cette vitesse, la valise sort, de sorte qu'après 2 s transporte déjà:

V = V_soit + g . T = +1.50 - (9.8 x 2) m / s = - 18.1 m / s

La vitesse s'avère négative, car après 2 secondes, la valise se déplace vers le bas. A augmenté grâce à la gravité, mais pas autant que dans la section A.

Maintenant, nous trouverons combien la valise est descendue en ce qui concerne le point de départ au cours des 2 premières secondes de voyage:

Valija: δy = V_soit . T + ½ GT² = +1.50 x 2 + ½ (-9.8) x 2² M = -16 .6 m

Pendant ce temps, l'hélicoptère Il a augmenté Concernant le point de départ, et l'a fait à vitesse constante:

Hélicoptère: δy = V_soit.T = +1.cinquante x 2 m = +3 m.

Après 2 secondes, la valise et l'hélicoptère sont séparés par une distance de:

D =| -16.6 - (+3) | M = 19.6 m

La distance qui les sépare est la même dans les deux cas. La valise parcourt moins de distance verticale dans le deuxième cas, car sa vitesse initiale a été dirigée vers le haut.

https: // youtu.be / w2uvetxwsfk

Les références

1. Kirkpatrick, L. 2007. Physique: un regard sur le monde. 6^faire Édition abrégée. Cengage Learning.  23 - 27.
2. Rex, un. 2011. Fondamentaux de la physique. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14^e. Élégant. Volume 1. 50 - 53.
4. SERAY, R., Vulle, c. 2011. Fondamentaux de la physique. 9^{n / A} Élégant. Cengage Learning. 43 - 55.
5. Wilson, J. 2011. Physique 10. Pearson Education. 133 - 149.