Binomial conjugué comment il est résolu, exemples, exercices

UN Binôme conjugué D'un autre binôme est celui dans lequel ils ne diffèrent que par un signe de l'opération. Le binôme, comme son nom l'indique, est une structure algébrique qui se compose de deux termes.

Quelques exemples de binômes sont: (A + B), (3m - n) et (5x - y). Et leurs binômes conjugués respectifs sont: (a - b), (-3m - n) et (5x + y). Comme on peut le voir immédiatement, la différence est dans le signe.

Figure 1. Un binôme et son binôme conjugué. Ils ont les mêmes termes, mais diffèrent par le signe. Source: F. Zapata.

Un binôme multiplié par son conjugué se traduit par un produit remarquable qui est beaucoup utilisé en algèbre et en science. Le résultat de la multiplication est la soustraction des carrés des termes du binôme d'origine.

Par exemple, (X - y) C'est un binôme et son conjugué est (x + y). Ensuite, le produit des deux binômes est la différence des carrés des termes:

(X - y).(x + y) = x² - et²

[TOC]

Comment un binomial conjugué est-il résolu?

La règle énoncée avec les binômes conjugués est la suivante: 

Le produit de deux binômes conjugués est égal au carré du premier terme moins le carré du deuxième terme. Ce résultat est appelé la différence carrée.

À titre d'exemple d'application, nous commencerons par démontrer le résultat précédent, qui peut être fait en utilisant la propriété distributive du produit par rapport à la somme algébrique.

(x - y) (x + y) = x.x + x.et et.X - y.et

La multiplication précédente a été obtenue en suivant ces étapes:

- Le premier terme du premier binomial est multiplié par le premier terme du second

- Puis le premier du premier, pour la seconde de la seconde

- Puis le deuxième du premier pour le premier du second 

- Enfin le deuxième du premier pour le deuxième de la seconde.

Peut vous servir: algèbre vectorielle

Maintenant, faisons un petit changement à l'aide de la propriété commutative: et.x = x.et. Il reste comme ceci:

(x - y) (x + y) = x.x + x.y - x.et et.et

Comme il y a deux termes égaux mais autrement (mis en évidence en couleur et soulignés), ils sont annulés et simplifiés:

(x - y) (x + y) = x.X - y.et

Enfin, il est appliqué que la multiplication d'un nombre par elle-même est équivalente à le soulever carré, donc X.x = x² et aussi et.y = y².

De cette façon, ce qui avait été souligné dans la section précédente, que le produit d'une somme pour sa différence est la différence des carrés:

(X - y).(x + y) = x² - et²

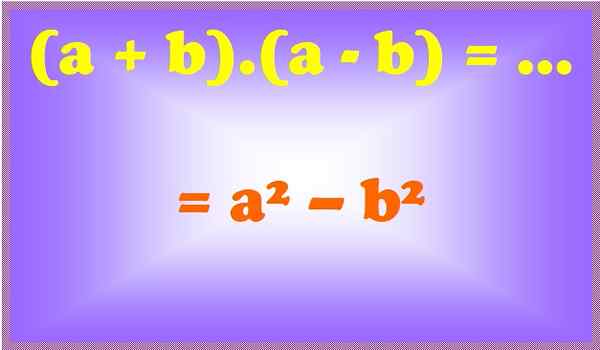Figure 2. Une somme pour sa différence est une différence de carrés. Source: F. Zapata.

Exemples

- Binômes conjugués de diverses expressions

Exemple 1

Trouver le conjugué de (et² - 3y).

Répondre: (et² + 3y)

Exemple 2

Obtenir le produit de (et² - 3y) pour son conjugué.

Répondre: (et² - 3y) (et² + 3y) = (et²)² - (3y)² = Y⁴ - 3² et² = Y⁴ - 9Y²

Exemple 3

Développer le produit (1 + 2a).(2a -1).

Répondre: L'expression précédente est équivalente à (2a + 1).(2a -1), c'est-à-dire qu'il correspond au produit d'un binôme pour son conjugué.

Il est connu que le produit d'un binôme pour son binôme conjugué est égal à la différence des carrés des termes binomiaux:

(2a + 1) (2a -1) = (2a)² - 1² = 4 a² - 1

Exemple 4

Écrivez le produit (x + y + z) (x - y - z) comme une différence de carrés.

Répondre: Nous pouvons assimiler les trinomiaux avant la forme de binômes conjugués, en faisant attentivement des parenthèses et des crochets:

(x + y + z) (x - y - z) = [x + (y + z)] [x - (y + z)]

De cette façon, la différence de carrés peut être appliquée:

(x + y + z) (x - y - z) = [x + (y + z)].[x - (y + z)] = x² - (Y + z)²

Exemple 5

Exprimer le produit (m² - M -1).(m² + m -1) comme différence de carrés.

Peut vous servir: 120 diviseurs

Répondre: L'expression précédente est le produit de deux trinomiaux. Tout d'abord, il doit être réécrit comme le produit de deux binômes conjugués:

(m² - m -1) (m² + m -1) = (m² - 1 - m) (m² -1 + m) = [(m² -1) - M].[(m² -1) + m)]

Nous appliquons le fait que le produit d'un binomial par son conjugué est la différence quadratique de ses termes, comme expliqué:

[(m² -1) - M].[(m² -1) + m)] = (m² -1)² - m²

Exercices

Comme toujours, il commence par les exercices les plus simples, puis le niveau de complexité augmente.

- Exercice 1

Escriba (9 - A²) En tant que produit.

Solution

Premièrement, nous réécrivons l'expression comme une différence de carrés, afin d'appliquer ce qui explique précédemment. Donc:

(9 - A²) = (3² - pour²)

Nous tenons immédiatement, ce qui équivaut à écrire cette différence de carrés en tant que produit, comme demandé dans l'énoncé:

(9 - A²) = (3² - pour²) = (3 + a) (3 -a)

- Exercice 2

Factoriser 16x² - 9Y⁴.

Solution

Facteur d'une expression signifie l'écrire comme un produit. Dans ce cas, il est nécessaire de réécrire précédemment l'expression, d'obtenir une différence de carrés.

Il n'est pas difficile de le faire, puisque observer attentivement, tous les facteurs sont des carrés parfaits. Par exemple 16 est le carré de 4, 9 est le carré de 3, et⁴ est le carré de et² et X² est le carré de X:

16x² - 9Y⁴  = 4²X² - 3²et⁴ = 4²X²  - 3²(et²)²

Ensuite, ce que nous savons déjà est appliqué: qu'une différence de carrés est le produit de binômes conjugués:

(4x)² - (3 et²)² = (4x - 3 et²) . (4x + 3 et²)

- Exercice 3

Écrire (A - B) en tant que produit binomial

Solution

La différence précédente doit être écrite comme des différences carrées

(√a)² -(√b)²

Alors il est appliqué que la différence de carrés est le produit des binômes conjugués

Peut vous servir: réduction de termes similaires

(√a - √b) (√a + √b)

- Exercice 4

L'une des utilisations du binomial conjugué est la rationalisation des expressions algébriques. Cette procédure consiste à éliminer les racines du dénominateur d'une expression fractionnaire qui, à de nombreuses occasions, facilite les opérations. Il est demandé d'utiliser le binôme conjugué pour rationaliser l'expression suivante:

√ (2 -x) / [√3 - √ (2 + x)]]]

Solution

La première consiste à identifier le binôme conjugué du dénominateur: [√3 + √ (2 + x)]]].

Maintenant, nous multiplions le numérateur et le dénominateur de l'expression d'origine par le binôme conjugué:

√ (2 -x) [√3 + √ (2 + x)] / [√3 - √ (2 + x)].[√3 + √ (2 + x)]

Dans le dénominateur de l'expression précédente, nous reconnaissons le produit d'une différence par une somme, que nous savons déjà qui correspond à la différence des carrés des binômes:

√ (2-x) .[√3 + √ (2 + x)] / (√3)² - [√ (2 + x)]² 

Simplifier le dénominateur est:

√ (2-x).[√3 + √ (2 + x)] / [3 - (2 + x)] = √ (2 -x). [√3 + √ (2 + x)] / (1 - x)

Maintenant, nous prenons soin du numérateur, pour lequel nous appliquerons la propriété distributive du produit par rapport à la somme:

√ (2-x) .[√3 + √ (2 + x)] / (1 - x) = √ (6-3x) + √ [(2 -x) (2 + x)] / (1 - x)

Dans l'expression précédente, nous reconnaissons le produit du binomial (2-X) pour son conjugué, qui est le produit remarquable égal à la différence de carrés. De cette façon, une expression rationalisée et simplifiée est enfin obtenue:

[√ (6-3x) + √ (4-x²)] / (1 fois)

- Exercice 5

Développez le produit suivant, en utilisant les propriétés du binôme conjugué:

[2e^{(x + 3y)} - 3e^{(x - 3y)}]].[2e^{(x + 3y)} + 3e^{(x - 3y)}]]

Solution

4e^{(2x + 6y)} - 9e^{(2x - 6y)} = 4A^(2x) .pour^{(6 ans)} - 9e^(2x) .pour^(-6y)= [4A^{(6 ans)} - 9e^(-6y)]] .pour^(2x)

Le lecteur attentif aura remarqué le facteur commun qui a été mis en évidence en couleur.

Les références

1. Baldor, un. 1991. Algèbre. Éditorial culturel vénézuélien s.POUR.
2. González J. Exercices binomiaux conjugués. Récupéré de: Academy.Édu.
3. Mathématiques Alex. Produits remarquables. Récupéré de YouTube.com.
4. Math2me. Binômes conjugués / produits notables. Récupéré de YouTube.com.
5. Produits binomiaux conjugués. Récupéré de: LMS.Colbachenlinea.mx.
6. Vital. Binômes conjugués. Récupéré de: youtube.com.