Applications de parabole dans la vie quotidienne

Une simple parabole. Source: Ezéchia, Wikimedia Commons

Le Applications de parabole dans la vie quotidienne Ils sont multiples. Des antennes satellites et radiomatisées pour concentrer les signaux, aux phares de la voiture lors de l'envoi de faisceaux lumineux parallèles.

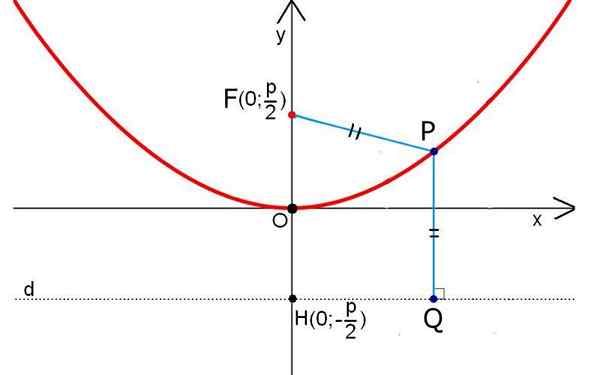
Une parabole, en termes simples, peut être définie comme une courbe dans laquelle les points sont équidistants par rapport à un point fixe et à une ligne. Le point fixe est appelé focus et la ligne est connue sous le nom de directive.

La parabole est une conique qui est dessinée dans différents phénomènes, comme le mouvement d'une balle entraînée par un basketteur ou comme la cascade d'une fontaine.

La parabole est particulièrement importante dans divers domaines de la physique, dans la résistance des matériaux ou en mécanique. À la base de la mécanique et de la physique, les propriétés de la parabole sont utilisées.

Applications de parabole dans la vie quotidienne

Antennes paraboliques

La parabole peut être définie comme une courbe qui surgit lors de la coupe à un cône. Si cette définition s'appliquait à un objet à trois dimensions, nous obtiendrions une surface appelée paraboloïde.

Ce chiffre est très utile en raison d'une propriété que les paraboles ont, où un point à l'intérieur se déplace sur une ligne parallèle à l'axe, "rebondira" dans la parabole et sera envoyé à la focalisation.

Un paraboloïde avec un récepteur de signal à l'orientation peut faire envoyer tous les signaux qui rebondissent dans le paraboloïde au récepteur, sans diriger directement vers le même. Une grande réception de signal est obtenue en utilisant l'ensemble du paraboloïde.

Peut vous servir: les 9 principes de la communication humaine

Ces types d'antennes se caractérisent par un réflecteur parabolique. Sa surface est un paraboloïde de révolution.

Sa forme est due à une propriété de paraboles mathématiques. Ils peuvent être des émetteurs, des récepteurs ou du duplex complet. Ils sont appelés de cette façon lorsqu'ils sont capables de transmettre et de recevoir en même temps. Ils sont généralement utilisés à haute fréquence.

Satellites

Un satellite envoie des informations sur Terre. Ces rayons sont perpendiculaires à la directive pour la distance à laquelle le satellite est situé.

Lorsqu'ils sont reflétés dans le plat d'antenne, qui est généralement blanc, les rayons convergent dans l'orientation, où un récepteur se trouve qui décode l'information.

Jets d'eau

Les jets à eau qui laissent un fournisseur ont une forme parabolique.

Lorsque de nombreux jets d'un point à une vitesse égale sortent, mais avec une inclination différente, une autre parabole appelée "Parabole de sécurité" est au-dessus des autres et il n'est pas possible que toute autre des paraboles restantes sur.

Cuisines solaires

La propriété qui caractérise les paraboles leur permet d'être utilisées pour créer des appareils tels que les cuisines solaires.

Avec un paraboloïde qui reflète les rayons solaires, ce qui va être cuit serait facilement placé, ce qui le rend chaud rapidement.

Les autres utilisations sont l'accumulation d'énergie solaire en utilisant un accumulateur sur la focalisation.

Phares de véhicules et microphones paraboliques

La propriété précédemment expliquée des paraboles peut être utilisée à l'envers. En plaçant un émetteur de signaux situé vers sa surface, tous les signaux rebondiront dans le même. De cette façon, son axe se reflétera en parallèle, obtenant un niveau plus élevé d'émission de signal.

Il peut vous servir: 8 traditions et coutumes de Nayarit

Dans les phares du véhicule, cela a lieu lorsqu'une ampoule est placée pour émettre plus de lumière.

Dans les microphones paraboliques, il se produit lorsqu'un microphone est placé au centre d'un paraboloïde pour émettre une quantité plus sonore.

Ponts suspendus

Les câbles de pont suspendu adoptent la forme parabolique. Ceux-ci forment l'enveloppe d'une parabole.

Dans l'analyse de la courbe d'équilibrage des câbles, il est admis qu'il s'agit de nombreuses sangles et on peut considérer que la charge est distribuée horizontalement uniformément.

Avec cette description, il est démontré que la courbe d'équilibre de chaque câble est une parabole d'équation simple et que son utilisation est fréquente dans la technique.

Comme des exemples de la vie réelle sont le pont de San Francisco (États-Unis) ou le pont Barqueta (Séville), qui utilisent des structures paraboliques pour donner une plus grande stabilité au pont.

Objets célestes

Il existe des comètes périodiques qui ont des trajectoires ou des ellipses allongés. Lorsque le retour effectué par les comètes autour du système solaire n'est pas démontré, ils semblent décrire une parabole.

Des sports

Dans tous les sports dans lesquels un lancement est réalisé, nous trouvons des paraboles. Ceux-ci peuvent être décrits par des balles ou par des artefacts lancés comme le lancement du football, du basket-ball ou du javelot.

Ce lancement est connu sous le nom de "lancement parabolique" et consiste à tirer (pas verticalement) un objet. Le chemin que l'objet fait lors de la hausse (avec la force qui s'applique) et de baisser (par gravité) forme une parabole.

Un exemple plus concret est les pièces faites par Michael Jordan, joueur de basket-ball NBA.

Peut vous servir: que signifie sinaloa?

Ce joueur est devenu célèbre, entre autres, pour ses "vols" vers le panier, où à première vue il semblait être suspendu dans les airs que les autres joueurs.

Le secret de Michael était qu'il savait comment utiliser des mouvements corporels adéquats et une grande vitesse initiale.

Foudre

Lorsqu'un faisceau de forme conique est projeté sur un mur, des formes paraboliques sont obtenues, tant que le mur est parallèle à la génération du cône.

Les références

1. Arnheim, C. (2015). Surfaces mathématiques. Allemagne: corps
2. Boyer, C. (2012). Histoire de la géométrie analytique. États-Unis: Couer Corporation.
3. France, Ronald L. (1980). Une antenne parabolique avec des débordements latéraux très faibles. IEEE fait des transactions sur les antennes et la propagation. 
4. Kletenik, D. (2002). Problèmes de géométrie analytique. Hawaï: le groupe Minerva.
5. Kraus, J.D. (1988). Antennes, États-Unis: McGraw - Hill.