Accélération de la gravité ce qu'elle est, comment elle est mesurée et exerce

La Accélération de la gravité o L'accélération gravitationnelle est définie comme l'intensité du champ gravitationnel terrestre. C'est-à-dire la force que cela exerce sur n'importe quel objet, par unité de masse.

Il est indiqué avec la lettre G déjà familière et sa valeur approximative au voisinage de la surface de la Terre est de 9.8 m / s². Cette valeur peut ressentir de petites variations avec la latitude géographique et également avec la hauteur en ce qui concerne le niveau de la mer.

Astronaute dans le Paseo spatial à la surface de la terre. Source: Pixabay

L'accélération de la gravité, en plus d'avoir l'ampleur mentionnée, a une direction et un sens. En effet, il est dirigé verticalement vers le centre de la terre.

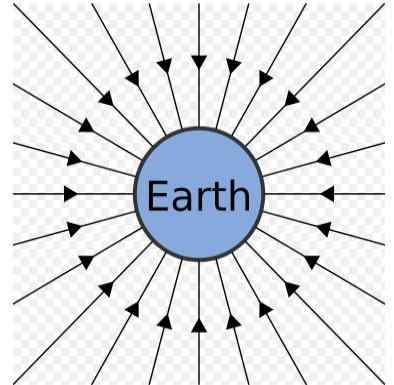Champ gravitationnel de la terre. Source: Source: Sjlegg [Domaine public]

Le champ gravitationnel de la Terre peut être représenté comme un ensemble de lignes radiales qui pointent vers le centre, comme on peut le voir dans la figure précédente.

[TOC]

Quelle est l'accélération de la gravité?

La valeur de l'accélération de la gravité sur la terre ou sur toute autre planète équivaut à l'intensité du champ gravitationnel qu'il produit, qui ne dépend pas des objets qui y sont, mais seulement de sa propre masse et de son rayon.

Souvent, l'accélération de la gravité est souvent définie comme l'accélération ressentie par tout objet en chute libre à proximité de la surface de la Terre.

En pratique, c'est ce qui se passe presque toujours, comme nous le verrons dans les sections suivantes, dans lesquelles la loi universelle de gravitation universelle de Newton sera utilisée.

On dit que Newton a découvert cette célèbre loi tout en méditant à la chute des corps sous un arbre. En ressentant le coup de la pomme dans sa tête, il a immédiatement su que la force qui fait tomber la pomme est la même qui fait l'orbite lune autour de la terre.

La loi universelle sur la gravitation

Une certaine ou non de la légende de la pomme, Newton s'est rendu compte que l'ampleur de la force d'attraction gravitationnelle entre deux objets, par exemple entre la terre et la lune, ou la terre et la pomme, devait dépendre des masses de celles-ci:

Où m₁ Cela peut être la masse de la terre et m_2, La masse de la lune ou de la pomme. Une plus grande masse, une plus grande attraction existe parmi les corps. Mais à plus de distance, moins de force, car cela doit être inversement proportionnel au carré de distance r qui les sépare:

Peut vous servir: chocs élastiques: dans une dimension, des cas spéciaux, des exercices

C'est vrai, quelle que soit la taille des masses en question. En combinant ces faits, la force de la gravité resterait de cette manière:

Une constante de proportionnalité est nécessaire pour préparer cette loi empirique. Newton a calculé la constante G, de sorte que la formule décrit avec toute précision les mouvements des corps célestes à l'échelle du système solaire et au-delà:

Où g = 6.67 x 10^-onze N.m²/kg²

Caractéristiques de la force gravitationnelle

La force gravitationnelle est toujours attrayante; c'est-à-dire que les deux corps auxquels il affecte sont attirés l'un vers l'autre. L'inverse n'est pas possible, car les orbites des corps célestes sont fermées ou ouvertes (comètes, par exemple) et une force de répulsion ne peut jamais produire une orbite fermée. Ensuite, les masses attirent toujours, quoi qu'il arrive.

Une assez bonne approche de la forme réelle de la terre (M₁) Et la lune ou la pomme (m₂) est de supposer qu'ils ont une forme sphérique. La figure suivante est une représentation de ce phénomène.

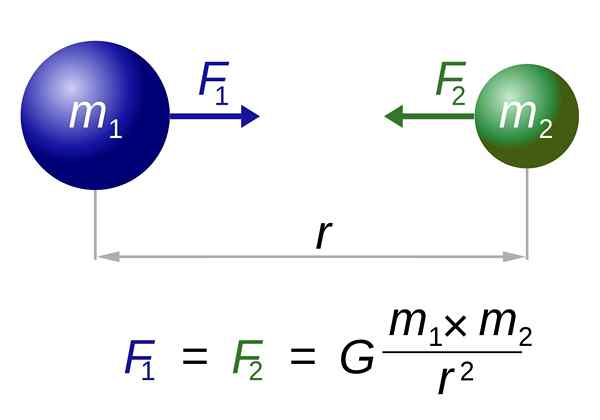Loi de gravitation universelle de Newton. Source: I, Dennis Nilsson [CC par 3.0 (https: // CreativeCommons.Org / licences / par / 3.0)]

Voici les deux la force exercée m₁ À propos de m₂, Comme celui qui exerce m₂ À propos de m₁, à la fois une ampleur égale et dirigée le long de la ligne qui rejoint les centres. Ils ne sont pas annulés, car ils sont appliqués à différents objets.

Dans toutes les sections suivantes, il est supposé que les objets sont homogènes et sphériques, donc son centre de gravité coïncide avec son centre géométrique. Toute la masse concentrée peut être supposée juste là.

Comment la gravité est-elle mesurée sur différentes planètes?

La gravité peut être mesurée avec un limeter, un appareil qui sert à faire du sérieux mesuré dans les enquêtes gravimétriques géophysiques. Ils sont actuellement beaucoup plus sophistiqués que les originaux, mais au début, ils étaient basés sur le pendule.

Le pendule est constitué d'une corde mince, légère et différenciable de longueur L. L'une de ses extrémités est fixée à un support et l'autre pend une masse m.

Lorsque le système est en équilibre, la pâte est suspendue verticalement, mais lorsqu'elle est séparée, elle commence à osciller en cours d'exécution d'un mouvement de swing. La gravité en est responsable. Pour tout ce qui suit, il est valable de supposer que la gravité est la seule force qui agit sur le pendule.

Peut vous servir: ballon aérostatique: histoire, caractéristiques, parties, comment cela fonctionne

La période de swing du pendule pour les petites oscillations est donnée par l'équation suivante:

La force t ne dépend pas de la masse, mais de la longueur du L et de la valeur de g. Les deux membres de l'équation sont carrés:

La relation entre T² et L C'est linéaire: une ligne de la forme y = a.X, où la valeur de pour, La pente de la ligne est précisément (4π²/g).

Expérimenter pour déterminer la valeur de g

Matériaux

- 1 sphérite métallique.

- Corde de plusieurs longueurs différentes, au moins 5.

- Mètre ruban.

- Convoyeur.

- Chronomètre.

- Un support pour définir le pendule.

- MILIMETERING PAPE ou programme informatique avec feuille de calcul.

Procédure

1. Sélectionnez l'une des chaînes et assemblez le pendule. Mesure la longueur de la corde + le rayon de la sphère. Ce sera la longueur L.
2. Retirez le pendule de la position d'équilibre d'environ 5 degrés (Id It avec le transporteur) et laissez-le osciller.
3. Démarrez simultanément le chronomètre et mesurez le temps de 10 oscillations. Notez le résultat.
4. Répétez la procédure précédente pour les autres longueurs.
5. Trouvez le temps qui prend le pendule pour exécuter une oscillation (divisant chacun des résultats précédents par 10).
6. Carré chaque valeur obtenue, obtenant t²
7. Dans le papier millimétrique, graphiquement chaque valeur de t² Sur l'axe vertical, contre la valeur respective de L sur l'axe horizontal. Soyez cohérent avec les unités et n'oubliez pas de prendre en compte l'erreur d'appréciation des instruments utilisés: bande métrique et chronomètre.
8. Tracer la meilleure ligne qui correspond aux points graphiques.
9. Trouver la pente m de cette ligne en utilisant deux points qui lui appartiennent (pas nécessairement des points expérimentaux). Ajouter l'erreur expérimentale.
10. Les étapes ci-dessus peuvent être effectuées avec une feuille de calcul et l'option de construction et de réglage d'une ligne droite.
11. De la valeur de la pente pour effacer la valeur de g Avec leur incertitude expérimentale respective.

Valeur standard de g Sur terre, sur la lune et sur Mars

La valeur standard de la gravité sur terre est: 9.81 m / s², à 45 de la latitude nord et au niveau de la mer. Comme la Terre n'est pas une sphère parfaite, les valeurs de g Ils varient légèrement, étant plus importants dans les poteaux et les mineurs en Équateur.

Ceux qui souhaitent connaître la valeur de leur localité peuvent le trouver mis à jour sur le site Web de l'Institut de métrologie d'Allemagne PTB (Physikalisch-Technische Bundesanstalt), dans la section Système d'information sur la gravité (CRAIE).

Il peut vous servir: Directeur Vector: Équation droite, exercices résolus

La gravité sur la lune

Le champ gravitationnel de la lune a été déterminé par l'analyse des signaux radio de sondes spatiales en orbite autour du satellite. Sa valeur sur la surface lunaire est 1.62 m / s²

La gravité de Mars

La valeur de g_P Pour une planète, cela dépend de sa masse m et de son rayon comme suit:

Donc:

Pour la planète Mars, les données suivantes sont disponibles:

M = 6 4185 x 10²³ kg

R = 3390 km

G = 6.67 x 10^-onze N.m²/kg²

Avec ces données, nous savons que la gravité de Mars est 3.71 m / s². Naturellement, la même équation peut être appliquée aux données de la lune ou à toute autre planète et donc estimer la valeur de sa gravité.

Exercice résolu: la pomme qui tombe

Supposons que la Terre et une pomme aient une forme sphérique. La masse de la terre est m = 5,98 x 10²⁴ kg et son rayon est r = 6,37 x 10⁶  m. La masse de la pomme est m = 0.10 kg. Supposons qu'il n'y ait pas d'autre force que celle de la gravité. De la loi universelle de gravitation de Newton:

a) La force gravitationnelle exercée sur la pomme.

b) l'accélération vécue par la pomme lors de la libération d'une certaine hauteur, selon la deuxième loi de Newton.

Solution

a) La pomme (supposée sphérique, tout comme la terre) a un très petit rayon par rapport au rayon terrestre et est immergé dans son champ gravitationnel. La figure suivante n'est pas évidemment, mais il existe un schéma du champ gravitationnel g, Et le strengh F exercé par la Terre sur la pomme:

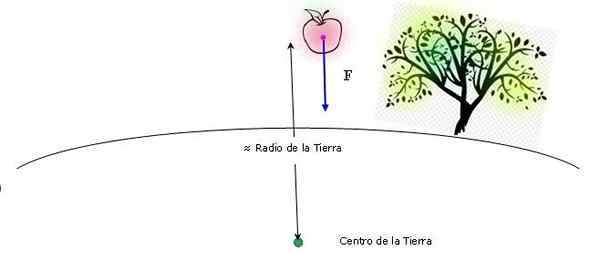Schéma qui montre la chute de la pomme à proximité de la terre. La taille de la pomme et la hauteur de la chute sont méprisables. Source: auto-faite.

Lors de l'application de la loi universelle de gravitation universelle, la distance entre les centres peut être considérée comme approximativement la même valeur que le rayon de la terre (la hauteur à partir de laquelle la pomme tombe est également négligeable par rapport au rayon terrestre). Donc:

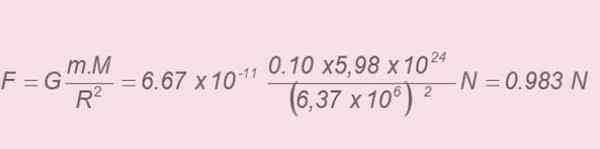
b) Selon la deuxième loi de Newton, l'ampleur de la force exercée sur la pomme est:

F = ma = mg

Dont la valeur est 0.983 n, selon le calcul précédent. L'égalisation des deux valeurs, puis le nettoyage de l'ampleur de l'accélération est obtenu:

mg = 0.983 n

G = 0.983 n / 0.10 kg = 9.83 m / s²

C'est une très bonne approche de la valeur standard de la gravité.

Les références

1. Giancoli, D. (2006). Physique: principes avec applications. Sixième édition. Prentice Hall. 118-122.
2. Hewitt, Paul. (2012). Sciences physiques conceptuelles. CINQUIÈME ÉDITION. Pearson. 91 - 94.
3. Rex, un. (2011). Fondamentaux de la physique. Pearson. 213-221.