Définition de l'accélération centripète, formules, calcul, exercices

La accélération centripète pour_c, Également appelé radial ou normal, c'est l'accélération qui porte un objet mobile lors de la description d'une trajectoire circulaire. Son ampleur est V²/ r, où r C'est le rayon du cercle, il est dirigé vers le centre et est responsable du mobile pour rester dans son itinéraire.

Les dimensions de l'accélération centripète sont de longueur par unité de temps. Dans le système international, ils sont m / s². Si pour une raison quelconque, l'accélération centripète disparaît, la force qui oblige le mobile à maintenir la trajectoire circulaire.

Les objets tournants ont une accélération centripète, qui est dirigée vers le centre de la trajectoire. Source: Pixabay

C'est ce qui arrive à une voiture qui essaie de donner une courbe sur une piste plate et de gel, dans laquelle le frottement entre le sol et les roues est insuffisant pour que la voiture prenne la courbe. Par conséquent, la seule possibilité qu'il vous reste est de se déplacer en ligne droite et c'est pourquoi vous sortez de la courbe.

[TOC]

Mouvements circulaires

Lorsqu'un objet se déplace en cercle, à tout moment, l'accélération centripète est radialement dirigée vers le centre de la circonférence, la direction qui est perpendiculaire à la trajectoire suivie.

Comme la vitesse est toujours tangente à la trajectoire, la vitesse et l'accélération centripète se révèlent perpendiculaires. Par conséquent, la vitesse et l'accélération n'ont pas toujours la même direction.

Dans ces circonstances, le mobile a la possibilité de décrire la circonférence avec une vitesse constante ou variable. Le premier cas est connu sous le nom de mouvement circulaire uniforme ou MCU par son acronyme, le deuxième cas sera un mouvement circulaire variable.

Il peut vous servir: quelle est l'essuyage des émissions? (Avec des exemples)

Dans les deux cas, l'accélération centripète est responsable du maintien du rondage mobile, occupant que la vitesse ne varie que dans la direction et la direction.

Cependant, pour avoir un mouvement circulaire variable, une autre composante d'accélération dans le même sens de la vitesse serait nécessaire, ce qui est responsable de l'augmentation ou de la diminution de la vitesse. Ce composant d'accélération est connu sous le nom Accélération tangentielle.

Le mouvement circulaire variable et le mouvement curviligne en général ont les deux composants de l'accélération, car le mouvement curviligne peut imaginer comme l'itinéraire à travers d'innombrables arcs de circonférence qui composent la trajectoire courbe.

La force centripète

Maintenant, une force est responsable de l'accélération. Pour un satellite qui orbite la terre, c'est la force de la gravité. Et puisque la gravité agit toujours perpendiculairement à la trajectoire, elle ne modifie pas la vitesse du satellite.

Dans ce cas, la gravité agit comme un force centripète, que ce n'est pas une classe spéciale ou en dehors de la force, mais que dans le cas du satellite, est radialement dirigée vers le centre de la terre.

Dans d'autres types de mouvements circulaires, par exemple une voiture qui prend une courbe, le rôle de la force centripète est interprété par une force statique RUBB qui oblige le mobile à tourner.

Formules pour l'accélération centripète

L'accélération centripète est calculée par l'expression:

Ac = V²/ r

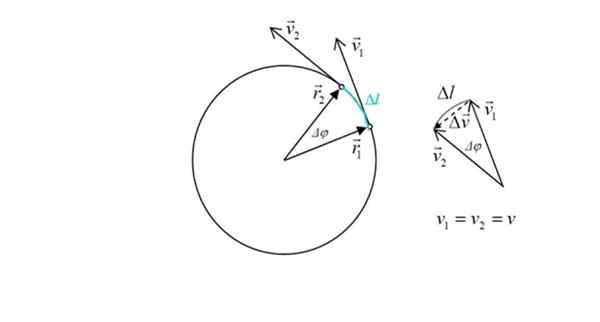Diagramme pour calculer l'accélération centripète dans un mobile avec MCU. Source: Source: Ilevanat [CC BY-SA 3.0 (https: // CreativeCommons.Org / licences / by-sa / 3.0)]

Cette expression sera déduite ci-dessous. Par définition, l'accélération est la variation de la vitesse dans le temps:

Il peut vous servir: sources lumineuses: types et appareils qui émettent de la lumière

Le diagramme supérieur montre dans la figure de gauche, deux points à travers lesquels un mobile passe qui se déplace sur un cercle radio r au sens antihorarium. Notez que l'ampleur de la vitesse est la même dans les deux cas, mais pas dans la direction ou le sens.

Le mobile utilise du temps Δt Sur la tournée, qui est petite, car les points sont très proches.

La figure montre également deux vecteurs de position r₁ et r₂, dont le module est le même: la radio r de la circonférence. L'angle entre les deux points est Δφ. En vert le arc Visite du mobile, indiqué Δl.

Dans la figure à droite, on voit que l'ampleur de δV, Le changement de vitesse est approximativement proportionnel à Δl, car l'angle Δφ est petit. Mais le changement de vitesse est lié précisément à l'accélération. Le triangle est averti, par une somme de vecteurs qui:

V₁ + ΔV = V₂ → ΔV = V₂ - V₁

ΔV C'est intéressant, car il est proportionnel à l'accélération centripète. D'après la figure, il est averti que étant un petit angle Δφ, vecteur δV C'est dans l'essence perpendiculaire V₁ comme V₂ et pointe vers le centre de la circonférence.

Bien que les vecteurs se démarquent en gras, pour les effets de la nature géométrique qui suivent, nous travaillons avec les modules ou les amplitudes de ces vecteurs, quelle que soit la notation vectorielle.

Autre chose: vous devez utiliser la définition de l'angle central, qui est:

Δφ= Δg / D

Maintenant, les deux chiffres sont comparés, qui sont proportionnels depuis l'angle δφ il est courant:

Peut vous servir: qu'est-ce que la lumière polarisée?

 

Diviser entre Δt:

 Puisque par la définition de la vitesse est v = Δl / Δt. Mais ΔV / Δt C'est précisément l'ampleur de l'accélération centripète, qui est ce qui est recherché. De cette façon, l'expression décrite au début est atteinte:

pour_c= V²/ r

Exercice résolu

Une particule se déplace dans un cercle de 2.Radio 70 m. À un certain moment, son accélération est 1.05 m / s² Dans une direction qui fait un angle de 32.0º avec la direction du mouvement. Calculez votre vitesse:

a) À ce moment-là

b) 2.00 secondes plus tard, en supposant une accélération tangentielle constante.

Répondre

Il s'agit d'un mouvement circulaire varié, car l'instruction indique que l'accélération a un angle donné avec la direction du mouvement qui n'est pas ou 0º (ce ne pourrait pas être un mouvement circulaire) ou 90º (ce serait un mouvement circulaire uniforme).

Par conséquent, les deux composants - radiale et tangentiel - coexiste. Sera désigné comme_c déjà_t et sembler dessiné dans la figure suivante. Le vecteur vert est le vecteur d'accélération net ou simplement l'accélération pour.

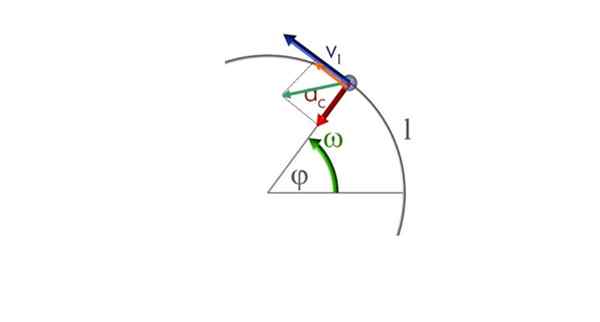Une particule se déplace dans une trajectoire circulaire dans un sens antihoraire et un mouvement circulaire varié. Source: Communes.Wikimedia.org

a) Calcul des composants d'accélération

pour_c = A.cos θ = 1.05 m / s² . cos 32.0º = 0.89 m / s² (en rouge)

pour_t = A.sin θ = 1.05 m / s² . Sen 32.0º = 0.57 m / s² (en orange)

Calcul de la vitesse mobile

Depuis un_c = V²/ r, ensuite:
b) 2 secondes plus tard la vitesse V sera augmenté grâce à la composante tangentielle de l'accélération

V = V_soit +pour_t. T = 1.6 m / s + (0.57 x 2) m / s = 2.74 m / s

Les références

1. Giancoli, D. La physique. 2006. Principes avec les applications. Sixième édition. Prentice Hall. 107-108.
2. Hewitt, Paul. 2012. Sciences physiques conceptuelles. CINQUIÈME ÉDITION.Pearson.106 - 108.