17 problèmes raisonnés

Les Problèmes raisonnés Ils nous aident à résoudre des situations qui peuvent être tous les jours; Par exemple, lorsque plusieurs articles sont achetés et que leur valeur doit être ajoutée pour déterminer le total à payer. L'utilisation du raisonnement logique peut être résolu ces problèmes.

Les problèmes raisonnés, de soustraction ou de multiplication seront d'une importance vitale afin que nous puissions résoudre différentes situations qui se produisent quotidiennement dans les activités de la vie quotidienne.

Vous trouverez ci-dessous une liste de raisons, de soustraction, de multiplication, de division et de fractions. Vous avez d'abord les problèmes et à la fin de cette page les solutions.

Problèmes raisonnés

Problème 1

Problème 2

• Ana, María et Pablo ont décidé de collecter des jouets pour les donner à une fondation. Maria a obtenu 37, Pablo 18 et Ana 26. Combien de jouets ont réussi à élever ensemble?

Problème 3

• Joaquín a une entreprise de crème glacée et doit livrer 3 commandes à différents clients. La première commande est de 650 glaces au chocolat, la deuxième glace à la vanille et la troisième de la crème glacée de 430 fraises. Combien de glaces Joaquín doivent préparer à vos clients?

Problème 4

• Lucia voulait faire un gâteau pour ses amis, alors elle a décidé d'aller au supermarché pour acheter les produits dont elle avait besoin: 1 kg de sucre (2 $), 1 kg de farine de blé (3 $), 1 litre de lait ($ 1), 12 œufs (4 $), 250 gr de beurre (1 $), 250 $ de cerises (4 $) et 250 GR de chocolat (2 $). Combien d'argent Lucia a-t-il dépensé pour l'achat des produits?

Problème 5

• Diego vend un pantalon à différents magasins de la ville et chacun a une valeur de 120 $. Il a distribué 55 pantalons pour le magasin central, 130 pour le magasin de M. Juan et 15 pour le magasin de Luis. Combien de pantalons Diego a-t-il vendu?

Problème 6

• Gabriel voulait acheter une planche à roulettes, mais il n'avait économisé que 50 $. Sa famille voulait l'aider avec l'argent qui lui manquait pour l'acheter: la grand-mère lui a donné 25 $, oncle Miguel 15 $, grand-père Pedro 20 $ et sa tante 15 $. Quelle est la valeur de la planche à roulettes que Gabriel voulait acheter?

Problème 7

• Leonora et Antonio ont quitté la pêche au lac et à la fin de l'après-midi, Leonora a attrapé 28 poissons et Antonio 15. Combien de poissons Leonora a capturé plus qu'Antonio?

Problème 8

• 244 personnes voyageaient dans un train et lorsqu'ils sont arrivés à la gare, 91 personnes ont atterri, tandis que 46 sont montés au train. Combien de personnes voyagent maintenant dans le train, après le départ de la station?

Problème 9

• Ricardo a deux fois plus d'argent que Daniel et entre les deux sont 6 euros. Combien d'argent ont-ils chacun?

Problème 10

• La famille Martínez, 4 membres, achète une boîte avec 60 chocolats au chocolat, chaque personne mange 7 chocolats chacun et garde le reste pour le lendemain. Combien de chocolats étaient?

Problème 11

• La famille Martínez, de 4 membres, distribuera le chocolat au chocolat qui est resté de la veille, de sorte que chacun touche la même quantité. Combien de chocolats peuvent chacun manger?

Problème 12

• Isabel visite la pâtisserie et achète une douzaine de bonbons payant un total de 42 pesos. Le lendemain, le prix de chaque sucré a augmenté de 0.5 pesos chacun. Combien d'argent Isabel a été économisé en les achetant la veille de la hausse du prix?

Problème 13

• Dans une ferme, il y a 12 vaches, deux fois plus que les vaches, les poulets triples que les vaches et aussi 15 chèvres. Quel est le total des animaux à la ferme?

Problème 14

• Un fabricant de meubles bien connu cinquante mille six cent seize armoires pour l'exportation vers 8 pays. Il est connu que chaque pays reçoit le même nombre d'armoires. Combien d'armoires chaque pays a-t-il importé?

Problème 15

Ana se rend sur le marché pour acheter les ingrédients pour préparer une pizza napolitaine:

• 1 ½ kilo de farine

• ¾ kilo de fromage mozzarella

• 1 kilo de tomates

• ½ kilo d'oignons

• ¼ kilo d'anchois

Combien pèse le contenu du sac à provisions?

Problème 16

• Quatre élèves: María, Luis, Raquel et Fernando se rencontrent dans la cafétéria de l'école pour discuter et chacun demande un verre différent. Il y a quatre indices:

i) Qui s'est assis sur la main droite de Luis a demandé au jus d'orange.
ii) María était devant qui je buvais du café.
iii) La gauche de Fernando avait quelqu'un qui buvait cool.
Iv) L'étudiant qui a demandé du thé était assis devant celui qui a bu cool.

Quelle était la boisson de tout le monde?

Problème 17

• Obtenez la bonne fraction:

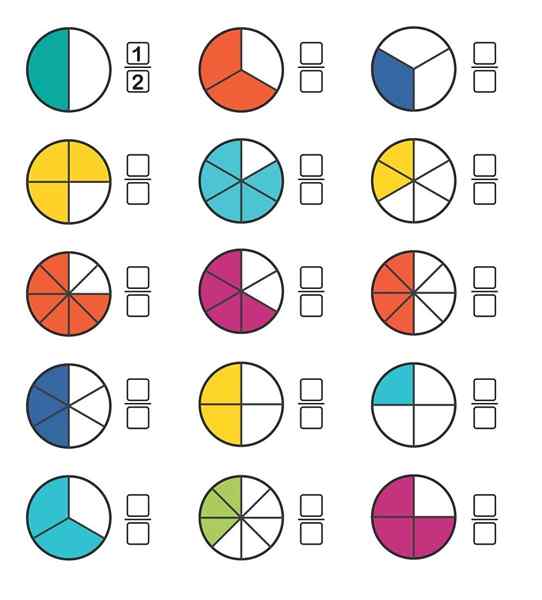
Solutions

Solution au problème 1

• Gallina: 5.
• Canard: 7.
• Porc: 12.

Peut vous servir: Symétrie centrale: propriétés, exemples et exercices

Solution au problème 2

Pour commencer à résoudre, le problème doit d'abord être analysé: il est connu que vous souhaitez obtenir le nombre total de jouets que les trois personnes ont réussi à collecter; c'est-à-dire la somme des jouets collectés par chacun d'eux (Ana, María et Pablo).

Ainsi, le calcul de la somme est fait: 26 + 37 + 17 = 80. Ainsi, il est possible de savoir qu'Ana, María et Pablo ont soulevé 80 jouets entre les trois.

Solution au problème 3

Le nombre total de glaces que Joaquín doit faire pour livrer à ses clients doit être déterminée, sachant qu'il a 3 commandes. En leur ajoutant le montant total est obtenu:

650 + 120 + 430 = 1200 glaces.

Au total, Joaquín a fabriqué 1200 glaces pour livrer à ses 3 clients.

Solution au problème 4

En ajoutant la valeur de chaque produit, le montant d'argent dépensé que Lucia a dépensé dans le supermarché est obtenu:

2 + 3 + 1 + 4 + 1 + 4 + 2 = 17 $.

Lucía a dépensé 17 $ lors de l'achat de produits dans le supermarché.

Solution au problème 5

Ajout du numéro Diego distribué dans chaque magasin le total. Donc, vous avez le pantalon total vendu: 55 + 130 + 15 = 200.

Solution au problème 6

Sachant que Gabriel avait économisé 50 $ et que sa famille lui a donné l'argent qui manquait pour l'acheter, vous pouvez déterminer la valeur du skateboard ajoutant de l'argent de Gabriel plus l'argent que sa famille lui a donné:

50 + 25 + 15 + 20 + 15 = 125 $

La valeur de la planche à roulettes que Gabriel voulait acheter est de 125 $.

Solution au problème 7

La différence dans la quantité de poisson de chacun est:

Peut vous servir: Équations de première dedexes: formule, comment les résoudre, exemple, exercices

28 - 15 = 13 poissons

Par conséquent, Leonora a capturé 13 poissons plus qu'Antonio.

Solution au problème 8

Si 244 personnes voyageaient et ont fixé 91 lorsqu'ils sont arrivés à la gare, ils sont restés dans le train:

244 - 91 = 153 passagers

À ce montant, vous devez ajouter les 46 passagers qui ont augmenté à la gare:

153 + 46 = 199 passagers.

Le train compte 199 passagers en quittant la gare.

Solution au problème 9

Être "x" le montant d'argent que Daniel a et on sait que Ricardo a le double, donc Ricardo a "2x". Entre eux, ils ont 6 euros, ce qui signifie que la somme de x et 2x est égale à 6:

2x + x = 6

Comme "x" et "2x" sont des montants similaires, additionnez pour donner 3x = 6 euros.

Le nombre multiplié par 3 est 6 est 2, donc x = 2.

Daniel est 2 euros et Ricardo, qui a le double, est 4 euros.

Solution au problème 10

Si chaque personne mangeait 7 chocolats chacune et qu'il y avait 4 personnes, le nombre total de chocolats consommés était:

7 × 4 = 28 chocolats

Alors que 60 chocolats sont venus dans la boîte, vous devez soustraire cette quantité des 28 chocolats qui ont été mangés:

60 - 28 = 32 chocolats.

Pour le lendemain, il y a 32 chocolats.

Solution au problème 11

Du problème précédent, il est connu que 32 chocolats ont été laissés le lendemain. Comme ce montant va être réparti également parmi les 4 personnes, 32 doivent être divisés par 4:

32 ÷ 4 = 8

Chaque membre de la famille correspond à 8 chocolats.

Solution au problème 12

Il est d'abord nécessaire de découvrir le prix (en pesos) de chaque sucré. Le jour où Isabel a visité la pâte, pour cela, l'argent total dépensé (42 pesos) est divisé par la quantité de bonbons achetés (1 douzaine = 12 bonbons):

42 ÷ 12 = 3.5 pesos

Chaque coût doux 3.5 pesos le jour Isabel les a achetés, mais le lendemain, le prix de chaque sucré est:

3.5 + 0.5 = 4.0 pesos

Si Isabel avait acheté une douzaine de bonbons à 4 pesos chacun, elle aurait dû payer un total de:

4 × 12 = 48 pesos

Par conséquent, Isabel a économisé la différence entre le nouveau prix et le prix précédent:

Économies = 48 pesos - 42 pesos = 6 pesos.

Solution au problème 13

Pour commencer, il est connu qu'il y a 12 vaches, il peut donc être établi que:

Nombre de vaches = 12

S'il y a deux fois plus que les vaches, alors:

Quantité de porcs = 2 × 12 = 24

Ensuite, la déclaration indique qu'il y a des poulets triples que les vaches et puisque il y a 12 vaches:

Nombre de poulets = 3 × 12 = 36

Enfin, on sait qu'il y a 15 chèvres:

Peut vous servir: quelles sont les parties de l'avion cartésien?

Quantité de chèvres = 15

Le nombre total d'animaux habitant la ferme ajoute tous les résultats:

Animaux totaux = 12 vaches + 24 cochons + 36 poulets + 15 chèvres = 87 animaux.

La réponse est: il y a 87 animaux à la ferme.

Solution au problème 14

Comme chaque pays importe le même nombre d'armoires, le total est divisé par le nombre de pays:

56616 ÷ 8 = 7077 armoires.

La réponse est: chaque pays a importé 7077 armoires.

Solution au problème 15

Pour connaître le poids total, vous devez ajouter le poids de chaque ingrédient. Notez que le poids de la farine est sous la forme d'un nombre mixte, car il a une partie entière: 1 kilo, plus une partie fractionnaire ½. Avant d'ajouter le poids de la farine avec celui des autres ingrédients, le nombre mixte doit être exprimé comme une fraction incorrecte:

Cela fait, la somme de tous les ingrédients de la pizza peut déjà être soulevée, en tenant compte du fait que 1 kilo de tomate peut également être exprimé comme une fraction:

Sac d'achat d'ANA 4 kg.

Solution au problème 16

Ce problème peut être résolu en créant un schéma qui représente les informations offertes par la déclaration. Une suggestion consiste à couper quatre cartes avec les noms des étudiants et les figures des quatre boissons, les mettant sur une table, pour organiser les informations peu par petit.

Avec la table et les convives vus d'en haut, il commence par Luis, que sur sa main droite, il avait un jus d'orange. C'est sûr que Luis n'a pas bu du jus d'orange.

Figure suggérée pour organiser des informations dans le problème des quatre convives et de leurs boissons. Source: F. Zapata.

Ensuite, il est indiqué que Maria était assise devant qui elle a bu du café, donc il y a deux possibilités: 1) Maria a pris du jus d'orange ou 2) elle s'est assise devant Luis, qui a bu du café. Ce qui est sûr pour l'instant, c'est que Maria n'a pas bu du café.

Il n'est pas encore possible de décider de la bonne option, donc les informations suivantes sont examinées: "La gauche de Fernando avait quelqu'un à boire du soda de queue". Puis Fernando n'a pas pris de soda frais.

Ensuite, vous devez "qui a demandé que le thé était assis devant ceux qui buvaient de la bobine". Ce ne peut pas être Fernando, car qui a pris du soda frais était sur sa main gauche. Luis ne s'est pas assis devant Fernando. Puis Fernando a demandé 1) le café ou 2) le jus d'orange et l'étudiant qui a demandé le thé devait 1) être Luis ou 2) être devant Luis.

Mais la personne qui a pris du cola soda est à gauche de Fernando, alors Luis est celui qui a bu le thé et puisque Maria n'a pas bu du café, c'était la boisson de Fernando:

À ce stade, il a déjà été déduit que la boisson de Luis est le thé et que Fernando est Café. Source: F. Zapata.

Alors que Maria était assise devant ceux qui buvaient du café, c'est elle qui a pris du jus d'orange et par défausse, Raquel a bu du soda de la queue. Le puzzle est comme ceci:

Ainsi, les quatre convives et leurs boissons respectives étaient assis. Le lecteur peut-il suggérer une autre façon de résoudre l'énigme? Source: F. Zapata.

Solution au problème 17

1. ¹⁄2
2. ²⁄3
3. ¹⁄3
4. ³⁄4
5. ⁵⁄₆
6. ²⁄₆
7. ⁶⁄8
8. ⁴⁄₆
9. ⁴⁄8
10. ³⁄₆
11. ²⁄4
12. ¹⁄4
13. ²⁄4
14. ³⁄8
15. ³⁄4