X carré

Nous expliquons ce qui est x au carré, ses propriétés, ses exemples et ses exercices résolus

La zone d'un carré de «x» est x carré. Source: F. Zapata.

L'opération algébrique de "X carré"Il est effectué en multipliant le montant" x "avec lui-même deux fois. Cela fait partie des opérations de potentialisation, et dans les symboles mathématiques, il s'exprime de cette manière:

x ∙ x = x²

Il s'agit d'un cas particulier d'autonomisation, dans lequel "x" représente le base Et le "2" est le exposant. Si dans une opération, le terme x apparaît², Il se lit précisément comme "x carré" ou "x carré surélevé".

Naturellement, d'autres exposants sont possibles, par exemple, si l'exposant est 3, alors la puissance est écrite comme suit:

x ∙ x ∙ x = x³

Et lisez comme "x aux trois", "x levé sur le cube" ou simplement "x au cube".

En général, l'exposant auquel la base est élevée peut être n'importe quel nombre, appelé "n" et dans ce cas, la puissance correspondante est écrite:

Xⁿ = x ∙ x ∙ x ∙… ∙ x

Ici, les points suspendus indiquent que «x» doit être multiplié par lui-même «n», c'est-à-dire autant de fois que l'exposant l'indique.

Quelques exemples simples de "x carré", avec des chiffres, sont les suivants:

3² = 3 ∙ 3 = 9

(−4)² = (−4) ∙ (−4) = 16

Plus tard, diverses applications sont décrites pour lesquelles il est nécessaire.

Propriétés de potentialisation

En général, le produit de toute quantité avec lui-même, n fois, elle est appelée potentialisation. Le calcul de X carré n'est qu'un cas particulier de potentialisation, deux autres cas apparaissent lorsque vous souhaitez augmenter un montant à l'exposant 1, obtenant en conséquence le même montant:

Peut vous servir: lois des exposants

Comme ces opérations sont fréquentes, pour travailler avec des bases et des exposants, certaines règles de fonctionnement simples sont suivies, appelées Lois des exposants, qui sont répertoriés ci-dessous:

Lois des exposants

Dans ce qui suit, "x" est la base et "n" et "m" sont les exposants.

1.- Produit de pouvoirs de base égaux

En multipliant deux (ou plus) pouvoirs de base égale, la base élevée à la somme des exposants est obtenue:

Xⁿ∙ x^m = x^{n + m}

Dans le cas de X High, cette règle est appliquée comme suit, remplaçant N et M pour 1:

X¹∙ x¹ = x^{1 + 1} = x²

2.- Division des pouvoirs de base égale

En divisant les pouvoirs de la même base, la base est obtenue, soulevée à la soustraction entre les exposants respectifs du numérateur et du dénominateur:

Xⁿ ÷ x^m = x^N-m

Comme la division par 0 n'est pas définie, elle doit être remplie à condition que x ≠ 0.

3.- Pouvoir d'une puissance

Le résultat de la puissance d'une puissance est égal à la base élevée au produit des exposants:

(X^m)ⁿ = x^m∙n

Il peut être obtenu à nouveau x carré, lorsqu'il fait m = 1 et n = 2:

(X¹)² = x^1∙2 = x²

4.- Exposant négatif

Pour les exposants négatifs, l'opération à effectuer est:

Chaque fois que x ≠ 0. Notez que, dans ce cas, la puissance devient une fraction avec un numérateur égal à 1.

5.- Exposant fractionnaire

Les exposants fractionnaires peuvent être écrits comme la nième racine de la base:

À condition que n est différent de 0. Cette valeur devient l'indice de racine, tandis que m devient l'exposant de la quantité sous la racine, qui dans ce cas est x.

Peut vous servir: quelle est la directive? (Géométrie)

Produits et quotients de différentes bases

Lorsque vous devez améliorer les produits et les quotients de différentes bases "x" et "y", ces règles sont suivies:

1.- Puissance du produit

Pour effectuer cette puissance, chaque montant est collecté à l'exposant N et le produit résultant est établi:

(x ∙ y)ⁿ = xⁿ ⋅ etⁿ

2.- Rapport du quotient

Encore une fois, chaque montant doit être soulevé à l'exposant n séparément et établir le quotient qui en résulte, en suivant la règle selon laquelle le montant «y» est différent de 0, dans le cas de «N» positif:

(x ÷ y)ⁿ = xⁿ ÷ Yⁿ

Lorsque "n" est négatif, il faut faire preuve de prudence, en raison de la propriété 4 de la section précédente, le numérateur devient un dénominateur. Dans ce cas, les deux montants doivent être différents de 0, car la division de 0 doit être évitée à tout prix.

Exemples

Exemple 1: Places de nombres naturels

Les carrés des dix premiers numéros naturels sont:

• 1²= 1 × 1 = 1
• 2²= 2 × 2 = 4
• 3²= 3 × 3 = 9
• 4²= 4 × 4 = 16
• 5²= 5 × 5 = 25
• 6²= 6 × 6 = 36
• 7²= 7 × 7 = 49
• 8²= 8 × 8 = 64
• 9²= 9 × 9 = 81
• dix²= 10 × 10 = 100

Exemple 2: le carré des nombres négatifs

Le carré d'un nombre négatif est toujours positif, car deux quantités de signe égal sont donc multipliées:

(-x) · (-x) = x ∙ x = x²

Par exemple:

(-2) · (-2) = (-2)² = 4

Exemple 3: carré de la somme et de la différence

Il est souvent nécessaire de calculer le carré de la somme de deux quantités, ou sa différence, des opérations qui sont incluses dans la catégorie des produits notables.

L'opération est résolue avec les indications données et l'aide de la propriété distributive:

Carré de la somme

Laissez deux quantités "x" et "y", et vous voulez trouver le carré de sa somme (x + y)²:

Peut vous servir: hiérarchie des opérations

(x + y)² = (x + y) ∙ (x + y) = x ∙ x + x ∙ y + y ∙ x + y ∙ y = x² + 2x ∙ y + et²

Cette expression se lit comme suit: "carré du premier, plus le double produit du premier pour le second plus le carré du second".

Carré de différence

Il est résolu de manière analogue, mais en tenant compte du signe négatif:

(x - y)² = (x - y) ∙ (x - y) = x ∙ x - x ∙ y + y ∙ x - y ∙ y = x² - 2x ∙ et + et²

Exemple 4: la zone d'un carré

Le carré est un polygone à 4 faces, qui a la même mesure. Soit ℓ la mesure latérale, alors la zone A de la figure est donnée par:

A = ℓ²

Exemple 5: Théorème de Pythagore

Ce théorème s'applique aux triangles rectangulaires, ceux sur lesquels deux de ses côtés forment un angle droit. Ces côtés sont appelés "catégories" et le côté restant est "l'hypoténuse".

Le théorème établit que le carré de l'hypotenusa est égal à la somme des carrés des catégories. Appelant "A" et "B" aux catégories, et "C" à l'hypoténuse, le théorème est écrit comme:

c² = A² + b²

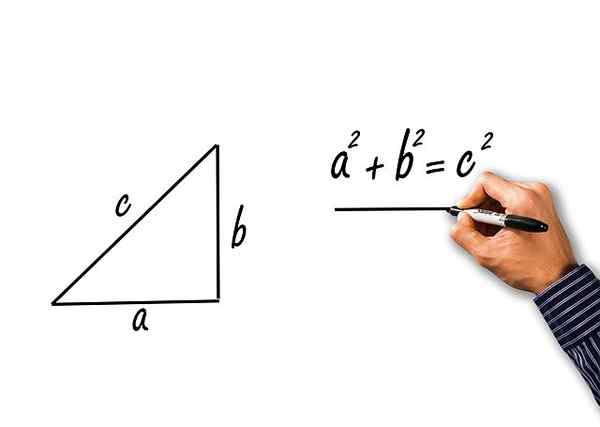Théorème de Pythagore pour un triangle rectangle de chats A et B, et Hypotenusa C

Exercices résolus

Exercice 1

Calculez le carré de l'hypoténuse dont les jambes mesurent 3 et 5 unités.

Solution

Selon le théorème de Pythagore, le carré de l'hypoténuse est:

c² = A² + b²

Remplacement des valeurs:

c² = 3² + 5²= (3 × 3) + (5 × 5) = 9 + 25 = 34

Exercice 2

Déterminez l'aire d'un carré latéral ℓ = 6 cm

Solution

A = ℓ² = (6 cm)² = 36 cm²