Vecteurs d'unité caractéristiques, comment le sortir, exemples

Les vecteurs unitaires sont ceux dont le module, l'amplitude ou la taille sont égaux à la valeur numérique. Les vecteurs unitaires sont utiles pour indiquer la direction d'autres vecteurs non unit.

Rappelons que les vecteurs sont des entités mathématiques qui représentent mathématiquement les amplitudes physiques qui dépendent de la direction, telles que la force, la vitesse, l'accélération et d'autres.

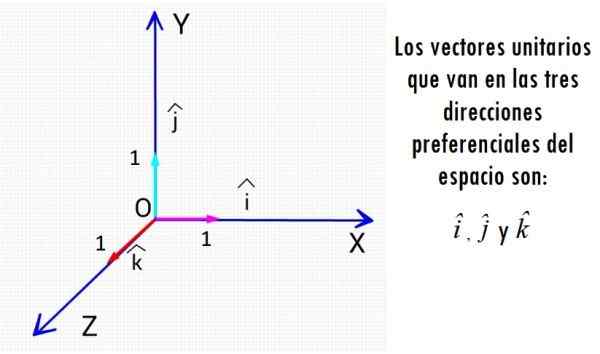
Les vecteurs unitaires les plus connus sont les trois vecteurs qui vont dans les directions des axes cartésiens. Source: F. Zapata.

Quelle que soit la magnitude physique associée, les vecteurs unitaires sont des entités manquant d'unités de mesure et leur taille est toujours 1, un nombre pur.

Par exemple, la vitesse d'une particule qui se déplace à 3 m / s va dans la direction positive de l'axe x cartésien est indiquée: V = (3 m / s) Toi, où la lettre audacieuse est utilisée pour indiquer les montants vectoriels. Dans cet exemple, le module de V Il est de 3 m / s et le module vectoriel unitaire Toi est 1 (sans unités).

[TOC]

Module, direction et signification

Étant donné l'important. Au moment de représenter un montant vectoriel, il est nécessaire d'indiquer clairement ces aspects.

Maintenant, un vecteur unitaire peut avoir n'importe quelle direction et la signification préférée, mais l'ampleur doit toujours être égale à 1.

Les vecteurs unitaires sont utilisés pour indiquer une adresse privée dans l'espace ou dans l'avion. Si, par exemple, nous devons travailler avec toutes les forces qui agissent le long de l'axe horizontal, car un vecteur unitaire dans cette direction nous aide à distinguer ces forces des autres dirigés dans une direction différente.

Et pour les distinguer des vecteurs non unit, le gras est généralement utilisé sur l'impression et placer un accent circonflexe sur le dessus, par exemple:

Il peut vous servir: théorie de l'état stationnaire: histoire, explication, nouvelles

Pour les paroles manuscrites, il suffit de placer le circonflejo pour comprendre qu'il s'agit d'un vecteur d'unité.

Caractéristiques d'un vecteur unitaire

Mathématiquement le vecteur d'unité:

C'est un élément qui appartient à un espace vectoriel ℛ de dimension n, tel que |V| = 1, où les barres signifient "module".

Nous pouvons donc établir cela:

-Le module vectoriel unitaire est toujours 1, peu importe s'il s'agit d'une force, d'une vitesse ou d'un autre vecteur.

-Les vecteurs unitaires ont une certaine direction, ainsi que la direction, comme le vecteur unitaire dans la direction verticale, ce qui peut avoir un sens vers le haut ou vers le bas.

-Les vecteurs unitaires ont un point d'origine. Lorsqu'il est représenté par un système de coordonnées cartésiennes, ledit point coïncide avec l'origine du système: (0,0) si c'est le plan ou (0,0,0) si le vecteur est dans l'espace à trois dimensions.

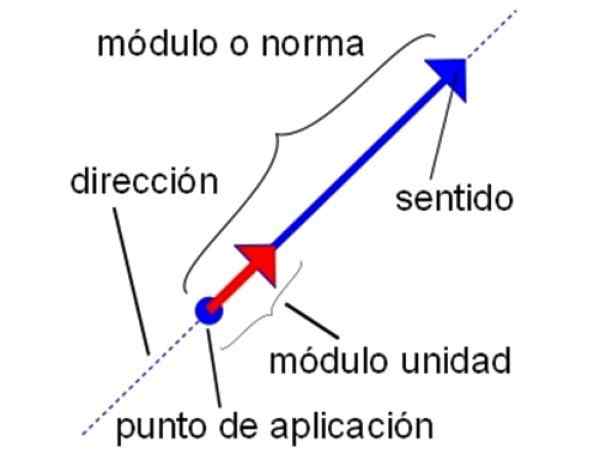Les caractéristiques du vecteur unitaire. Source: Wikimedia Commons.

-Aussi avec les vecteurs unitaires, toutes les opérations de la somme, de la soustraction et de la multiplication vectorielle qui sont fabriquées par des vecteurs réguliers peuvent être effectuées. Par conséquent, il est valable de multiplier le vecteur unitaire par un scalaire, ainsi que pour effectuer le produit ponctuel et le produit croisé.

-Avec un vecteur unitaire dans une certaine direction, d'autres vecteurs peuvent également être exprimés qui sont également orientés dans cette direction.

Les vecteurs unitaires dans l'espace

Pour exprimer tout vecteur dans l'espace ou dans le plan, vous pouvez utiliser un ensemble de vecteurs unitaires perpendiculaires les uns aux autres, qui forment une base ortonormale. Chacune des trois directions préférentielles de l'espace a son propre vecteur unitaire.

Revenons à l'exemple des forces dirigées le long de l'axe horizontal. Ceci est l'axe x, qui a deux possibilités: la direction à droite et la direction vers la gauche. Supposons qu'il y ait un vecteur unitaire sur l'axe x et dirigé vers la droite, que nous pouvons désigner à travers l'une de ces formes:

Peut vous servir: Modèle atomique Thomson: caractéristiques, postulats, particules subatomiques

L'un d'eux est valable. Maintenant, supposons une force F₁ de magnitude 5 N le long de cet axe et dirigé vers la droite, une telle force pourrait être exprimée comme suit:

Si la force était dirigée le long de l'axe x mais dans la direction opposée, c'est-à-dire à gauche, alors un signe négatif pourrait être utilisé pour établir cette différence.

Par exemple, une force de grandeur de 8 n, située sur l'axe x et dirigé vers la gauche serait comme ceci:

Ou du moins:

Et pour les vecteurs qui ne sont pas dirigés le long des axes cartésiens, il existe également un moyen de les représenter en termes de vecteurs d'unité orthogonaux, à travers leurs composants cartésiens.

Comment supprimer / calculer le vecteur d'unité?

Pour calculer le vecteur unitaire dans le sens de tout vecteur arbitraire V, La formule suivante est appliquée:

Où:

C'est le module ou l'ampleur du vecteur V, dont le carré est calculé comme ceci:

|V|² = (V_X)² +  (V_et)²+  (V_z)²

Un vecteur arbitraire en termes de vecteur unitaire

Alternativement le vecteur V Il peut être exprimé comme suit:

C'est-à-dire le produit de son module par le vecteur d'unité correspondant. C'est exactement ce qui a été fait avant, lorsque vous parlez de la force de 5 N de grandeur dirigée le long de l'axe x positif.

Représentation graphique

Graphiquement, ce qui est dit est vu dans cette image, où le vecteur V Il est en bleu et le vecteur unitaire correspondant dans sa direction est en rouge.

Dans cet exemple, le vecteur V Il a une ampleur supérieure à celle du vecteur unitaire, mais l'explication est même valide si cela ne se produit pas. En d'autres termes, nous pouvons avoir des vecteurs qui sont par exemple 0.25 fois le vecteur unitaire.

Peut vous servir: poids (physique): calcul, unités, exemples, exercices

Exemples de vecteurs unitaires

Les vecteurs d'unité perpendiculaire I, J et K

Comme nous l'avons vu auparavant, des vecteurs d'unité perpendiculaire Toi, J et k Ils sont très utiles pour représenter tout autre vecteur dans l'avion ou l'espace et effectuer des opérations vectorielles. En termes de ce vecteur, un vecteur arbitraire V est représenté comme suit:

V = V_X Toi + V_et J + V_z k

Où V_X, V_et et V_z sont les composants rectangulaires du vecteur V, qui sont des montées -bold ne sont pas utilisées pour les représenter dans le texte imprimé-.

La loi de coulomb

Les vecteurs unitaires apparaissent fréquemment en physique. Là, nous avons la loi de Coulomb, par exemple, qui décrit quantitativement l'interaction entre deux charges électriques spécifiques.

Cela indique que la force F d'attraction ou de répulsion entre ces charges est proportionnelle à leur produit, inversement proportionnel au carré de la distance qui les sépare et est dirigée dans le sens du vecteur unitaire qui rejoint les charges.

Ce vecteur est généralement représenté par:

Et la loi de Coulomb est comme ça, sous une forme vectorielle:

Où k C'est la constante électrostatique, q₁ et q₂ Ce sont les charges et r C'est la distance qui les sépare.

Exercice résolu

Trouvez le vecteur unitaire dans le sens du vecteur V = 5Toi + 4J -8k, Donné dans des unités arbitraires.

Solution

La définition du vecteur unitaire ci-dessus est appliquée ci-dessus:

Mais d'abord, vous devez calculer le module vectoriel qui, comme il a trois composants, est déterminé par:

|V|² = (V_X)² +  (V_et)² +  (V_z)²

Rester:

|V|² = (5)² +  (4)² +  (-8)²= 25 + 16 + 64 = 105

Par conséquent, le module de V est:

|V| = √105

Le vecteur unitaire recherché est simplement:

Cela nous amène enfin à:

V = 0.488 Toi + 0.390 J - 0.781 k

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
2. Bedford, 2000. POUR. Mécanique pour l'ingénierie: statique. Addison Wesley.
3. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 1. Cinématique. Édité par Douglas Figueroa (USB).
4. Giambattista, un. 2010. La physique. 2e. Élégant. McGraw Hill.
5. Resnick, r. (1999). Physique. Vol. 1. 3e édition. en espagnol. Société de rédaction continentale S.POUR. de c.V.