Caractéristiques, exemples et exercices des vecteurs simultanés

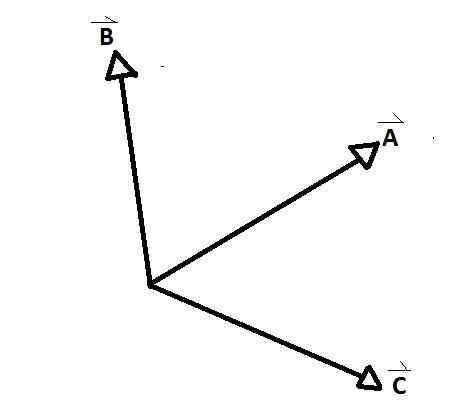
Les vecteurs simultanés Ce sont les groupes de vecteurs dont les axes coïncident à un point, formant entre chaque paire un angle interne et externe. Un exemple clair est observé dans la figure inférieure, où A, B et C sont des vecteurs simultanés les uns avec les autres.

D et E contrairement aux autres ne sont pas. Il y a des angles formés parmi les vecteurs simultanés AB, AC et CB. Les angles de relation entre les vecteurs sont appelés.

[TOC]

Caractéristiques

-Ils ont un point commun, qui coïncide avec leur origine: toutes les amplitudes des vecteurs simultanés commencent d'un point commun à leurs extrêmes respectifs.

-L'origine est considérée comme le point d'action vectoriel: un point d'action doit être établi qui sera directement affecté par chacun des vecteurs simultanés.

-Votre domaine dans l'avion et l'espace est R² et r³ respectivement: les vecteurs simultanés sont libres de couvrir l'ensemble de l'espace géométrique.

-Permet des notations différentes dans le même groupe de vecteurs. Selon les branches d'étude, différentes notations sont présentes dans les opérations avec des vecteurs.

Types de vecteurs

La branche des vecteurs a plusieurs subdivisions, parmi certaines, elles peuvent être nommées: le parallèle, perpendiculaire, coplanarios, correspondant, opposé et unitaire. Les vecteurs simultanés apparaissent sur cette liste et, comme tous ceux qui ont été nommés précédemment, ils ont de nombreuses applications dans différentes sciences.

Ils sont très communs dans l'étude vectorielle, car ils représentent une généralisation rentable dans les opérations avec eux. À la fois dans l'avion et dans l'espace, les vecteurs simultanés sont pour une utilisation actuelle pour la représentation de différents éléments et étudient leur influence sur un système particulier.

Notation vectorielle

Il existe différentes façons de représenter un élément vectoriel. Les principaux et les plus connus sont:

cartésien

Proposé par cette même approche mathématique, désigne des vecteurs avec une liste correspondant aux amplitudes de chaque axe (x, y, z)

A: (1, 1, -1) espace A: (1, 1) plan

Polaire

Ils ne servent qu'à désigner les vecteurs dans le plan, bien que dans le calcul intégral, le composant de profondeur soit attribué. Il consiste avec une ampleur linéaire r et un angle par rapport à l'axe polaire Ɵ.

Peut vous servir: statistiques inférentielles: historique, caractéristiques, à quoi sert, des exemples

R: (3, 45⁰ ) Plan A: (2, 45⁰ , 3) espace

Analytique

Définissez les amplitudes du vecteur à travers les Versors. Les verseurs (R&E + K) représentent les vecteurs unitaires correspondant aux axes X, y et

A: 3i + 2j - 3k

Sphérique

Ils sont similaires à la notation polaire, mais avec l'ajout d'un deuxième angle qui balaie dans le plan Xy symbolisé par δ.

R: (4, 60^soit , π / 4)

Opérations avec des vecteurs simultanés

Les vecteurs simultanés sont principalement utilisés pour définir les opérations entre les vecteurs, car il est plus facile de comparer les éléments des vecteurs lorsqu'ils se produisent de manière simultanée.

Sum (a + b)

La somme des vecteurs simultanés vise à trouver le vecteur résultant V_r. Qui, selon la branche de l'étude, correspond à une action finale

Par exemple: 3 chaînes sont liées a, b, c à une boîte, chaque extrémité de la corde est entre les mains d'un sujet. Chacun des 3 sujets doit tirer la corde dans une direction autre que les 2 autres.

A: (AX, AY, AZ) B: (BX, BY, BZ) C: (CX, CY, CZ)

A + b + c = (ax + bx + cx; ay + by + cy; az + bz + cz) = V_r

La boîte ne peut se déplacer que dans une seule direction, donc V_r indiquera la direction et le sens du déplacement de la boîte.

Différence (a - b)

Il existe de nombreux critères concernant la différence entre les vecteurs, de nombreux auteurs choisissent de l'exclure et affirment que seule la somme entre les vecteurs est stipulée, où la différence est la somme du vecteur opposé. La vérité est que les vecteurs algébriquement peuvent être soustraits.

A: (AX, AY, AZ) B: (bx, par, bz)

A-b = a + (-b) = (ax-bx; ay-be; az-bz) = [ax + (-bx); ay + (-By); az + (-bz)]

Produit scalaire (un . B)

Également connu sous le nom de produit Punto, génère une valeur scalaire qui peut être liée à plusieurs grandeurs selon la branche de l'étude.

Pour la géométrie indique la zone de parallélogramme formée par la paire de vecteurs simultanés à travers la méthode de parallélogramme. Car la physique mécanique définit le travail effectué par une force F En déplaçant un corps à distance Δr.

Il peut vous servir: proportionnalité composée: explication, trois règles composées, exercices

ѡ = f . Δr

Comme son nom l'indique, il génère une valeur scalaire et est défini comme suit:

Être les vecteurs A et B

A: (AX, AY, AZ) B: (bx, par, bz)

-Formulaire analytique:

( POUR . B) = | a |.| B |.Cos θ

Où θ est l'angle interne entre les deux vecteurs

-Forme algébrique:

( POUR . B) = (hache.Bx + ay.par + az.Bz)

Produit vectoriel (a x b)

Le vecteur ou le produit point entre deux vecteurs, définit un troisième vecteur C qui a la qualité d'être perpendiculaire B et C. En physique définit le couple vecteur τ Élément de base de la dynamique de rotation.

-Formulaire analytique:

| A x b | = | A |.| B |.Sin θ

-Forme algébrique:

(A x b) = = (Hache . par - oui . bx) - (hache . Bz - az . bx) J + (Hache . par - oui . bx) k

-Mouvement relatif: R_{Un B}

La base de la relativité est le mouvement relatif et les vecteurs simultanés sont à la base du mouvement relatif. Vous pouvez déduire des positions, des vitesses et des accélérations relatives en appliquant l'ordre des idées suivant.

r _{Un B} = r_POUR - r_B    ; Position relative concernant b

V _{Un B} = V_POUR - V_B  ; Vitesse relative de respect à b

pour _{Un B} = A_POUR - pour_B  ; Accélération relative du respect à B

Exemples: exercices résolus

Exercice 1

Soit A, B et C vecteurs simultanés.

A = (-1, 3, 5) b = (3, 5, -2) c = (-4, -2, 1)

-Définir le vecteur résultant V_r = 2a - 3b + c

2a = (2 (-1), 2 (3), 2 (5)) = (-2, 6, 10)

-3b = (-3 (3), -3 (5), -3 (-2)) = (-9, -15, 6)

V_r = 2a + (-3b) + c = (-2, 6, 10) + (-9, -15, 6) + (-4, -2, 1)

V_r = ([-2 + (- 9) + (- 4)]; [6 + (- 15) + (- 2)]; (10 + 6 + 1))

V_r = (-15, -11, 17)

-Définir le produit scalaire (un . C)

( POUR . C) = (-1, 3, 5) . (-4, -2, 1) = (-1) (-4) + 3 (-2) + 5 (1) = 4 -6 + 5

( POUR . C) = 3

-Calculez l'angle entre A et C

( POUR . C) = | a |.| C |.Cos θ où θ est l'angle le plus court parmi les vecteurs

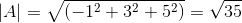
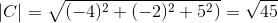
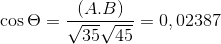
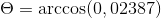
θ = 88,63⁰

 -Trouvez un vecteur perpendiculaire à A et B

Pour cela, il est nécessaire de définir le produit vectoriel entre (-1, 3, 5) et (3, 5, -2). Comme expliqué précédemment, une matrice 3 x 3 est construite où la première ligne est composée de la liste des vecteurs unitaires (i, j, k). Ensuite, la 2e et la 3e rangée est composée des vecteurs à utiliser, en respectant l'ordre opérationnel.

Peut vous servir: notation décimale

(A x b) = = [(-1) . 5 - (3 . 3)] Toi  - [ (-1) . (-2) - (5 . 3)] J + [ (-1) . 5 - (3 . 3)] k

(A x b) = (-5 - 9) Toi - (2 - 15) J + (-5 - 9) k         

(A x b) =  -14 I + 13 J - 14 K

Exercice 2 

Laissez V_pour et V_b Les vecteurs de vitesse de A et B respectivement. Calculez la vitesse b à un.

V_pour = (3, -1, 5) v_b = (2, 5, -3)

Dans ce cas, la vitesse relative de b est demandée à V_{B / a}

V_{B / a} = V_B - V_POUR

V_{B / a} = (2, 5, -3) - (3, -1, 5) = (-1, 6, -8)

C'est le vecteur Veloc de b vu à partir d'un. Où un nouveau vecteur de la vitesse b est décrit par référence d'un observateur positionné en A et se déplaçant avec la vitesse d'un.

Exercices proposés

1-Construct 3 vecteurs A, B et C qui sont simultanés et relient 3 opérations entre eux par un exercice pratique.

2-vecteurs a: (-2, 4, -11), b: (1, -6, 9) et c: (-2, -1, 10). Trouvez des vecteurs perpendiculaires à: a et b, c et b, sum a + b + c.

4-détermine 3 vecteurs perpendiculaires les uns aux autres, sans prendre en compte les axes de coordonnées.

5 définir le travail effectué par une force qui soulève un bloc de masse de 5 kg, du bas d'un puits de 20 mètres de profondeur.

Algébrique 6-méprisant que la soustraction des vecteurs est égale à la somme du vecteur opposé. Justifiez vos postulats.

7-Denote un vecteur dans toutes les notations développées dans cet article. (Cartésien, polaire, analytique et sphérique).

8-Les forces magnétiques exercées sur un aimant qui repose sur une table, est donnée par les vecteurs suivants; V: (5, 3, -2), t: (4, 7, 9), h: (-3, 5, -4). Déterminer dans quelle direction l'aimant se déplacera si toutes les forces magnétiques agissent en même temps.

Les références

1. Géométrie et transformations euclidiennes. Clayton W. Esquiver. Couer Corporation, 1 janvier. 2004
2. Comment résoudre appliquer des problèmes de mathématiques l. Maiseiwitsch. Couer Corporation, 10 avril. 2013
3. Concepts de base de la géométrie. Walter Prenowz, Meyer Jordan. Rowman & Littlefield, 4 octobre. 2012
4. Les vecteurs. Rocío Navarro Lacoba, 7 juin. 2014
5. Algèbre linéaire. Bernard Kolman, David R. COLLINE. Pearson Education, 2006