Calcul du vecteur qui en résulte, exemples, exercices

Il vecteur résultant C'est celui obtenu par une opération avec des vecteurs dont le résultat est également un vecteur. Normalement, cette opération est la somme de deux ou plusieurs vecteurs, à travers lequel un vecteur est obtenu dont l'effet est équivalent.

De cette façon, des vecteurs tels que la vitesse, l'accélération ou la force sont obtenus. Par exemple, lorsque plusieurs forces agissent sur un corps F₁, F₂, F₃,.. . La somme vectorielle de toutes ces forces est équivalente à la force nette (la résultante), qui s'exprime mathématiquement:

F₁ + F₂ + F₃ +… = F_R  soit F_N

Figure 1. Le poids de la neige est distribué sur le plafond et son action peut être remplacée par une seule force résultant appliquée à l'endroit approprié. Source: Pixabay.

Le vecteur résultant, qu'il s'agisse de forces ou de toute autre ampleur vectorielle, applique les règles de la somme des vecteurs. Comme les vecteurs ont une direction et un sens en plus de la valeur numérique, il ne suffit pas d'ajouter les modules pour avoir le vecteur résultant.

Cela n'est vrai que dans le cas où les vecteurs impliqués sont dans la même direction (voir des exemples). Sinon, il est nécessaire d'utiliser des méthodes de somme vectorielle qui, selon le cas, peuvent être géométriques ou analytiques.

[TOC]

Exemples

Les méthodes géométriques pour trouver le vecteur résultant sont la méthode du polygone et la méthode parallélogramme.

Quant aux méthodes analytiques est la méthode des composants, à travers laquelle le vecteur résultant de tout système vectoriel peut être trouvé, tant que nous avons ses composants cartésiens.

Méthodes géométriques pour ajouter deux vecteurs

Supposons les vecteurs ou et V (Nous les désignons en gras pour les distinguer du scalaire). Dans la figure 2) nous les avons situés dans l'avion. Dans la figure 2 b), il est passé au vecteur V de telle manière que son origine coïncide avec la fin de ou. Le vecteur résultant va de l'origine du premier (ou) à la pointe du dernier (V):

Il peut vous servir: compressibilité: solides, liquides, gaz, exemples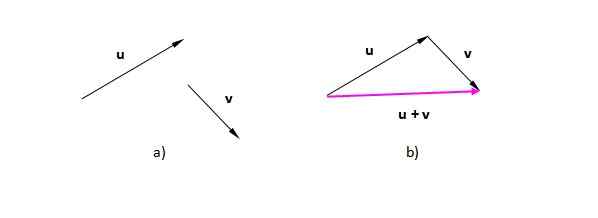 Figure 2. Le vecteur résultant de la somme graphique des vecteurs. Source: auto-faite.

La figure qui se traduit dans ce cas est un triangle (un triangle est un polygone à 3 faces). Si nous avons deux vecteurs dans la même direction, la procédure est la même: placez l'un des vecteurs après l'autre et dessinez l'un qui va de l'origine ou de la queue du premier à la pointe ou à la fin du dernier.

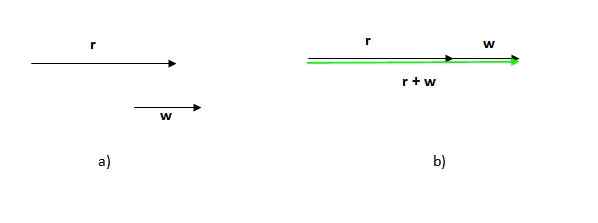
Notez que l'ordre dans lequel cette procédure est faite n'a pas d'importance, car la somme des vecteurs est commutative.

Notez également que dans ce cas le module (La longueur ou la taille) du vecteur résultant est la somme des modules des vecteurs supplémentaires, contrairement au cas précédent, dans lequel le module vectoriel résultant est inférieur à la somme des modules des participants.

Méthode de parallélogramme

Cette méthode est très appropriée lorsque vous devez ajouter deux vecteurs dont les points d'origine sont d'accord, avec l'origine d'un système de coordonnées X-Y. Supposons que ce soit le cas de nos vecteurs ou et V (Figure 3):

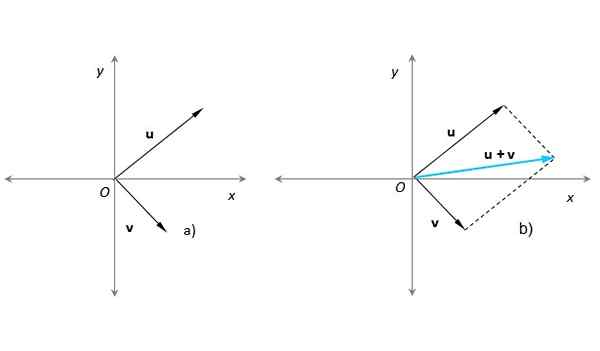figure 3. Somme de deux vecteurs au moyen de la méthode du parallélogramme avec le vecteur résultant en bleu turquoise. Source: auto-faite.

Dans la figure 3b), un parallélogramme a été construit à l'aide de lignes pointillées parallèles pour ou déjà V. Le vecteur résultant a son origine en O et sa fin au point où les lignes pointillées se croisent. Cette procédure est complètement équivalente à celle décrite dans la section précédente.

Exercices

-Exercice 1

Compte tenu des vecteurs suivants, trouvez le vecteur résultant en utilisant la méthode polygonale.

Il peut vous servir: réflexion légère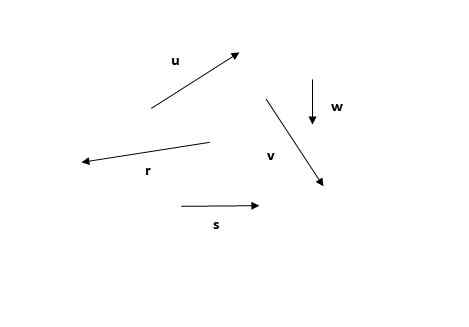 Figure 4. Vecteurs pour trouver sa méthode polygonale. Exercice 1. Source: auto-faite.

Solution

La méthode polygonale est la première des méthodes observées. N'oubliez pas que la somme des vecteurs est commutative (l'ordre des ajouts ne modifie pas la somme), vous pouvez donc commencer par l'un des vecteurs, par exemple ou (Figure 5a) ou r (Figure 5B):

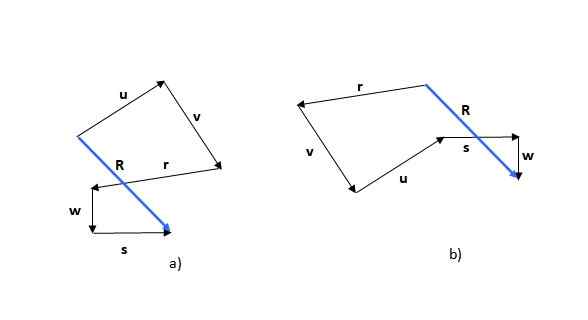Figure 5. Somme de vecteurs à travers la méthode polygonale. Source: auto-faite.

La figure obtenue est un polygone et le vecteur résultant (en bleu) est appelé R. Si vous commencez avec un autre vecteur, la figure formée peut être différente, comme on peut le voir dans l'exemple, mais le vecteur résultant est le même.

Exercice 2

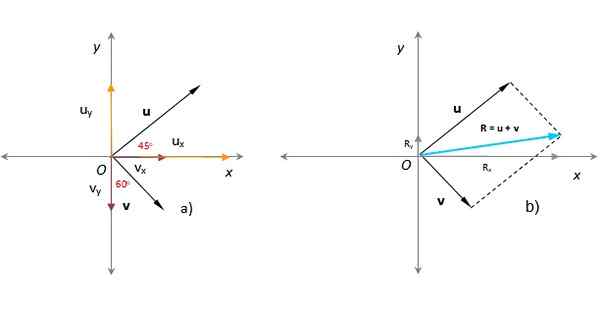
Dans la figure suivante, il est connu que les modules des vecteurs ou et V respectivement sont u = 3 unités arbitraires et v = 1.8 unités arbitraires. L'angle qui ou la forme avec l'axe x positif est de 45 º, tandis que V Formez 60 º avec l'axe y, comme on le voit sur la figure. Trouvez le vecteur, l'ampleur et la direction résultants.

Solution

Dans la section précédente, le vecteur résultant a été trouvé en appliquant la méthode de parallélogramme (en turquoise sur la figure).

Un moyen simple de trouver le vecteur résultant analytiquement consiste à exprimer les vecteurs ajoutant en termes de leurs composants cartésiens, ce qui est une tâche facile lorsque le module et l'angle sont connus, tels que les vecteurs de cet exemple:

ou_X = u . cos 45º = 3 x cos 45 º = 2.12 ou_et = u . péché 45 º = 3x sen 45º = 2.12

V_X = V . Sen 60º = 1.8 x sen 60 º = 1.56; V_et = -V . cos 60 º = -1.8 x cos 60º = - 0.9

Peut vous servir: mouvement pendulaire

Les vecteurs ou et V Ce sont des vecteurs appartenant à l'avion, ayant les deux composantes. Le vecteur U est dans le premier quadrant et ses composants sont positifs, tandis que le vecteur V est dans le quatrième quadrant; Sa composante x est positive, mais sa projection sur l'axe vertical tombe dans l'axe et négatif.

Calcul des composants cartésiens du vecteur résultant

Le vecteur résultant ajoute algébriquement les composants respectifs X et Y, pour obtenir ses composants cartésiens:

R_X = 2.12 + 1.56 = 3.68

R_et = 2.12 + (-0.9) = 1.22

Une fois les composants cartésiens spécifiés et le vecteur est complètement connu. Le vecteur résultant peut être exprimé avec la notation entre crochets (supports):

R = unités arbitraires

La notation du support est utilisée pour distinguer un vecteur d'un point dans le plan (ou dans l'espace). Une autre façon d'exprimer le vecteur résultant de manière analytique consiste à utiliser les vecteurs unitaires Toi et J dans l'avion (Toi, J et k dans l'espace):

R = 3.68 Toi + 1.22 J unités arbitraires

Étant donné que les deux composants du vecteur résultant sont positifs, le vecteur R Il appartient au premier quadrant, qui avait déjà été vu graphiquement.

Amplitude et direction du vecteur résultant

Connu des composants cartésiens, l'ampleur de R est calculée à travers le théorème de Pythagore, depuis le vecteur résultant R, à côté de ses composants r_X et r_et Ils forment un triangle droit:

Magnitude ou module: r = (3.68² + 1.22²)^½ = 3.88

Adresse Q prenant l'axe x positif comme référence: q = arcan (r_et / R_X) = arctg (1.22/3.68) = 18.3e

Les références

1. Ajout de vecteurs et de règles. Récupéré de: Newt.Chèque.UNSW.Édu.Au
2. Figueroa, D. Série: Physique pour la science et l'ingénierie. Volume 1. Cinématique.31-68.
3. Physique. Module 8: vecteurs. Récupéré de: Frtl.UTN.Édu.ardente
4. Hibbeler, R. 2006. Mécanique pour les ingénieurs. Statique. 6e édition. Société de rédaction continentale. 15-53.
5. Vector de calculatrice d'ajout. Récupéré de: www.1728.org