Trinôme carré parfait

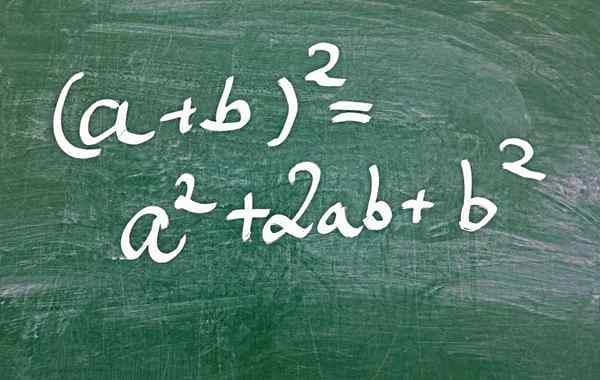Figure 1.- L'une des façons d'obtenir un trinôme carré parfait est le carré de la somme

Quel est le trinôme carré parfait?

Le trinôme carré parfait est que le polynôme de trois termes, dont deux sont des carrés parfaits des quantités a et b et sont précédés du même signe, tandis que le troisième terme est exactement le double produit de A et B, pouvant être de Un signe différent.

Un trinôme carré parfait est obtenu par carré la somme ou la différence d'un binôme et algébriquement, sa forme est la suivante:

pour² ± 2 ∙ AB + B²

Comme on peut le voir, le trinomial carré parfait contient:

• Deux termes quadratiques non similaires précédés du même signe: un² et B²
• Un troisième terme 2 ∙ AB, qui est le double produit des racines carrées des termes quadratiques et qui peut être précédé d'un signe positif ou négatif.

Les trinomiaux carrés parfaits peuvent être une ou plusieurs variables. Par exemple, le trinôme suivant est un carré parfait d'une variable:

• X² + 6x + 9

Notez que les premiers termes (x²) et le troisième (9) sont respectivement carrés des quantités appelées a et b. En effet, x² C'est le carré de x et 9 est le carré de 3. De cette façon, vous pouvez écrire ce qui suit:

a = x

B = 3

Et le terme restant est le double produit de x et 3:

6x = 2 ∙ 3 ​​∙ x

Une fois la vérification effectuée, il est certain que ce trinomial est un carré parfait.

Exemples

Figure 2.- Exemples de trinomiaux carrés parfaits. Source: F. Zapata.

Les trinomiaux carrés parfaits apparaissent également dans deux variables ou plus, par exemple:

4x² + 4xy + et²

C'est un trinôme en deux variables: "x" et "y". On peut assurer qu'il s'agit d'un trinôme carré parfait, car il présente deux termes quadratiques:

4x² = (2x)²

et² = (y)²

Et le terme restant est le double produit des racines carrées respectives: "2x" et "y":

Peut vous servir: Orthoedro: formules, zone, volume, diagonale, exemples

4xy = 2 ∙ 2x ∙ et

Les trinomiaux présentés jusqu'à présent sont de 2e année dans la variable "x", mais ils ne doivent pas nécessairement être comme ça. Le trinôme suivant est de 4e année dans "x":

9x⁴ - 30x²Yz + 25y²z²

Il est facilement vérifié qu'il s'agit d'un trinôme carré parfait. Le premier terme est le parfait carré 3x², Depuis (3x²)² = 9x⁴.

Le terme 25 ans²z² est égal à (5Yz)². Enfin, le terme restant est de 2 ∙ 3x²∙ 5 ans = 30 x²et Z.

D'un autre côté, les trinomiaux illustrés ci-dessous ne sont pas des trinomiaux carrés parfaits:

• X²  + 8x - 16

Ce n'est pas un trinôme carré parfait car 16, bien qu'il soit 4², Il est précédé d'un signe négatif, tandis que l'autre terme quadratique (x²) est positif.

• X²  - 15x + 25

Ce n'est pas non plus un trinôme carré parfait, car bien qu'il ait deux termes quadratiques: x² et 5², Le terme 15x n'est pas égal à 2 ∙ 5 ∙ x.

• 4x²  + 10x + 32

Ce trinomial n'est pas un carré parfait, car il ne contient qu'un terme quadratique: 4x² = (2x)².

Carré d'une somme et carré d'une différence

Les trinomiaux carrés parfaits sont obtenus en développant deux types de produits notables:

• Le carré de la somme.
• Le carré de la différence.

Le développement est d'abord obtenu à partir de la propriété distributive, car élever le binôme carré signifie le multiplier avec lui-même:

(A ± B)² = (a ± b) × (a ± b) = a² ± a ∙ b ± b ∙ a + b² = A² ± 2A ∙ B + B²

Le trinôme obtenu est un résultat qui est mémorisé avec juste un peu de pratique et est une sorte de raccourci qui facilite le développement, c'est pourquoi il est appelé un produit remarquable.

Peut vous servir: Nombres transcendants: quelles sont les formules, les exemples, les exercices

Les trinomials suivants sont facilement obtenus par un produit notable, sans ré-application de la propriété distributive.

• (x + 6)² = x² + 2 ∙ 6 ∙ x + 6² = x² + 12x + 36
• (2x - 10)² = (2x)² - 2 ∙ 10 ∙ 2x + 10² = 4x² - 40x + 100
• (5y + 2x)² = (5y)² + 2 ∙ 5y ∙ 2x + (2x)² = 25 et² +20xy + 4x²

Factorisation d'un trinôme carré parfait

Une opération fréquente et nécessaire dans l'algèbre est la factorisation du trinôme carré parfait, à travers lequel le trinomial est exprimé comme le carré d'une somme ou une soustraction de deux termes (un binomial).

Il est de l'opération inverse de développer le produit notable, car ayant le trinôme résultant, l'idée est d'obtenir le binomial qui lui donne naissance lorsqu'il monte au 2.

Par exemple, dans le 4x Perfect Square Trinomial précédemment analysé² + 4xy + et², Quel est le binomial que lorsqu'il est au carré, il vous donne naissance?

Les racines carrées respectives des termes quadratiques sont:

√ (4x²) = 2x

Ce qui équivaut à: 4x² = (2x)²

√ (et²) = y

Équivalent à dire cela: et² = (y)²

Donc:

4x² + 4xy + et² = (2x + y)²

Et quel est le binomial qui provient du trinomial carré parfait 9x⁴ - 30x²Yz + 25y²z²? Encore une fois, les racines carrées des termes quadratiques sont extraites:

√ (9x⁴) = 3x²

√ (25 et²z²) = 5 ans

Ensuite:

(3x² - 5 ans)² = 9x⁴ - 30x²Yz + 25y²z²

Exercices résolus

Exercice 1

Dans chacun des trinomials suivants, complétez le blanc avec le terme qui manque pour être un trinôme carré parfait:

suis² + 18m + _____

b) 4x² - _____ + 64

c) _____ + 30n + 25

• Solution à

Selon la formule du produit notable:

Peut vous servir: angles complémentaires: qui et comment ils sont calculés, exemples, exercices

(A ± B)² = A² ± 2A ∙ B + B²

Du trinôme:

m² + 18m + _____

Il s'ensuit:

a = m (pour que² = m²)

De plus, le terme central est: 2 ∙ a ∙ b = 2m ∙ b = 18m, donc b = 9 et son carré est 9² = 81. Guy par la formule du produit notable, le trinôme est comme ceci:

(M + 9)² = M² + 18m + 81

• Solution B

Dans ce trinôme:

4x² - _____ + 64

Vous pouvez savoir et b:

A = √ (4x²) = 2x

B = √64 = 8

Par conséquent, le terme manquant est le double produit de A et B:

2 ∙ AB = 2 ∙ 8 ∙ 2x = 32x

Et le trinôme recherché est:

4x² - 32x + 64

• Solution C

Dans le trinôme:

_____ + 30n + 25

Le premier terme est manquant, mais on sait que:

B = √25 = 5

ET

2 ∙ AB = 2 ∙ A ∙ 5 = 10A = 30N

Par conséquent, a = 3n et le trinôme recherché est:

9n² + 30n + 25

Exercice 2

Vérifiez que le suivant est un trinôme carré parfait et factez-le:

16 ans² - 24 ans + 9z²

• Solution

Il est d'abord prouvé que les termes quadratiques sont précédés du même signe, puis les racines carrées respectives sont trouvées:

A = √ (16y²) = 4y

B = √ (9Z²) = 3Z

Ensuite, vous devez vérifier si le terme restant est le double produit de A et B:

2 ∙ AB = 2 ∙ 4y ∙ 3Z = 24 ans

Si c'est le cas, le trinôme peut être facteur comme carré d'une différence, car le terme central est précédé d'un signe négatif:

16 ans² - 24 ans + 9z² = (4y - 3z)²

Les références

1. Jiménez, R. 2008. Algèbre. Prentice Hall.
2. Les leçons de mathématiques de Kate. Trinomiaux carrés parfaits. Récupéré de: Katesmathlessons.com.
3. Stewart, J. 2006. Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
4. Zill, D. 2008. Précculement avec avancées de calcul. 4e. Édition. McGraw Hill.