Propriétés transformées discrètes de Fourier, applications, exemples

La Fourier discret transformé Il s'agit d'une méthode numérique utilisée pour définir des échantillons liés aux fréquences spectrales qui composent un signal. Étudie les fonctions périodiques dans les paramètres fermés, jetant en conséquence un autre signal discret.

Afin d'obtenir la transformation discrète de Furier de n points, sur un signal discret, les 2 conditions suivantes sur une séquence doivent être remplies X [n]

 x [n] = 0   N n - 1

Remplissant ces conditions, la transformation discrète de Fourier peut être définie comme

TDF

La transformation discrète de Fourier peut être définie comme un échantillonnage en n points de la transformation de Fourier.

[TOC]

Interprétation de la transformation discrète de Fourier

Source: Pexels

Il y a 2 points de vue à partir desquels les résultats obtenus sur une séquence X peuvent être interprétés_s[n] à travers la transformation discrète de Fourier.

-Le premier correspond aux coefficients spectraux, déjà connus de la série Fourier. Il est observé dans des signaux périodiques discrets, avec des échantillons coïncidant avec la séquence x_s[N].

-La seconde concerne le spectre d'un signal d'ouverture discret, avec des échantillons correspondant à la séquence x_s[N].

La transformation discrète est une approche du spectre du signal analogique d'origine. Sa phase dépend des moments d'échantillonnage, tandis que sa magnitude dépend de l'intervalle d'échantillonnage.

Propriétés

Les fondations algébriques de la structure constituent la base logique des sections suivantes.

Linéarité

C . S_n → C . F[S_k]] Si une séquence est multipliée par un scalaire, sa transformation sera également.

T_n + V_n = F [t_k] + F [V_k]] La transformée d'une somme est égale à la somme de celle transformée.

Dualité

F [s_n] → (1 / n) s_-K; Si la transformée discrète de Fourier est rappelée en une expression déjà transformée, la même expression est obtenue, grimpant en n inversé par rapport à l'axe vertical.

Convolution

Chassant des objectifs similaires que dans la transformée de Laplace, la convolution des fonctions fait référence au produit parmi ses transformations de Fourier. La convolution s'applique également à des temps discrets et est responsable de nombreuses procédures modernes.

X_n * R_n → F [x_n]] .F [r_n]] La transformée d'une convolution est égale au produit de ceux transformés.

X_n . R_n→ F [x_n] * F [r_n]] La transformée d'un produit est égale à la convolution des transformés.

Déplacement

X_N-m → F [x_k] e ^{-I (2π / n) km} ; Si une succession est retardée dans les échantillons de M, son effet sur la transformation discrète sera une modification de l'angle défini par (2π / n) km.

Peut vous servir: pourquoi l'algèbre est-elle importante dans certaines situations de vie quotidiennes?

Symétrie conjugué

X_t [-K] = x *_t[k] = x_t [N - k]

Modulation

W^-nm_N . x [n] ↔ x_t[K - m]

Produit

x [n] y [n] ↔ (1 / n) x_t[k] * et_t[K]

Symétrie

X [-n] ↔ x_t[-K] = x *_t[K]

Conjuguer

x * [n] ↔ x *_t[-K]

Équation de Parseval 

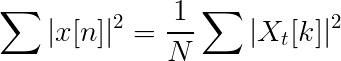
Similitudes et différences avec la transformée de Fourier

En ce qui concerne la transformée conventionnelle de Fourier, il a plusieurs similitudes et différences. La transformation de Fourier convertit une séquence en une ligne continue. De cette façon, il est dit que le résultat de la variable de Fourier est une fonction variable réelle complexe.

La transformation discrète de Fourier, contrairement, reçoit un signal discret et le transforme en un autre signe discret, c'est-à-dire une séquence.

Quelle est l'utilisation de la transformation discrète de Fourier?

Ils servent principalement à des équations importantes, tout en transformant des expressions dérivées en éléments de puissance. Indiquant des expressions différentielles sous des formes de polynômes intégrables.

Dans l'optimisation, la modulation et la modélisation des résultats, il agit comme une expression standardisée, étant une ressource fréquente pour l'ingénierie après plusieurs générations.

Source: Pixabay

Histoire

Ce concept mathématique a été présenté par Joseph B. Fourier en 1811, tout en développant un traité concernant le Se propager. Il a été rapidement adopté par diverses branches de la science et de l'ingénierie.

Il a été établi comme le principal outil de travail dans l'étude des équations avec des dérivés partiels, comparant même avec la relation de travail entre le Laplace transformée et équations différentielles ordinaires.

Toute fonction qui peut être travaillée avec Fourier Transform doit présenter une nullité en dehors d'un paramètre défini.

Fourier discret transformé et son inverse

La transformation discrète est obtenue par l'expression:

Après une séquence discrète x [n]

L'inverse de la transformation discrète de Fourier est défini par l'expression:

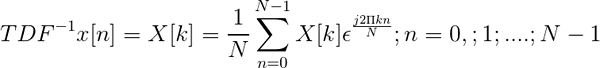TDF inverse

Il permet une fois que le discret transformé, définissez la séquence dans le domaine temporel x [n].

Atours

Le processus de paramétrage correspondant à la transformation discrète de Fourier réside dans le Cub. Pour travailler la transformation, nous devons limiter la séquence dans le temps. Dans de nombreux cas, les signaux en question n'ont pas ces limites.

Une succession qui ne répond pas aux critères de taille à s'appliquer à la transformation discrète, peut être multiplié par une fonction «fenêtre» v [n], définissant le comportement de la succession dans un paramètre contrôlé.

Peut vous servir: permutations circulaires: démonstration, exemples, exercices résolus

X [n] . V [n]

La largeur du spectre dépendra de la largeur de la fenêtre. À mesure que la largeur de la fenêtre augmente, la transformée calculée sera plus étroite.

Applications

Calcul de la solution fondamentale

La transformation discrète de Fourier est un outil puissant dans l'étude des successions discrètes.

La transformation discrète de Fourier transforme une fonction variable continue, en une transformation variable discrète.

Le problème de Cauchy pour l'équation thermique présente un champ d'application fréquent de la transformation discrète de Fourier. Où la fonction est générée Heat de Dirichlet ou noyau central, qui s'applique à l'échantillonnage des valeurs dans un paramètre défini.

Théorie du signal

La raison générale de l'application de la transformation discrète de Fourier dans cette branche est principalement due à la décomposition caractéristique d'un signal en tant que chevauchement infini de signaux plus facilement traitables.

Il peut s'agir d'une onde sonore ou d'une onde électromagnétique, la transformée discrète de Fourier l'exprime dans un chevauchement d'onde simple. Cette représentation est assez fréquente en génie électrique.

Série de Fourier

Ce sont des séries définies en termes de cosenos et de seins. Ils servent à faciliter le travail avec des fonctions périodiques générales. Lorsqu'ils sont appliqués, ils font partie des techniques de résolution des équations différentielles partielles et ordinaires.

Les séries de Fourier sont encore plus générales que la série de Taylor, car ils développent des fonctions de discontinua périodiques qui n'ont aucune représentation dans la série Taylor.

Autres formes de la série Fourier

Pour comprendre analytiquement la transformation de Fourier, c'est important.

-Série de Fourier sur une fonction de période de 2L:

Plusieurs fois, il est nécessaire d'adapter la structure d'une série de Fourier, à des fonctions périodiques dont la période est p = 2l> 0 dans l'intervalle [-l, l].

-Série de Fourier dans des fonctions uniques et étranges

L'intervalle [-π, π] est pris en compte qui offre des avantages lors de la mise en profit des caractéristiques symétriques des fonctions.

Peut vous servir: ensemble fini: propriétés, exemples, exercices résolus

Si F Is Torque, la série Fourier est établie comme une série de cosenos.

Si F est étrange, la série Fourier est établie comme une série de seins.

-Notation complexe de la série Fourier

Si vous avez une fonction F (t), qui répond à toutes les exigences de la série Fourier, il est possible de le désigner dans l'intervalle [-t, t] en utilisant sa notation complexe: 

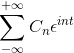
Exemples

En ce qui concerne le calcul de la solution fondamentale, les exemples suivants sont présentés:

Équation de Laplace

Équation thermique

Équation de Schrödinger

Équation des vagues

D'un autre côté, il existe des exemples d'application de la transformation discrète de Fourier dans le domaine de la théorie du signal:

-Problèmes d'identification du système. Établi F et G

-Problème avec la cohérence du signal de sortie

-Problèmes avec le filtrage du signal

Exercices

Exercice 1

Calculez la transformée discrète de Fourier pour la succession suivante.

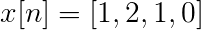
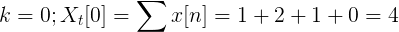
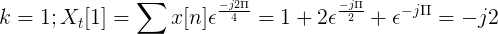
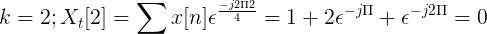
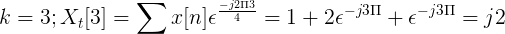
Le TDF x [n] peut être défini comme:

X_t[k] = 4, -j2, 0, j2 pour k = 0, 1, 2, 3

Exercice 2

Il est voulu déterminer à travers un algorithme numérique le signal spectral défini par l'expression x (t) = e^-t. Où le coefficient de demande de fréquence maximale est f_m= 1Hz. Une harmonique correspond à F = 0.3 Hz. L'erreur est limitée à moins de 5%. Calculer F_s , D et N.

Compte tenu du théorème d'échantillonnage F_s = 2f_m = 2 Hz

Une résolution de fréquence de F₀ = 0.1 Hz, où d = 1 / 0,1 = 10s sont obtenus

0.3 Hz est la fréquence correspondant à l'index k = 3, où n = 3 × 8 = 24 échantillons. Indiquant que F_s = N / d = 24/10 = 2.4> 2

Parce que le but est d'atteindre la valeur la moins possible pour n, les valeurs suivantes peuvent être considérées comme une solution:

F₀ = 0.3 Hz

D = 1/0.3 = 3.33

K = 1

N = 1 × 8 = 8

Les références

1. Master la transformation discrète de Fourier en une, deux ou plusieurs dimensions: les pièges et les artefacts. Isaac Amidor. Springer Science & Business Media, 19 juillet. 2013
2. Le DFT: un manuel des propriétaires pour la transformée de Fourier discrète. William L. Briggs, van Emden Henson. Siam, 1er janvier. Année mille neuf cents quatre-vingts-quinze
3. Traitement du signal numérique: théorie et pratique. D. Sundararajan. World Scientific, 2003
4. Transforme et algorithmes rapides pour l'analyse et les représentations du signal. Guoan BI, Yonghong Zeng. Springer Science & Business Media, 6 décembre. 2012
5. Transformes de Fourier discrètes et continues: analyse, applications et algorithmes rapides. Eleanor Chu. CRC Press, 19. 2008