transformation de Laplace

Quelle est la transformation de Laplace?

La transformation de Laplace Il a été de ces dernières années d'une grande importance dans l'ingénierie, les mathématiques, la physique, entre autres domaines scientifiques, car en plus d'être d'un grand intérêt pour le théorique, il fournit un moyen simple de résoudre les équations différentielles, les transformant en équations algébriques.

À l'origine, la transformée de Laplace a été présentée par Pierre-Simon Laplace (1745-1827) dans son étude sur la théorie de la probabilité, et en principe a été traité comme un objet mathématique d'un simple intérêt théorique.

Les applications actuelles surviennent lorsque divers mathématiciens ont tenté de donner une justification formelle aux «règles opérationnelles» utilisées par Oliver Heaviside (1850-1925) dans l'étude des équations de la théorie électromagnétique.

Définition de la transformée de Laplace

Soit F une fonction définie pour t ≥ 0. La transformée de Laplace est définie comme suit:

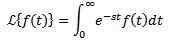
On dit que la transformée de Laplace existe si l'intégrale précédente converge, sinon il est dit que la transformée de Laplace n'existe pas.

En général, pour désigner la fonction qui est souhaitée pour transformer de minuscules lettres et la lettre majuscule correspond à sa transformation. De cette façon, nous aurons:

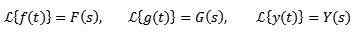
Exemples

Considérez la fonction constante f (t) = 1. Nous devons nous transformer:

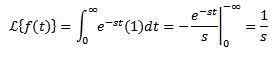
À condition que l'intégrale converge, c'est-à-dire à condition que S> 0. Sinon, s < 0, la integral diverge.

Soit g (t) = t. Sa transformée de Laplace est donnée par:

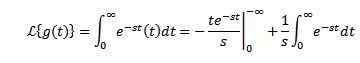
Lors de l'intégration par des parties et de savoir que^-St Il tend à 0 lorsque t tend à l'infini et s> 0, avec l'exemple précédent, nous devons:

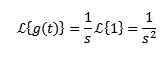
Le transformateur peut exister ou non, par exemple pour la fonction f (t) = 1 / t, l'intégrale qui définit sa transformation de Laplace ne converge pas et donc sa transformée n'existe pas.

Les conditions suffisantes pour garantir que la transformée de la Laplace d'une fonction F existe, est que F est continu en parties pour T ≥ 0 et est d'un ordre exponentiel.

On dit qu'une fonction est continue en parties pour t ≥ 0, quand pour un intervalle [a, b] avec un> 0, il y a un nombre fini de points t_k, Où f a des discontinuités et est continu dans chaque sous-intervalle [t_K-1,t_k]].

D'un autre côté, il est dit qu'une fonction exponentielle C s'il y a de vraies constantes m> 0, c et t> 0 telles que:

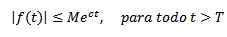
Comme exemples, nous devons f (t) = t² C'est exponentiel, puisque | t²| < e^3T Pour tous les t> 0.

Nous avons officiellement le théorème suivant:

Théorème (conditions suffisantes pour l'existence)

Si f est une fonction continue pour T> 0 et C exponentielle, alors il y a la transformée de Laplace pour S> C.

Il est important de souligner qu'il s'agit d'une condition de suffisance, c'est-à-dire qu'il pourrait y avoir un cas qu'il existe une fonction qui ne remplit pas ces conditions et pourtant sa transformée de Laplace existe.

Un exemple de ceci est la fonction f (t) = t^-1/2 qui n'est pas continu en parties pour t ≥ 0 mais sa transformée de Laplace existe.

Laplace Transforment de certaines fonctions de base

Le tableau suivant montre les transformations de Laplace des fonctions les plus courantes.

Peut vous servir: nombres entiers

Histoire de la transformée de Laplace

La transformée de Laplace doit son nom en Pierre-Simon Laplace, mathématicien et astronome et théoricien français qui est né en 1749 et décédé en 1827. Sa renommée était telle qu'il était connu comme le Newton en France.

En 1744, Leonard Euler (1707-1783) a consacré ses études aux intégrales avec la forme

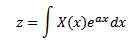
comme des solutions d'équations différentielles ordinaires, mais ont rapidement abandonné cette recherche. Plus tard, Joseph Louis Lagrange (1736-1813), qui a beaucoup admiré Euler, a également étudié ce type d'intégrale et les a liés à la théorie de la probabilité.

1782, Laplace

En 1782, Laplace a commencé à étudier ces intégrales comme solutions à des équations différentielles et, selon les historiens, en 1785, il décida de reformuler le problème, qui a ensuite donné naissance aux transformations de Laplace telles qu'elles sont comprises aujourd'hui.

Ayant été introduit dans le domaine de la théorie des probabilités, il ne s'intéressait à que les scientifiques du moment et n'étaient considérés que comme un objet mathématique uniquement d'intérêt théorique.

Huile Oliver

C'était au milieu du niveau du niveau du milieu du siècle que l'ingénieur anglais Oliver Heaviside a découvert que les opérateurs différentiels peuvent être traités comme des variables algébriques, donnant ainsi leur application moderne aux transformations de Laplace.

Oliver Heaviside était un physicienne, ingénieur en anglais et mathématique, né en 1850 à Londres et décédé en 1925. Tout en essayant de résoudre des problèmes d'équations différentielles appliquées à la théorie des vibrations et en utilisant des études de Laplace, il a commencé à façonner les applications modernes de Lapla Transforts.

Les résultats exposés par le tas se propagent rapidement.

Cependant, l'utilité du travail de Heaviside lors de la résolution des équations de physique a rendu populaire leurs méthodes entre les physiciens et les ingénieurs.

Malgré ces revers et après quelques décennies de tentatives infructueuses, au début du 20e siècle, il pourrait être donné une justification rigoureuse aux règles opérationnelles établies par Heaviside.

Ces tentatives ont porté leurs fruits grâce aux efforts de divers mathématiciens, comme Bromwich, Carson, Van der Pol, entre autres.

Propriétés de transformation de Laplace

Parmi les propriétés de la transformée de Laplace, la suivante se démarque:

Linéarité

Soit les fonctions C1 et C2 constantes et f (t) et g (t) dont les transformations de Laplace sont respectivement F (s) et g (s), alors il doit:

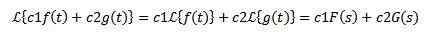
En raison de cette propriété, il est dit que la transformée de Laplace est un opérateur linéaire.

Exemple:

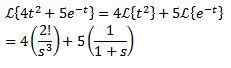
Théorème de la première traduction

Si cela arrive:

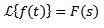
Et «a» est tout nombre réel, alors:

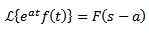
Exemple:

Comme le Laplace de cos transforme (2T) = S / (S ^ 2 + 4) alors:

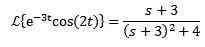
Deuxième théorème de traduction

Ouais

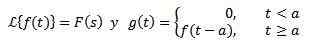
Ensuite

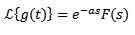
Exemple:

Si f (t) = t ^ 3, alors f (s) = 6 / s ^ 4. Et donc, la transformation de 

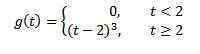
est g (s) = 6e^-2s/ s ^ 4

Changement d'échelle

Ouais

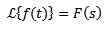
Et «a» est réel de zéro, nous devons

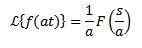
Exemple:

Comme la transformation de f (t) = sen (t) est f (s) = 1 / (s ^ 2 + 1)

Peut vous servir: Notation développée: quels sont les exemples et les exercices

Laplace transformé des dérivés

Si f, f ', f ", ..., f^(N) Ils sont continus pour t ≥ 0 et sont exponentiels et f^(N)(t) est continu en parties pour t ≥ 0, puis

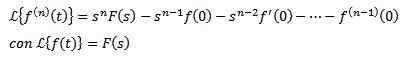
Transformée de laplace intégrale

Ouais

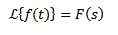
Ensuite

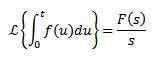
Multiplication par tⁿ

Si nous devons

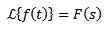
Ensuite

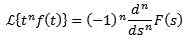
Division par t

Si nous devons

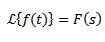
Ensuite

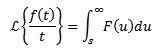
Fonctions périodiques

Soit f une fonction périodique avec la période t> 0, c'est-à-dire f (t + t) = f (t), puis

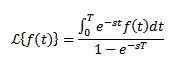
Comportement de f (s) lorsque s tend à l'infini

Si f est continu en parties et en ordre exponentiel et

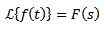
Ensuite

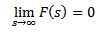
Inverse transformé

Lorsque nous appliquons la transformée de Laplace en une fonction F (t), nous obtenons F (s), qui représente ladite transformée. De la même manière, nous pouvons dire que F (t) est la transformée du Laplace inverse de F (S), et est écrit comme

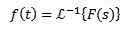
Nous savons que les transformations de Laplace de f (t) = 1 et g (t) = t sont f (s) = 1 / s et g (s) = 1 / s² respectivement, donc nous devons

Certains laplace communs transformés sont les suivants

De plus, la transformée inverse de Laplace est linéaire, c'est-à-dire qu'il est accompli que

Exercer

Trouver

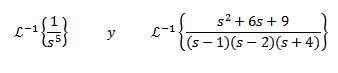
Pour résoudre cet exercice, nous devons faire correspondre la fonction F (s) avec une partie du tableau précédent. Dans ce cas, si nous prenons n + 1 = 5 et en utilisant la propriété de linéarité de la transformation inverse, nous multiplions et divisons par 4! Obtenir

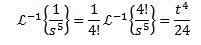
Pour la deuxième transformée inverse, nous appliquons des fractions partielles pour réécrire la fonction F (s) puis la propriété de la linéarité, obtenant

Comme nous pouvons le voir à partir de ces exemples, il est courant que la fonction F (s) qui est évaluée ne correspond pas précisément à aucune des fonctions données dans le tableau. Pour ces cas, comme observé, il suffit de réécrire la fonction jusqu'à ce qu'elle atteigne la forme appropriée.

Applications de transformation de Laplace

Équations différentielles

La principale application que les transformes de Laplace possèdent est de résoudre les équations différentielles.

En utilisant la propriété de la transformation d'un dérivé, il est clair que

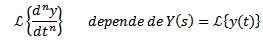
Et du n-1 dérivé évalué à t = 0.

Cette propriété rend la transformée.

Les exemples suivants montrent comment utiliser la transformée de Laplace pour résoudre les équations différentielles.

Exemple 1

Compte tenu du problème de valeur initiale suivante

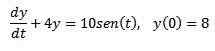
Utilisez la transformée de Laplace pour trouver la solution.

Nous appliquons la transformée de Laplace à chaque membre de l'équation différentielle

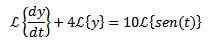
Pour la propriété de la transformation d'un dérivé que nous avons

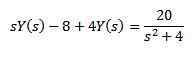
Lors du développement de toute l'expression et de la compensation et (s) nous avons

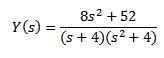
En utilisant des fractions partielles pour réécrire le côté droit de l'équation que nous obtenons

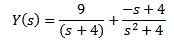
Enfin, notre objectif est de trouver une fonction et (t) qui satisfait l'équation différentielle. L'utilisation de la transformation inverse de Laplace, il en résulte

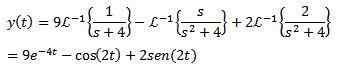
Exemple 2

Résoudre

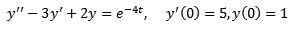
Comme dans le cas précédent, nous appliquons la transformée des deux côtés de l'équation et du terme séparé.

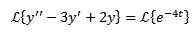
De cette façon, nous avons en conséquence

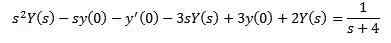
Remplacement par les valeurs initiales données et la compensation et (S)

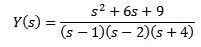
En utilisant des fractions simples, nous pouvons réécrire comment l'équation suit

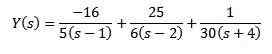
Et l'application de la transformée inverse de Laplace nous donne en conséquence

Dans ces exemples, la mauvaise conclusion a pu être conclue que cette méthode n'est pas beaucoup meilleure que les méthodes traditionnelles pour résoudre les équations différentielles.

Peut vous servir: proportion

Les avantages offerts par la transformation de Laplace est qu'il n'est pas nécessaire.

De plus, lors de la résolution des problèmes de valeur initiale par cette méthode, depuis le début, nous utilisons les conditions initiales, il n'est donc pas nécessaire d'effectuer d'autres calculs pour trouver la solution particulière.

Systèmes d'équations différentielles

La transformée de Laplace peut également être utilisée pour trouver des solutions à des équations différentielles ordinaires simultanées, comme le montre l'exemple suivant.

Exemple

Résoudre

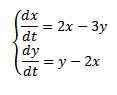
Avec les conditions initiales x (0) = 8 e y (0) = 3.

Si nous devons

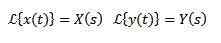
Ensuite

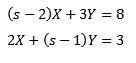
La résolution nous donne en conséquence

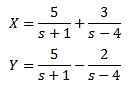
Et lors de l'application de la transformée inverse de Laplace, nous avons

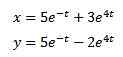
Mécanique et circuits électriques

La transformée de Laplace est d'une grande importance en physique, a principalement des applications pour la mécanique et les circuits électriques.

Un circuit électrique simple est composé des éléments suivants:

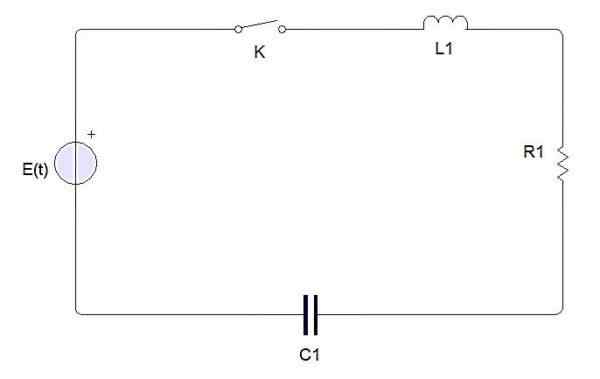Éléments d'un circuit électrique

Un interrupteur, une batterie ou une source, une inductance, une résistance et un condensateur. Lorsque l'interrupteur est fermé, un courant électrique indiqué par i (t). La charge de condensateur est indiquée par Q (t).

Par la deuxième loi de Kirchhoff, la tension produite par le fuente e au circuit fermé doit être égale à la somme de chacune des chutes de tension.

Le courant électrique i (t) est lié à la charge Q (t) dans le condensateur via i = dq / dt. D'un autre côté, la baisse de tension dans chacun des éléments est définie comme suit:

La chute de tension dans une résistance est IR = R (dq / dt)

La chute de tension dans une inductance est l (di / dt) = l (d²Q / DT²)

La chute de tension dans un condensateur est Q / C

Avec ces données et l'application de la deuxième loi de Kirchhoff au circuit simple simple, une équation différentielle du deuxième ordre est obtenue qui décrit le système et nous permet de déterminer la valeur de q (t).

Exemple

Une inductance, un condensateur et une résistance sont connectés à une batterie E, comme indiqué sur la figure. L'inductance est 2 Henries, le condensateur Farads de 0,02 et la résistance des 16 onhmios. Pour le moment, t = 0 ferme le circuit. Trouvez la charge et le courant à tout moment t> 0 si e = 300 volts.

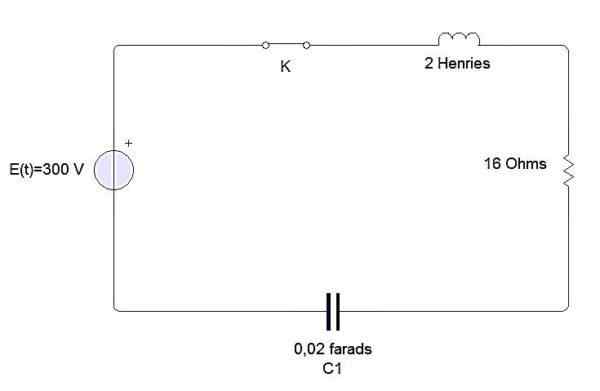
Nous avons que l'équation différentielle décrivant ce circuit est la suivante:

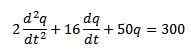
Où les conditions initiales sont q (0) = 0, i (0) = 0 = q '(0).

En appliquant la transformée de Laplace, nous obtenons cela

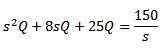
Et compenser Q (t)

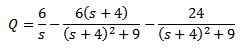
Ensuite, en appliquant la transformation inverse de Laplace que nous avons

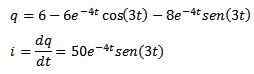
Les références

1. g.Holbrook, J. (1987). Transformée de Laplace pour les ingénieurs électroniques. Limusa.
2. Ruiz, L. M., & Hernandez, m. P. (2006). Équations différentielles et transformées de Laplace avec des applications. Editorial UPV.
3. Simmons, G. F. (1993). Équations différentielles avec applications et notes historiques. McGraw-Hill.
4. Spiegel, m. R. (1991). Laplace a transformé. McGraw-Hill.
5. Zill, D. g., & Cullen, M. R. (2008). Équations différentielles avec les valeurs des titres à la frontière. Cengage Learning Editoires, S.POUR.