Matematiques

Transformations isométriques

Le transformations isométriques Ce sont des changements de position ou d'orientation d'une certaine figure qui ne modifient pas la forme ou la taille de ce. Ces transformations sont classées en trois types: traduction, rotation et réflexion (isométrie). En général, les transformations géométriques permettent de créer une nouvelle figure à partir d'un autre donné.

Une transformation en une figure géométrique signifie que, d'une certaine manière, elle a été soumise à un certain changement; c'est-à-dire qu'il a été modifié. Selon le sens de l'original et du similaire dans le plan, les transformations géométriques peuvent être classées en trois types: isométrique, isomorphe et anamorphique.

Caractéristiques des transformations isométriques

- Les transformations isométriques se produisent lorsque les amplitudes des segments et des angles entre la figure d'origine et la figure transformée sont préservées.

- Dans ce type de transformation, la forme ou la taille de la figure n'est pas modifiée (elles sont congruents), ce n'est qu'un changement de position de cela, soit dans l'orientation, soit dans le sens. De cette façon, le chiffre initial et la finale seront similaires et congruents géométriquement.

- L'isométrie fait référence à l'égalité; c'est-à-dire que les chiffres géométriques seront isométriques s'ils ont la même forme et la même taille.

- Dans les transformations isométriques, la seule chose qui peut être observée est un changement de position dans le plan, un mouvement rigide se produit grâce à laquelle la figure passe d'une position initiale à une finale. Cette figure est appelée homologue (similaire) de l'original.

- Il existe trois types de mouvements qui classent une transformation isométrique: la traduction, la rotation et la réflexion ou la symétrie.

Types de transformations isométriques

Par traduction

Sont ces isométries qui permettent de déplacer en ligne droite tous les points de l'avion dans une direction et une distance spécifiques.

Lorsqu'une figure est transformée par traduction, elle ne change pas son orientation par rapport à la position initiale, ni ne perd ses mesures internes, les mesures de ses angles et de ses côtés. Ce type de déplacement est défini par trois paramètres:

Une adresse, qui peut être horizontale, verticale ou oblique.
Une direction, qui peut être à gauche, à droite, en haut ou en bas.
Distance ou ampleur, qui est la longueur qui est de la position initiale à la finale de tout point qui se déplace.

Peut vous servir: Curtosis: définition, types, formules, à quoi sert, par exemple

Pour une transformation isométrique due à la traduction, il doit répondre aux conditions suivantes:

La figure doit toujours conserver toutes ses dimensions, à la fois linéaire et angulaire.
La figure ne change pas sa position par rapport à l'axe horizontal; c'est-à-dire que son angle ne varie jamais.
Les traductions seront toujours résumées en une, quel que soit le nombre de traductions faites.

Dans un plan où le centre est un point ou, avec des coordonnées (0,0), la traduction est définie par un vecteur t (a, b), ce qui indique le déplacement du point initial. C'est-à-dire:

P (x, y) + t (a, b) = p '(x + a, y + b)

Par exemple, si au point de coordonnées P (8, -2), une traduction t (-4, 7) est appliquée, elle est obtenue:

P (8, -2) + t (-4, 7) = p '[(8 + (-4)), ((-2) + 7)] = p' (4, 5)

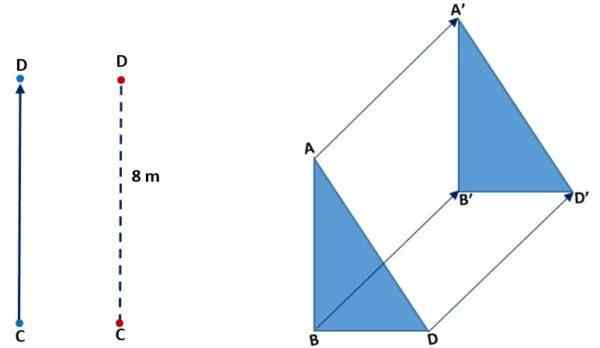
Dans l'image suivante (à gauche), vous pouvez voir comment le point C s'est déplacé pour coïncider avec le D. Il l'a fait verticalement, le sens a augmenté et le CD de distance ou de magnitude était de 8 mètres. Dans l'image droite, la traduction d'un triangle est observée:

Par rotation

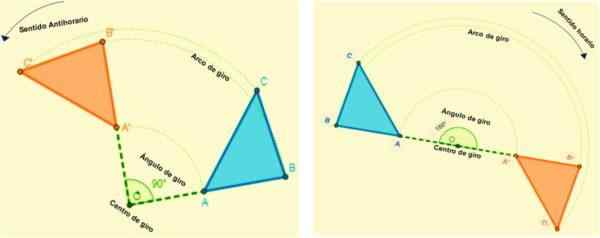
Sont ces isométries qui permettent à la figure de tourner tous les points d'un avion. Chaque point tourne après un arc qui a un angle constant et un point fixe (centre de virage) déterminé.

C'est-à-dire que toute rotation sera définie par son centre de rotation et d'angle de virage. Lorsqu'une figure est transformée par rotation, elle maintient la mesure de ses angles et de ses côtés.

La rotation se produit dans une certaine direction, elle est positive lorsque le virage est anti-horaire (contrairement à la façon dont les mains de l'horloge tournent) et négatives lorsque son virage est dans le sens horaire.

Si un point (x, y) est tourné par rapport à l'origine - c'est-à-dire, son centre de rotation est (0,0) -, à un angle de 90^soit 360^soit Les coordonnées des points seront:

Peut vous servir: branches statistiques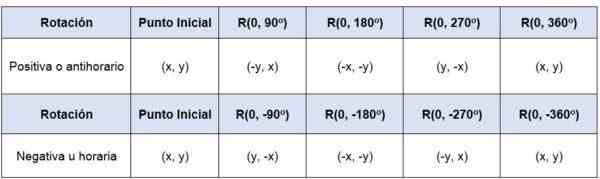

Dans le cas où la rotation n'a pas de centre à l'origine, l'origine du système de coordonnées à l'origine nouvelle donnée doit être transférée, afin de faire pivoter la figure ayant l'origine l'origine.

Par exemple, si le point P (-5,2), une rotation 90 est appliquée^soit, Autour de l'origine et dans un sens positif, ses nouvelles coordonnées seront (-2,5).

Par réflexion ou symétrie

Sont ces transformations qui investissent les points et les chiffres de l'avion. Cet investissement peut être par rapport à un point ou peut également être par rapport à une ligne.

En d'autres termes, dans ce type de transformation, chaque point de la figure d'origine est associé à un autre point (image) de la figure homologue, de sorte que le point et son image sont à la même distance d'une ligne appelée axe de symétrie.

Ainsi, la partie gauche de la figure sera le reflet du côté droit, sans changer sa forme ou ses dimensions. La symétrie transforme une figure égale mais en sens inverse, comme on peut le voir dans l'image suivante:

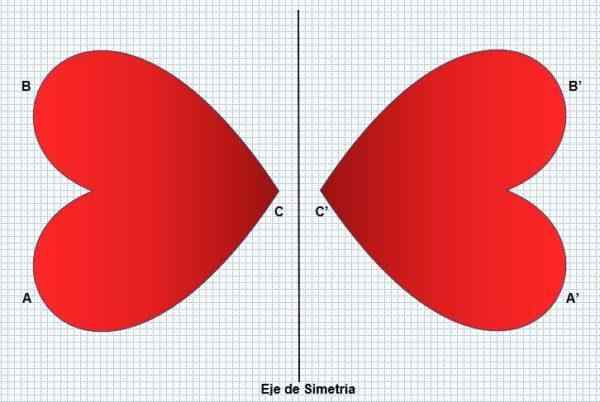
La symétrie est présente sous de nombreux aspects, comme certaines plantes (tournesols), les animaux (paon) et les phénomènes naturels (flocons de neige). L'être humain le reflète dans son visage, qui est considéré comme un facteur de beauté. La réflexion ou la symétrie peut être de deux types:

Symétrie centrale

C'est cette transformation qui se produit par rapport à un point, dans lequel la figure peut changer son orientation. Chaque point de la figure d'origine et de son image sont à la même distance d'un point ou, appelé centre de symétrie. La symétrie est centrale lorsque:

Le point et son image et son centre appartiennent à la même ligne.
Avec une rotation de 180^soit du centre ou une figure égale à l'original est obtenue.
Les traits de la figure initiale sont parallèles aux traits de la figure formée.
La signification de la figure ne change pas, elle sera toujours dans un calendrier.

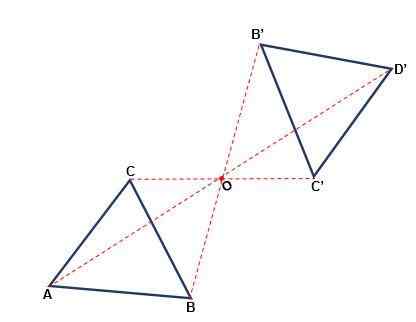Peut vous servir: combien devez-vous ajouter à 3/4 pour obtenir 6/7?

Symétrie axiale

Cette transformation se produit par rapport à l'axe de symétrie, où chaque point de la figure initiale est associé à un autre point de l'image et ceux-ci sont à la même distance que l'axe de symétrie. La symétrie est axiale lorsque:

Le segment qui rejoint un point avec son image est perpendiculaire à son axe de symétrie.
Les chiffres changent leur signification concernant le virage ou la direction du temps.
En divisant la figure avec une ligne centrale (axe de symétrie), l'une des moitiés résultantes coïncide complètement avec une autre moitié.

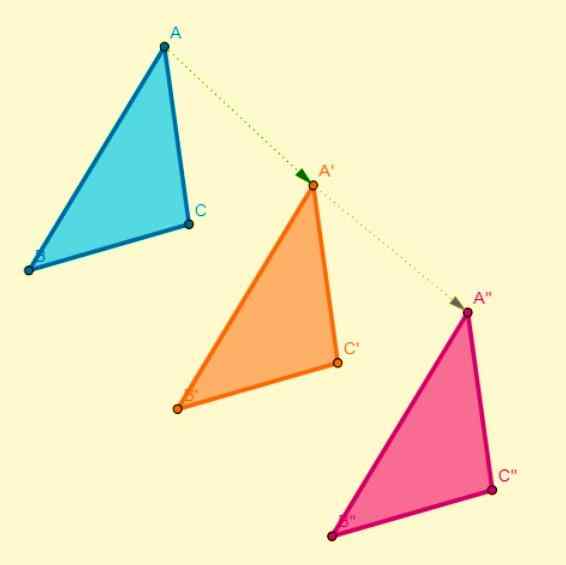
Composition

Une composition de transformations isométriques fait référence à l'application successive des transformations isométriques sur la même figure.

Composition d'une traduction

La composition de deux traductions entraîne une autre traduction. Lorsqu'il est effectué sur le plan, sur l'axe horizontal (x), seules les coordonnées de cet axe changent, tandis que les coordonnées de l'axe vertical (y) restent les mêmes, et vice versa.

Composition d'une rotation

La composition de deux tours avec le même centre se traduit par un autre tour, qui a le même centre et dont l'amplitude sera la somme des amplitudes des deux tours.

Si le centre du tour a un centre différent, la coupe des deux segments de points similaires sera le centre de rotation.

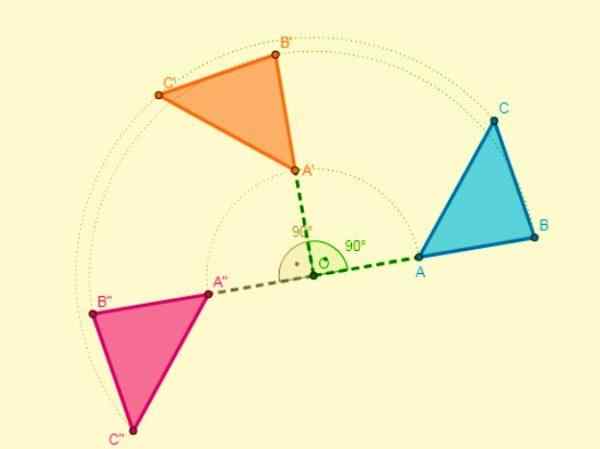
Composition de symétrie

Dans ce cas, la composition dépendra de la façon dont elle est appliquée:

Si la même symétrie est appliquée deux fois, le résultat sera une identité.
Si deux symétries sont appliquées par rapport à deux axes parallèles, le résultat sera la traduction et leur déplacement est le double de la distance de ces axes:

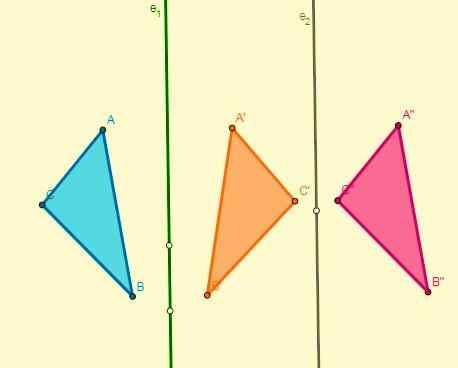
Si deux symétries sont appliquées par rapport à deux axes qui sont coupés au point O (centre), une rotation avec centre sera obtenue et son angle sera deux fois l'angle que les axes forment: