Formules de prise de vue verticales, équations, exemples

Il tir vertical C'est un mouvement qui se déroule sous l'action d'un champ de forces, généralement celui de la gravité, de pouvoir monter ou descendre. Il est également connu sous le nom de Lancement vertical.

L'exemple le plus immédiat est lancé (ou vers le bas si préféré) une balle avec votre main, oui, en vous assurant de le faire verticalement. Méprisant la résistance à l'air, le mouvement qui suit la balle s'adapte parfaitement au modèle de mouvement rectiligne uniformément varié (MRUV).

Figure 1. Parler une balle verticalement est un bon exemple de tir vertical. Source: Pexels.

Le tir vertical est un mouvement largement étudié dans les cours d'introduction de la physique, car il s'agit d'un échantillon de la mouvement dans une dimension, Un modèle très simple et utile.

Ce modèle peut non seulement être utilisé pour étudier la cinématique des objets sous l'action de la gravité, mais aussi, comme nous le verrons plus tard, décrit le mouvement des particules au milieu d'un champ électrique uniforme.

[TOC]

Formules et équations

La première chose qui est nécessaire est un système de coordonnées pour indiquer l'origine et l'étiqueter avec une lettre qui, dans le cas des mouvements verticaux, est la lettre "et".

Ensuite, le sens positif est sélectionné +et, qui est généralement en place et le sens -et qui est généralement retiré (voir figure 2). Tout cela à moins que qui résout le problème décide le contraire, car une autre option consiste à prendre aussi positif la direction du mouvement, quel que soit.

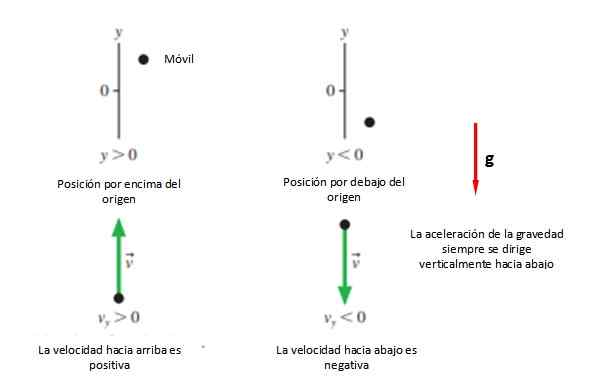Figure 2. Convention de signes habituelle dans la photo verticale. Source: F. Zapata.

Dans tous les cas, il est recommandé que l'origine coïncide avec le point de lancement et_soit, Parce que les équations sont simplifiées, bien que toute position souhaitée puisse être prise pour commencer à étudier le mouvement.

Il peut vous servir: deuxième condition d'équilibre: explication, exemples, exercices

Équations de prise de vue verticales

Une fois le système de coordonnées et l'origine établie, nous allons aux équations. Les amplitudes qui décrivent le mouvement sont:

-Vitesse initiale V_soit

-Accélération pour

-Vitesse V

-Position initiale X_soit

-Position X

-Déplacement DX

-Temps t

Tous sauf le temps sont des vecteurs, mais comme il s'agit d'un mouvement d'une seule dimension avec une certaine direction, qui compte alors utilise des signes de + ou - pour indiquer où l'ampleur en question est dirigée. Dans le cas du tir vertical, la gravité tombe toujours en panne et, sauf indication contraire, un panneau est attribué -.

Il y a alors les équations adaptées au tir vertical, en remplaçant "X" pour "et" et "pour" pour "g". De plus, le signe (-) correspondant à la gravité dirigée:

1) positionner: y = y_soit + V_soit.T - ½ g.t²

2) vitesse: V = V_soit - g.t

3) vitesse en fonction du déplacement Δet: V² = V_soit² - 2.g. Δet

Exemples

Ensuite, il y a des exemples d'application pour la prise de vue verticale. Dans sa résolution, ce qui suit doit être pris en compte:

-"g"Il a une valeur constante qui est en moyenne de 9,8 m / s² ou environ 10 m / s² Si il est préféré pour faciliter les calculs lorsqu'il n'est pas trop précis.

-Quand V_soit bien 0, Ces équations sont réduites à celles de chute libre.

-Si le lancement est en hausse, l'objet doit avoir une vitesse initiale qui vous permet de bouger. Une fois en mouvement, l'objet atteint une hauteur maximale qui dépendra de la taille de la vitesse initiale. Bien sûr, à une plus grande hauteur, le mobile passera plus de temps dans les airs.

-L'objet revient au point de départ avec la même vitesse avec laquelle il a été lancé, mais la vitesse est dirigée vers le bas.

-Pour un lancement vertical, plus la vitesse initiale est élevée, plus tôt l'objet arrivera au sol. Ici, la distance parcourue est fixée en fonction de la hauteur sélectionnée pour le lancement.

Peut vous servir: qu'est-ce que la rugosité relative et absolue?

-Dans la prise de vue verticale, le temps qui prend le mobile pour atteindre la hauteur maximale est calculé en faisant v = 0 Dans l'équation 2) de la section précédente. C'est lui temps maximum t_Max:

0 = V_soit - g . t_Max ⇒ t_Max = V_soit /g

-La hauteur maximale et_Max Il efface de l'équation 3) de la section précédente qui fait également v = 0:

0 = V_soit² - 2.g. Δy ⇒ 0 = V_soit² - 2.g. (et_Max - et_soit) ⇒ et_Max = Y_soit  + V_soit² / 2 g

Ouais et_soit = 0, Il est réduit à:

et_Max = V_soit² / 2 g

Exemple résolu 1

Une balle avec V est lancée verticalement vers le haut_soit = 14 m / s, du haut d'un bâtiment de 18 m de haut. Le ballon est autorisé à suivre son aval vers le trottoir. Calculer:

a) La hauteur maximale atteinte par le ballon par rapport au sol.

b) le temps dans l'air (temps de vol).

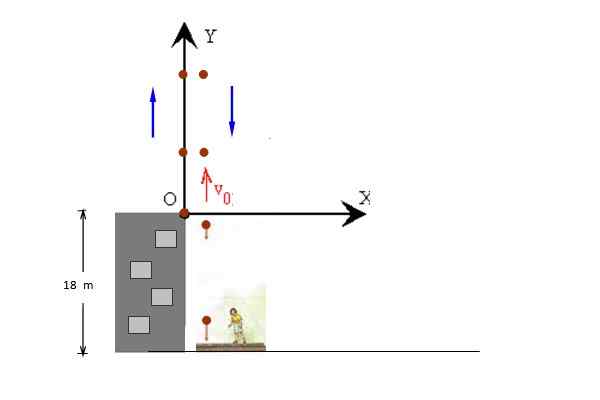figure 3. Une balle est lancée verticalement à partir du toit d'un bâtiment. Source: F. Zapata.

Solution

Dans la figure, les mouvements de montée et de baisse de la balle apparaissent séparément pour plus de clarté, mais les deux se produisent le long de la même ligne. La position initiale est prise à y = 0, de sorte que la position finale est y = - 18 m.

a) La mesure maximale mesurée du toit du bâtiment est et_Max = V_soit² / 2 g Et à partir de l'instruction, il est lu que la vitesse initiale est de +14 m / s, puis:

et_Max = (14 m / s)² / 2 x 9.8 m / s² = 10 m (Concernant le toit)

H_Max = 10 m + 18 m = 28 m (Concernant le trottoir).

b) pour trouver le Temps total soit temps de vol dure dans les airs, le ballon sera utilisé l'équation y = y_soit + V_soit.T - ½ g.t², Avec les valeurs et signes suivants:

y = - 18 m

et_soit = 0 m

V_soit = +14 m / s

Remplacement:

- 18 = 14.T - ½ 9.8 .t²

- 4.9 T²+14.T + 18 = 0 

4.9 T²-14.T - 18 = 0

Il s'agit d'une deuxième équation de degrés qui est facilement résolu à l'aide d'une calculatrice scientifique ou à l'aide de la résolution. Les solutions sont: 3.82 et -0.96. La solution négative est rejetée car c'est un temps manque de sens physique.

Il peut vous servir: chaleur: formules et unités, caractéristiques, comment elle est mesurée, exemples

Le temps de vol du ballon est 3.82 secondes.

Exemple résolu 2

Une particule chargée positivement Q = +1.2 MICICOULombs (MC) et masse m = 2.3 x 10 ^-dix Kg Il est projeté verticalement, à partir de la position indiquée sur la figure et avec une vitesse initiale V_soit = 30 km / s.

Parmi les plaques chargées, il y a un champ électrique ET uniforme, dirigé verticalement vers le bas et amplitude de 780 n / c. Si la distance entre les plaques est de 18 cm, la particule entrera-t-elle avec la plaque supérieure? Méprisez l'attraction gravitationnelle sur la particule, car elle est extrêmement légère.

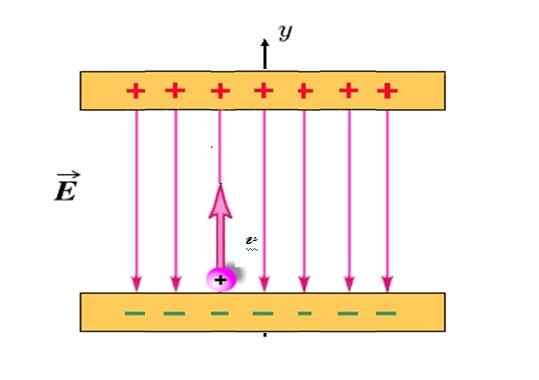Figure 4. Une particule de charge positive se déplace similaire à une balle lancée verticalement vers le haut, lorsqu'elle est immergée dans le champ électrique de la figure. Source: modifiée par f. Chaussure Wikimedia Commons.

Solution

Dans ce problème, le champ électrique ET est celui qui produit une force F et l'accélération qui en résulte. Étant chargé positivement, la particule est toujours attirée par la plaque inférieure, mais lorsqu'elle est projetée verticalement vers le haut, elle atteindra une hauteur maximale puis reviendra sur la plaque inférieure, comme la boule des exemples précédents.

Par définition du champ électrique:

E = f / q = m.A / Q ⇒ a = q.E / m

Il est nécessaire d'utiliser cette équivalence avant de remplacer les valeurs:

1 mc = 1 x 10^-3 C

Avec cela, l'accélération est:

A = 1.2 x 10^-3 X 780/2.3 x 10 ^-dixSP² = 4.07 x 10⁹ SP²

Pour la hauteur maximale, la formule de la section précédente est utilisée, mais au lieu d'utiliser "g"Cette valeur d'accélération est utilisée:

et_Max = V_soit² / 2a = (30.000 m / s)²/ 2 x 4.07 x 10⁹ SP² = 0.11 m = 11 cm

Ne collisez pas avec la plaque supérieure, car il est à 18 cm du point de départ, et la particule dès qu'elle soulève 11 cm.

https: // youtu.Be / kt08ntudzwq

Les références

1. Kirkpatrick, L. 2007. Physique: un regard sur le monde. 6^faire Édition abrégée. Cengage Learning. 23 - 27.
2. Rex, un. 2011. Fondamentaux de la physique. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14^e. Élégant. Volume 1. 50 - 53.
4. SERAY, R., Vulle, c. 2011. Fondamentaux de la physique. 9^{n / A} Élégant. Cengage Learning. 43 - 55.
5. Wilson, J. 2011. Physique 10. Pearson Education. 133 - 149.