Types de triangles

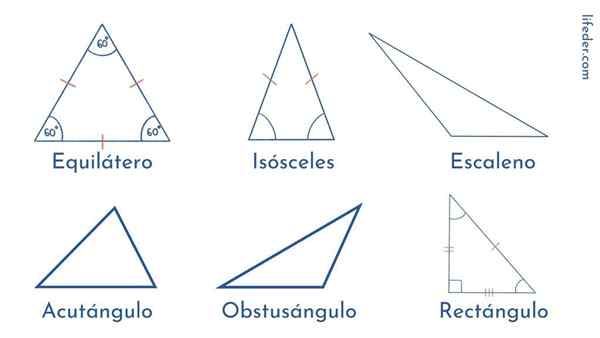Classification des triangles

Un triangle est un polygone ou une figure géométrique qui a trois côtés, trois sommets et trois angles. Les côtés sont chacune des lignes droites qui la forment. Les sommets sont les points où les côtés sont joints; Les angles sont les arcs ou les ouvertures qui se forment près des sommets, en rejoignant deux côtés.

Un triangle peut également être défini comme la zone déterminée par trois lignes. La somme de ses trois angles est toujours égale à 180º. La longueur de l'un de ses côtés est toujours inférieure au résultat de la somme de la longueur des deux autres côtés, mais supérieure à sa soustraction.

Les triangles sont les figures géométriques les plus simples et servent à étudier les propriétés mathématiques d'autres figures plus complexes, telles que les pentagones ou les hexagones.

Ils sont également utilisés dans d'autres sciences, comme la topographie, la navigation ou l'astronomie. Dans ce dernier, ils sont habitués à connaître la distance qui nous sépare d'un corps bleu clair éloigné de deux points d'observation situés sur Terre. Cette méthode est connue sous le nom de parallage.

Les triangles sont classés en fonction de la longueur de leurs côtés ou en fonction de l'amplitude de leurs angles.

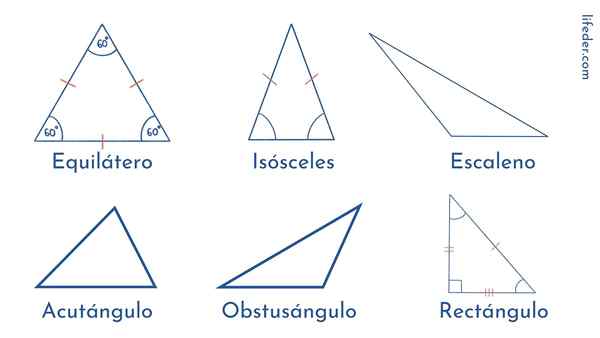
Types de triangles selon leurs côtés

Triangle équilatéral

Les côtés de ce type de triangle ont exactement la même longueur. Et il en va de même pour leurs angles: les trois mesurent 60º. C'est pourquoi nous disons que le triangle équilatéral est un polygone ordinaire.

Triangle scalène

Contrairement à l'équilatéral, dans le triangle scalène, tout est inégal: ses trois côtés ont des longueurs différentes et ses angles diffèrent en amplitude.

Peut vous servir: opérations combinées

Triangle isocèle

Dans ce type de triangle, nous constatons que les deux côtés ont la même mesure, tandis que le côté restant est différent. La même chose est observée dans l'amplitude des angles: deux sont les mêmes et un.

Types de triangles selon leurs angles

Triangle rectangle

Il se caractérise par un angle droit, c'est-à-dire 90º. Ses deux autres angles sont aigus ou moins de 90º.

Dans ce type de triangles, le côté le plus long est appelé Hypotenusa, tandis que deux autres côtés sont les catégories.

Triangle oblique

Les triangles qui n'ont pas d'angle droit appartiennent à ce type. Ils sont subdivisés en deux types:

Triangle Acutangle: Ses trois angles sont aigus.

Triangle obtus: Ils ont deux angles aigus et un obtus ou supérieur à 90º.

Triangles mixtes

Le même triangle peut être classé selon les deux critères, c'est-à-dire, selon la longueur de leurs côtés et l'amplitude de leurs angles.

Par exemple, un triangle rectangle peut également être Escalano ou Isoscéles, mais il ne pourrait pas être équilatéral, car ce dernier ne présente aucun angle droit.

Cependant, un triangle équilatéral pourrait être aigu, car il a effectivement trois angles aigus ou moins de 90 °.

Triangle de scalène obtus

Un triangle scalène peut être obtuctement, car à la fois l'amplitude de ses angles et la longueur de ses côtés sont différentes.

Comment calculer le périmètre d'un triangle?

Le produit de la somme de la longueur des trois côtés d'un triangle est appelé périmètre.

Regardons quelques exemples.

1- On nous demande de trouver le périmètre d'un triangle scalène dont les côtés 6, 8 et 4 centimètres. Tout ce que nous avons à faire est d'ajouter:

Peut vous servir: constante absolue

6 + 8 + 4 = 18

Par conséquent, le périmètre de ce triangle scalène est de 10 centimètres.

2- Ensuite, ils nous demandent de calculer le périmètre d'un triangle isocèle dont les côtés mesurent 4 centimètres les deux et 6 centimètres le côté restant. Étant donné que deux de ses côtés ont la même longueur, nous devons placer le même chiffre deux fois, comme ceci:

4 + 4 + 6 = 14

Le périmètre de ce triangle est de 14 centimètres.

3- Un dernier exemple. Nous avons la tâche de déterminer le périmètre d'un triangle équilatéral de 9 centimètres latéralement. Comme nous connaissons les caractéristiques des différents types de triangles, nous savons que l'équilatéral se distingue parce que ses trois côtés sont égaux. Donc:

9 + 9 + 9 = 27

Le périmètre de cet équilatéral est de 27 centimètres.

MediaTrices, bissecteurs et médium

Ce sont les trois types de lignes droites qui peuvent être dessinées dans un triangle.

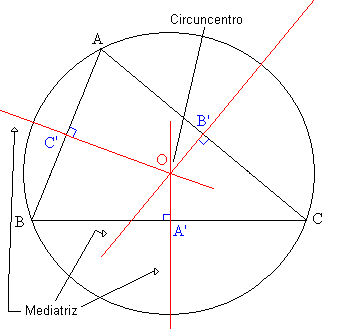
Médiatrices

Il y en a trois, un de chaque côté du triangle. Le MediaTrix est une ligne droite qui passe par le milieu du côté triangle auquel il correspond. Les trois méditrices d'un triangle se croisent à un point connu sous le nom de circoncentro, qui est à la même distance de chacun des sommets du triangle.

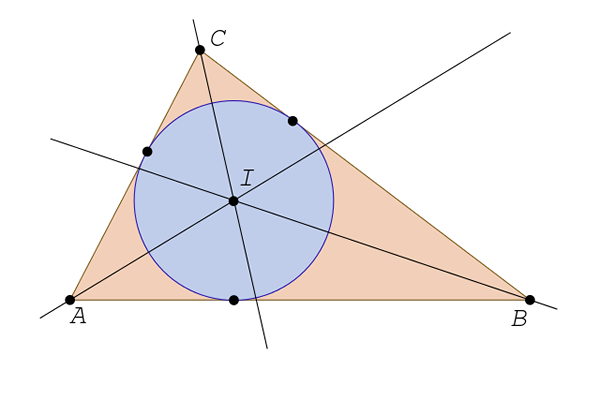
Bissecteur

Il y en a trois, un pour chaque angle. La bissectrice est une ligne droite qui commence du sommet et divise l'angle en deux parties égales. Les bissecteurs d'un triangle se croisent à un point connu sous le nom d'intestin.

Moyen

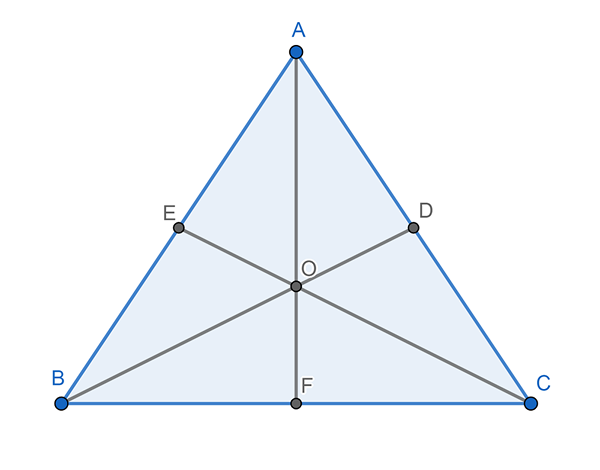
Il y en a aussi trois, un pour chaque sommet. Une médiane est une ligne qui commence à partir d'un sommet et atteint le point médian du côté opposé. Les médianes d'un triangle se croisent à un point appelé baricentro.

Peut vous servir: Erreur d'échantillonnage: formules et équations, calcul, exemples

La distance entre l'un des trois sommets et le barycenter équivaut à deux tiers (2/3) de la longueur totale de la médiane correspondante. Par exemple, si le CE médian mesure 5 centimètres, alors la distance entre C et le barcentrique (O) est égale 5 x 2/3, ou ce qui est le même, 5 x 0,66, ce qui se traduit par 3, 3 centimètres.

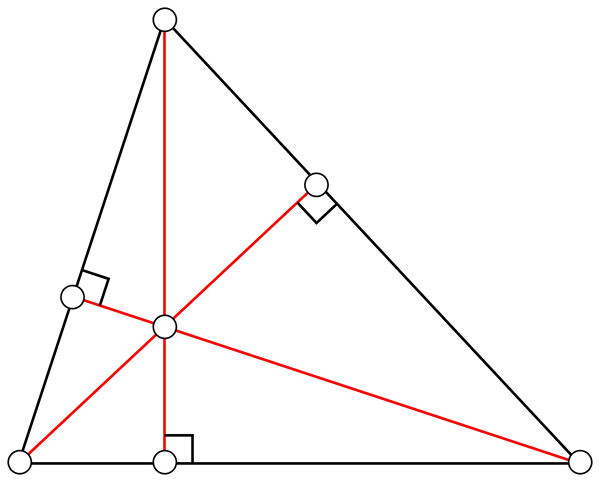
hauteurs

C'est une ligne droite qui rejoint un sommet avec le côté opposé. Les trois hauteurs d'un triangle se croisent à un point appelé Ortotroenter. Selon le type de triangle, l'orthocentre peut être à l'intérieur ou à l'extérieur de la zone du triangle.

Comment calculer la zone du triangle?

La zone d'un triangle de toute nature peut être connue lors de l'application de la formule suivante:

A = b x h / 2

Dans cette équation, A fait référence à la zone; B fait référence à la base et h est la hauteur.

Regardons un exemple. On nous demande de calculer la zone d'un triangle dont la base mesure 12 centimètres et dont la hauteur est de 7 centimètres. Ainsi, nous avons:

B = 12

H = 7

Nous appliquons la formule:

A = 12 x 7/2

A = 84/2

A = 44

Ce triangle a donc une superficie de 44 centimètres carrés.