Types d'intégrales
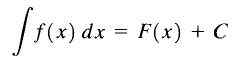
- 4453
- 208
- Eva Henry
Les Types d'intégrales que nous sommes dans le calcul sont les intégrales indéfinies et les intégrales définies. Bien que les intégrales définies aient beaucoup plus d'applications que les intégrales indéfinies, il est d'abord nécessaire d'apprendre à résoudre les intégrales indéfinies.
L'une des applications les plus attrayantes des intégrales définies est le calcul du volume d'un solide de révolution. Les deux types d'intégrales ont les mêmes propriétés de linéarité et les techniques d'intégration ne dépendent pas du type d'intégrale.
Mais en dépit d'être très similaire, il y a une différence principale; Dans le premier type d'intégrale, le résultat est une fonction (qui n'est pas spécifique) tandis que dans le deuxième type, le résultat est un nombre.
Types de base des intégrales
Le monde des intégrales est très large, mais en cela, nous pouvons distinguer deux types de base d'intégrales, qui ont une grande applicabilité dans la vie quotidienne.
1- intégrales indéfinies
Si f '(x) = f (x) pour tous les x dans le domaine de f, nous disons que F (x) est un antidérivatif, une primitive ou une intégrale de f (x).
D'un autre côté, remarquez que (f (x) + c) '= f' (x) = f (x), ce qui implique que l'intégrale d'une fonction n'est pas unique, car il donne des valeurs différentes à la constante C Nous obtiendrons différents antidérivatifs.
Pour cette raison, F (x) + C est appelé l'intégrale indéfinie de F (x) et C est appelée constante d'intégration et nous l'écrivons comme suit:
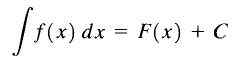 Intégral indéfini
Intégral indéfini Comme nous pouvons le voir, l'intégrale indéfinie de la fonction f (x) est une famille de fonctions.
Par exemple, si vous souhaitez calculer l'intégrale indéfinie de la fonction F (x) = 3x², d'abord un antidérivatif de f (x) doit être trouvé en premier.
Peut vous servir: trinomialIl est facile de noter que f (x) = x³ est un antidérivatif, puisque f '(x) = 3x². Par conséquent, on peut conclure que
∫f (x) dx = ∫3x²dx = x³ + c.
2- INTÉGRALES définies
Soit y = f (x) une fonction réelle se poursuit dans un intervalle fermé [a, b] et être f (x) un antidérivatif de f (x). Il est appelé l'intégrale définie de f (x) entre les limites a et b au nombre F (b) -f (a), et indique comme suit:
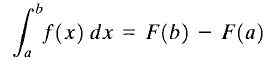 Théorème de calcul fondamental
Théorème de calcul fondamental La formule illustrée ci-dessus est mieux connue comme "le théorème fondamental du calcul". Ici "A" est appelé la limite inférieure et "B" est appelé Limite supérieure. Comme on peut le voir, l'intégrale définie d'une fonction est un nombre.
Dans ce cas, si l'intégrale définie de f (x) = 3x² est calculée dans l'intervalle [0,3], un nombre sera obtenu.
Pour déterminer ce nombre, nous choisissons f (x) = x³ comme antidérivatif de f (x) = 3x². Ensuite, nous calculons f (3) -f (0) qui nous lance en conséquence 27-0 = 27. En conclusion, l'intégrale définie de f (x) dans l'intervalle [0,3] est 27.
On peut noter que si g (x) = x³ + 3, alors g (x) est choisi, est un antidérivatif de f (x) différent de f (x), mais cela n'affecte pas le résultat comme g (3) -g (0) = (27 + 3) - (3) = 27. Pour cette raison, dans les intégrales définies, la constante d'intégration n'apparaît pas.
L'une des applications les plus utiles de ce type d'intégrale est qu'elle permet de calculer la zone (volume) d'une figure plate (d'une révolution solide), établissant des fonctions et limites d'intégration adéquates (et un axe de rotation).
Parmi les intégrales définies, nous pouvons trouver diverses extensions de celle-ci, telles que les lignes intégrales, les intégrales de surface, les intégrales inappropriées, les intégrales multiples, entre autres, toutes avec des applications très utiles en science et ingénierie.
Il peut vous servir: différence entre cercle et circonférence (avec des exemples)Les références
- Kishan, H. (2005). Calcul intégral. Éditeurs et distributeurs de l'Atlantique.
- Purcell, E. J., Varberg, D., & Rigdon, s. ET. (2007). Calcul (Ninth Ed.). Prentice Hall.

