Théorème binomial

Quel est le théorème binomial?

Il théorème binomial C'est une équation qui nous dit comment se développe une expression de la forme (A + B)ⁿ Pour un nombre naturel n. Un binôme n'est rien de plus que la somme de deux éléments, comme (a + b). Il nous permet également de savoir pour un terme donné par^kb^N-k Quel est le coefficient qui l'accompagne.

Ce théorème est généralement attribué à l'inventeur anglais, physique et mathématicien Sir Isaac Newton; Cependant, divers enregistrements ont été constatés qui indiquent que son existence était déjà connue au Moyen-Orient, vers l'an 1000.

Numéros combinatoires

Le théorème binomial nous dit mathématiquement ce qui suit:

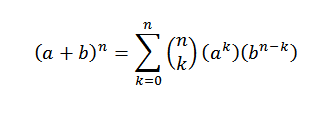
Dans cette expression, A et B sont des nombres réels et n est un nombre naturel.

Avant de donner la démonstration, voyons quelques concepts de base nécessaires.

Le nombre combinatoire ou les combinaisons de n en k est exprimé comme suit:

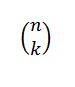
Cela exprime la valeur du nombre de sous-ensembles avec des éléments k peuvent être choisis parmi un ensemble de n éléments. Son expression algébrique est donnée par:

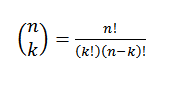
Regardons un exemple: Supposons que nous ayons un groupe de sept balles, dont deux sont rouges et les autres sont bleus.

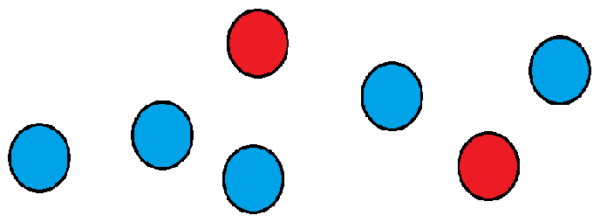
Nous voulons savoir combien de façons nous pouvons les commander dans une rangée. Une façon pourrait être de placer les deux rouges en première et deuxième position, et le reste des balles dans les positions qui restent.

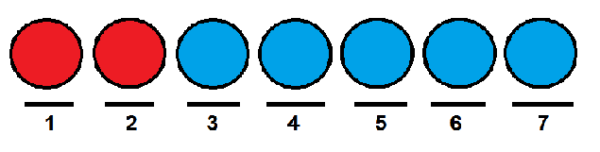
Semblable au cas précédent, nous pourrions donner aux balles rouges la première et dernière position respectivement, et occuper les autres avec des boules bleues.

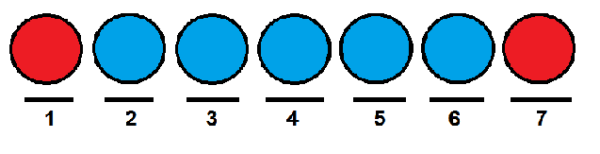
Maintenant, un moyen efficace de compter le nombre de façons dont nous pouvons commander les balles d'affilée est d'utiliser des nombres combinatoires. Nous pouvons voir chaque position comme un élément de l'ensemble suivant:

Peut vous servir: nombres parfaits: comment les identifier et les exemples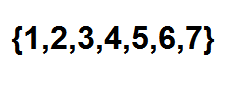

Vous trouverez ci-dessous seulement pour choisir un sous-ensemble de deux éléments, dans lequel chacun de ces éléments représente la position que les boules rouges occupent. Nous pouvons faire ce choix selon la relation donnée par:

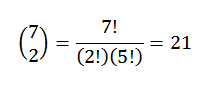
De cette façon, nous avons qu'il existe 21 façons de commander de telles balles.

L'idée générale de cet exemple sera très utile dans la démonstration du théorème binomial. Regardons un cas particulier: si n = 4, nous avons (a + b)⁴, Ce n'est rien de plus que:

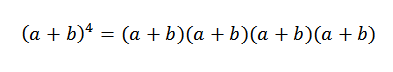
Lorsque nous développons ce produit, nous avons la somme des termes obtenus en multipliant un élément de chacun des quatre facteurs (A + B). Ainsi, nous aurons des termes qui seront en forme:

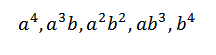
Si nous voulions obtenir le terme du formulaire pour⁴, Il suffit de se multiplier comme suit:

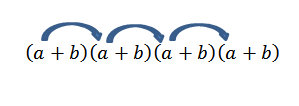
Notez qu'il n'y a qu'une seule façon d'obtenir cet élément; Mais que se passe-t-il si nous recherchons maintenant la fin du formulaire²b²? Comme "A" et "B" sont des nombres réels et, par conséquent, cela vaut la loi commutative, nous devons obtenir ce terme est de se multiplier avec les membres comme indiqué par les flèches.

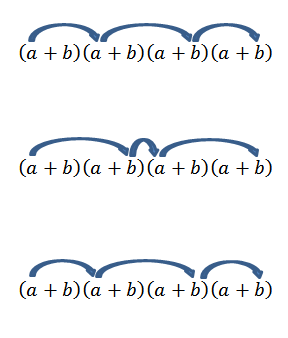
Effectuer toutes ces opérations est généralement quelque peu fastidieux, mais si nous voyons le terme "A" comme une combinaison où nous voulons savoir combien de façons nous pouvons choisir deux "A" dans un ensemble de quatre facteurs, nous pouvons utiliser l'idée de L'exemple précédent de l'exemple précédent. Nous avons donc ce qui suit:

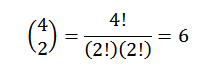
Ainsi, nous savons que dans le développement final de l'expression (A + B)⁴ Nous aurons exactement 6ème²b². En utilisant la même idée pour d'autres éléments, vous devez:

Peut vous servir: Nombres transcendants: quelles sont les formules, les exemples, les exercices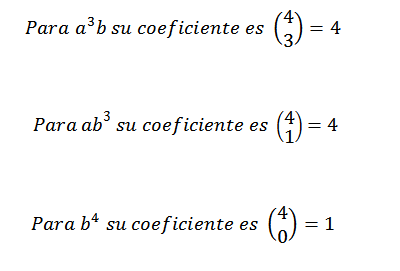

Ensuite, nous ajoutons les expressions obtenues ci-dessus et nous devons:

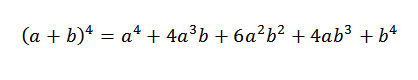
C'est une démonstration formelle pour le cas général dans lequel "n" est un numéro naturel.

Manifestation

Notez que les termes restaient lors du développement (A + B)ⁿ Ils sont de la forme à^kb^N-k, où k = 0,1,…, n. En utilisant l'idée de l'exemple précédent, nous avons le moyen de choisir des variables "k", un "des facteurs" n "est:

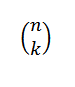
Lors du choix de cette manière, nous choisissons automatiquement les variables N-K "B". Cela suit cela:

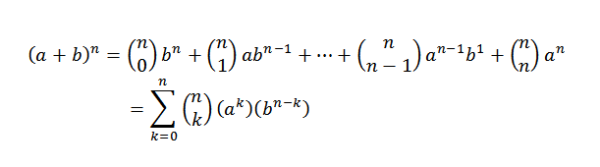
Exemples

Considérant (A + B)⁵, Quel serait votre développement?

Pour le théorème binomial, nous devons:

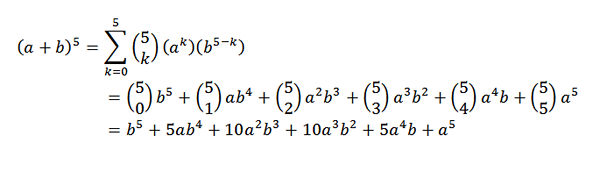
Le théorème binomial est très utile si nous avons une expression dans laquelle nous voulons savoir quel est le coefficient d'un terme spécifique sans avoir à effectuer le développement complet. Par exemple, nous pouvons prendre l'inconnu suivant: quel est le coefficient x⁷et⁹ Dans le développement de (x + y)¹⁶?

Pour le théorème binomial, nous avons que le coefficient est:

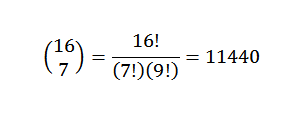
Un autre exemple serait: quel est le coefficient x⁵et⁸ Dans le développement de (3x-7y)¹³?

Nous réécrivons d'abord l'expression d'une manière pratique; c'est:

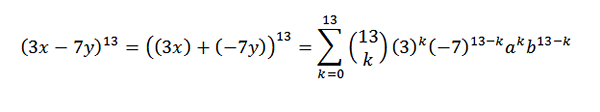
Ensuite, en utilisant le théorème binomial, nous avons que le coefficient recherché est lorsque vous avez k = 5

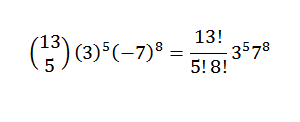
Un autre exemple des utilisations de ce théorème est la démonstration de certaines identités communes, comme celles que nous mentionnerons ci-dessous.

Identité 1

Si "n" est un nombre naturel, nous devons:

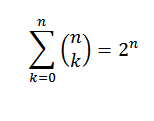
Pour la démonstration, nous utilisons le théorème binomial, où "A" et "B" prennent la valeur de 1. Ensuite nous avons:

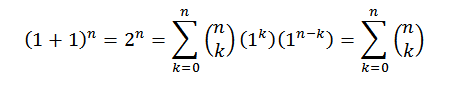
De cette façon, nous avons prouvé la première identité.

Peut vous servir: sélections aléatoires avec ou sans remplacement

Identité 2

Si "n" est un nombre naturel, alors

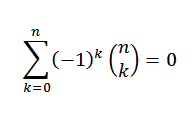
Pour le théorème binomial, nous devons:

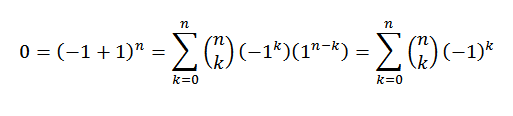
Une autre démonstration

Nous pouvons faire une démonstration différente pour le théorème binomial en utilisant la méthode inductive et l'identité de Pascal, qui nous dit que, si "n" et "k" sont des entiers positifs qui rencontrent n ≥ k, alors:

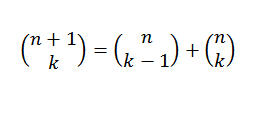
Démonstration d'induction

Voyons que la base inductive est remplie.  Si n = 1, nous devons:

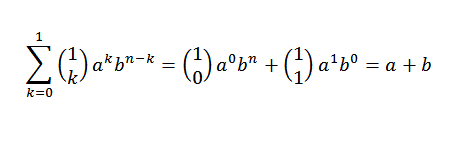
En effet, nous voyons qu'il est accompli. Maintenant, soit n = j tel qu'il est accompli:

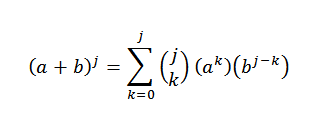
Nous voulons voir que pour n = j + 1, il est vrai que:

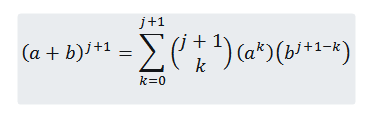
Nous devons donc:

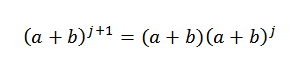
Par hypothèse, nous savons que:

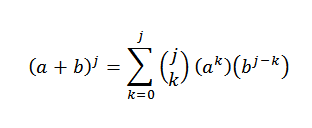
Ensuite, en utilisant une propriété distributive:

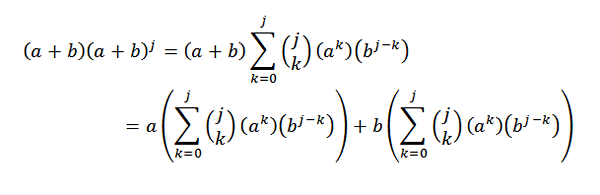
Par la suite, le développement de chacun des résumés est:

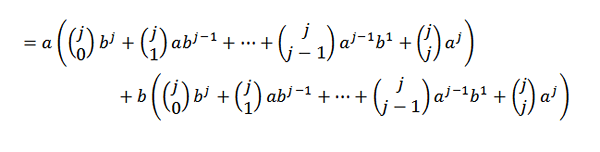
Maintenant, si nous nous regroupons commodément, nous devons:

En utilisant l'identité de Pascal, nous devons:

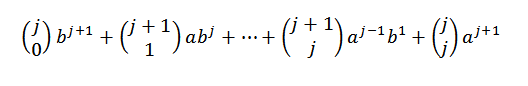
Enfin, notez que:

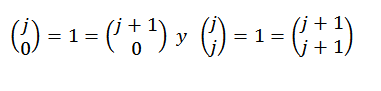
Par conséquent, nous voyons que le théorème binomial est réalisé pour chaque "n" appartenant à des nombres naturels, et avec cela, le test se termine.

Curiosités

Le nombre combinatoire (NK) est également appelé coefficient binomial car c'est précisément le coefficient qui apparaît dans le développement du binomial (A + B)ⁿ.

Isaac Newton a donné une généralisation de ce théorème pour le cas dans lequel l'exposant est un nombre réel; Ce théorème est connu sous le nom de théorème binomial de Newton.

Déjà dans l'antiquité, ce résultat était connu pour le cas particulier dans lequel n = 2. Cette affaire est mentionnée dans le Articles d'Euclide.