Théorème d'explication Steiner, applications, exercices

Il Théorème de Steiner, Aussi connu comme Théorème de l'axe parallèle, Il permet d'évaluer le moment d'inertie d'un corps étendu, autour d'un axe parallèle à un autre qui passe à travers le centre de la masse de l'objet.

Il a été découvert par le mathématique suisse_Cm Le moment d'inertie de l'objet par rapport à un axe qui passe par son centre de masse CM et I_z le moment de l'inertie par rapport à un autre axe parallèle à cela.

Figure 1. Une porte rectangulaire allumant ses joies a un moment d'inertie qui peut être calculée en appliquant le théorème de Steiner. Source: Pixabay.

Connu de la distance D qui sépare les deux axes et la masse M du corps en question, le moment d'inertie par rapport à l'axe incognito est:

Toi_z = I_Cm + MARYLAND²

Le moment d'inertie indique à quel point il est facile pour un objet de tourner autour d'un certain axe. Cela dépend non seulement du corps du corps, mais de la façon dont il est distribué. Pour cette raison, il est également connu comme Inertie de rotation, Être vos unités dans le système international KG . m².

Le théorème montre que le moment de l'inertie Toi_z C'est toujours plus grand que le moment de l'inertie Toi_Cm en un montant donné par M.D².

[TOC]

Applications

Comme un objet est capable de tourner autour de nombreux axes, et dans les tableaux généralement uniquement le moment d'inertie concernant l'axe qui passe par le centroïde, le théorème de Steiner facilite le calcul lorsqu'il doit faire tourner les corps sur des essieux sur des essieux qui ne coïncident pas avec ce.

Peut vous servir: mouvement rectiligne: caractéristiques, types et exemples

Par exemple, une porte ne tourne généralement pas autour d'un axe qui passe par son centre de masse, mais en ce qui concerne un axe latéral, où les charnières adhèrent.

Lorsque vous connaissez le moment de l'inertie, il est possible de calculer l'énergie cinétique associée à la rotation sur cet axe. Ouais K est l'énergie cinétique, Toi le moment d'inertie autour de l'axe en question et Ω La vitesse angulaire est réalisée que:

K = ½ i.Ω²

Cette équation est très similaire à la formule très familière de l'énergie cinétique pour un objet de masse M se déplaçant à vitesse V:  K = ½ m.V². Et c'est le moment d'inertie ou d'inertie rotationnelle Toi joue en rotation le même rôle que la pâte M Dans la traduction.

Démonstration du théorème de Steiner

Le moment d'inertie d'un objet étendu est défini comme:

I = ∫r² DM

Où DM C'est une masse de masse infinitésimale et r C'est la distance entre DM et l'axe de rotation z. Dans la figure 2, cet axe traverse le centre de masse CM, mais il peut s'agir de n'importe qui.

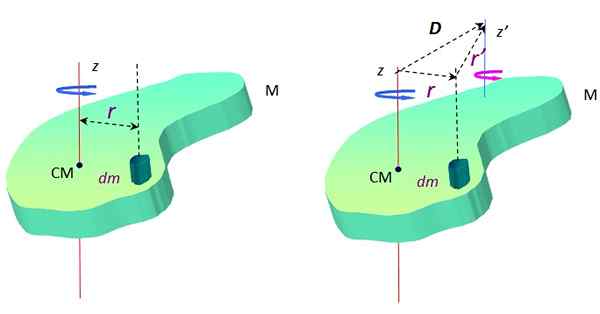Figure 2. Un objet étendu en rotation autour de deux axes parallèles. Source: F. Zapata.

Autour d'un autre axe  z ', Le moment de l'inertie est:

Toi_z= ∫ (R ')² DM

Maintenant, selon le triangle formé par les vecteurs D, r et R ' (Voir la figure 2 à droite), il y a une somme vectorielle:

r + R ' = D   → R ' = D - r

Les trois vecteurs sont sur le plan de l'objet qui peut être le Xy. L'origine du système de coordonnées (0,0) est choisie en CM pour faciliter les calculs qui suivent.

De cette façon, le module carré du vecteur R ' est:

Peut vous servir: Biophysique: Histoire, quelles études, applications, concepts, méthodes

(R ')² = (D_X- r_X)² +(D_et - r_et)² =

= D_X² + D_et² +r_X² + r_et2 -2d_Xr_X - 2 D_etr_et =

= D² + r²  - 2d_Xr_X - 2 D_etr_et

Maintenant, ce développement est remplacé dans l'intégrale du moment de l'inertie i_z et aussi la définition de la densité dm = ρ est utilisée.DV:

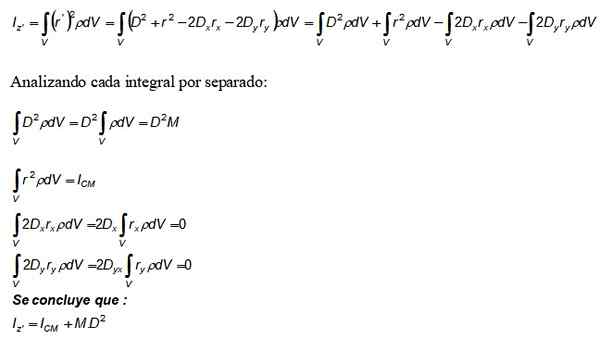
Le terme m. D² qui apparaît dans le théorème de Steiner provient de la première intégrale, la seconde est le moment d'inertie concernant l'axe qui passe par CM.

Pour sa part, les troisième et quatrième intégrales valent 0, car par définition, elles constituent la position du CM, qui a été choisie comme origine du système de coordonnées (0,0).

Exercices résolus

-Exercice résolu 1

La porte rectangulaire de la figure 1 a une masse de 23 kg, 1,30 de large et 2,10 m de haut. Déterminez le moment d'inertie de la porte concernant l'axe qui passe par la joie, en supposant que la porte est mince et uniforme.

figure 3. Schéma pour l'exemple résolu 1. Source: Pixabay modifié.

Solution

À partir d'une table des moments d'inertie, pour une plaque rectangulaire de masse m et dimensions pour et b, Le moment d'inertie par rapport à l'axe qui passe par son centre de masse est: i_Cm = (1/12)M(pour² + b²).

Une porte homogène sera supposée (une approche, car la porte de la figure n'est probablement pas tant). Dans ce cas, le centre de masse passe par son centre géométrique. Dans la figure 3, un axe qui passe à travers le centre de masse a été dessiné et qui est également parallèle à l'axe qui passe à travers la joie.

Toi_Cm = (1/12) x 23 kg x (1.30²+2.dix²) m² = 11.7 kg.m²

Peut vous servir: qu'est-ce qu'un géoïde?

Appliquer le théorème de Steiner pour l'axe de rotation verte:

I = i_Cm + MARYLAND² = 11.7 kg.m² + 23 kg x 0.652 m² = 21.4 kg.

-Exercice résolu 2

Trouvez le moment d'inertie d'une fine tige homogène lorsqu'elle tourne par rapport à un axe qui passe par l'une de ses extrémités, voir la figure. Est-ce plus ou inférieur au moment de l'inertie quand il tourne autour de son centre? Parce que?

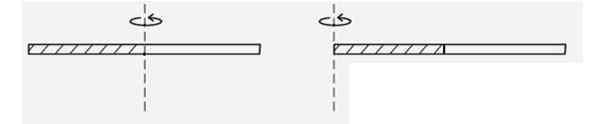Figure 4. Schéma pour l'exemple résolu 2. Source: F. Zapata.

Solution

Selon les moments d'inertie, le moment de l'inertie Toi_Cm d'une fine tige de pâte M et longueur L est: Toi_Cm = (1/12) ml²

Et le théorème de Steiner déclare que lorsqu'il est tourné autour d'un axe qui passe à travers une extrémité D = L / 2 reste:

I = i_Cm + MARYLAND² = (1/12) ml² + M (l / 2)² = (1/3) ml²

C'est vieux.

L'influence de la distance à l'axe de rotation n'est pas linéaire, mais quadratique. Une masse qui représente le double de la distance qu'un autre aura un moment d'inertie proportionnel à (2d)² = 4d².

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill. 313-340.
2. Georgia State University. Mouvement rotatif. Récupéré de: Phys.Nthu.Édu.Tw.
3. Théorème de l'axe parallèle. Récupéré de: hyperphysique.Phy-asch.GSU.Édu.
4. Rex, un. 2011. Fondamentaux de la physique. Pearson. 190-200.
5. Wikipédia. Théorème de l'axe parallèle. Récupéré de: dans.Wikipédia.org