Somme de la méthode graphique des vecteurs, exemples, exercices résolus

La somme des vecteurs C'est l'opération d'addition entre les vecteurs qui se traduit par un autre vecteur. Les vecteurs sont caractérisés par l'ampleur, ainsi que la direction et le sens. Par conséquent, il n'est pas possible, en général, de les ajouter comme cela serait fait avec des quantités scalaires, c'est-à-dire en ajoutant des nombres.

Le vecteur obtenu à partir de la somme de plusieurs vecteurs est appelé vecteur résultant. En mécanique, nous parlons du force résultante, qui est la somme vectorielle de toutes les forces sur un corps. Ce résultat équivaut à l'ensemble ou au système de forces.

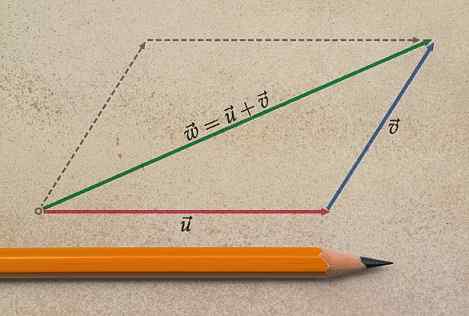
Pour spécifier complètement le vecteur de somme, il est nécessaire d'indiquer l'ampleur et l'unité, la direction et le sens.

Il est important de souligner qu'en ajoutant des vecteurs, ceux-ci doivent représenter la même ampleur physique, donc la somme vectorielle est une opération homogène. Cela signifie que nous pouvons ajouter une force avec une autre, mais pas une force avec un déplacement, car le résultat est dénué de sens.

Plusieurs méthodes sont disponibles pour trouver le vecteur résultant: graphiques et analyses. Pour trouver des sommes vectorielles avec des méthodes graphiques, il est basé sur une représentation simple pour un vecteur, à savoir une flèche ou une flèche de segment:

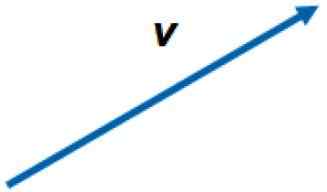Représentation graphique d'un vecteur dans le plan. Source: F. Zapata.

Les vecteurs sont désignés par des lettres noires dans du texte imprimé, ou avec une flèche sur la lettre, pour les distinguer de leurs amplitudes respectives ou des quantités scalaires. Par exemple, l'ampleur du vecteur V C'est simplement V.

[TOC]

Méthode graphique pour ajouter des vecteurs

Pour ajouter plus de deux vecteurs de couple, le Méthode de polygone soit polygone, qui consiste à se transférer à chacun des vecteurs adressés. Une caractéristique des vecteurs est qu'ils sont invariants concernant la traduction, nous utiliserons donc cette propriété pour établir la somme.

Peut vous servir: dilatation thermique

Il commence par l'un des vecteurs, car l'ajout de vecteur est commutatif et l'ordre des ajouts ne modifie pas la somme. Le deuxième vecteur se déplace ci-dessous, correspondant à son origine avec la fin du premier.

Ensuite, il est amené au vecteur suivant, puis met la même procédure, qui est pour correspondre à l'origine avec la fin de la précédente. Nous procédons de cette manière pour positionner le dernier vecteur.

Le vecteur résultant est celui qui rejoint l'origine du premier avec la fin libre du dernier. Le nom de cette méthode vient de la figure qui en résulte: un polygone.

Exemple

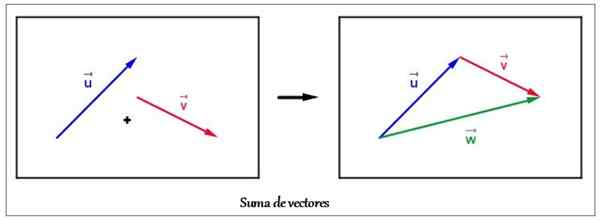
Exemple de somme de deux vecteurs dans le plan par la méthode graphique. Source: Wikimedia Commons

Prenons comme exemple la somme de deux vecteurs ou et V qui est illustré dans la figure supérieure.

En commençant par le vecteur ou, Il a déménagé au vecteur V Pour correspondre à son origine avec la fin du premier. Le vecteur résultant W Il est tiré de l'origine de ou à la fin de V, Former une figure à trois côtés: un triangle. C'est pourquoi dans ce cas particulier, la procédure est appelée Méthode de triangle.

Remarque un détail important, l'ampleur ou le module du vecteur résultant n'est pas la somme des modules des vecteurs supplémentaires. En fait, c'est presque toujours moins, à moins que les vecteurs ne soient parallèles.

Voyons ci-dessous ce qui se passe dans ce cas.

Cas spécial: somme des vecteurs parallèles

La méthode décrite peut également être appliquée au cas spécial dans lequel les vecteurs sont parallèles. Considérez l'exemple suivant:

Peut vous servir: Boltzmann constant: histoire, équations, calcul, exercicesSomme des vecteurs parallèles. Source: F. Zapata.

Le vecteur est laissé V Dans sa position d'origine, et se déplace vers le vecteur ou de telle manière que son origine est d'accord avec la fin de  V. Maintenant, un vecteur est tiré de l'origine de V Et la fin de ou.

C'est le vecteur résultant W Et sa taille est la somme des tailles des annonces. La direction et la direction des trois vecteurs sont les mêmes.

Le vecteur résultant a un module maximal si les addateurs forment un angle de 0º, comme ceux de l'exemple. Si les vecteurs forment un angle de 180º les uns avec les autres, alors le vecteur résultant a un module minimum.

Exemples de somme de vecteurs

- Déplacements

Un cycliste parcourt les premiers 3 km en direction du nord, puis 4 km à l'ouest. Votre déplacement, que nous appelons R, Il se trouve facilement avec la méthode Triangle plus un système de référence, où les points cardinaux sont marqués:

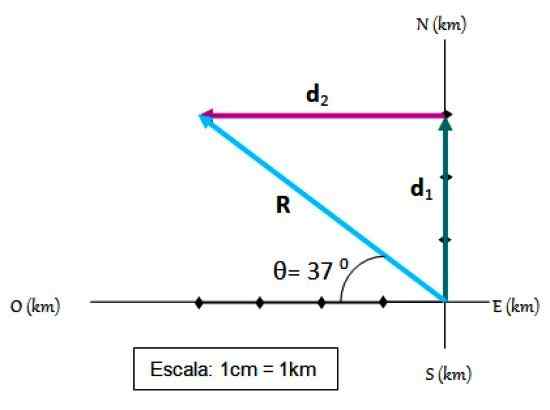Résultant de deux déplacements. Source: F. Zapata.

Étapes pour ajouter un vecteur

-Le point de départ coïncide avec l'origine du système de référence.

-Sur les axes de coordonnées, une échelle est choisie, ce qui dans ce cas est 1 cm = 1 km

-Le premier déplacement est dessiné à l'échelle d_1.

-Puis un d₁ Le deuxième déplacement est dessiné d₂, Également à l'échelle.

-Le déplacement résultant R C'est un vecteur qui passe de l'origine à la fin de d₂.

-La taille de R Il est mesuré avec une règle graduée, il est facile de vérifier que r = 5.

-Enfin l'angle qui R La forme avec l'horizontal est mesurée à l'aide d'un transporteur et se révèle être θ = 37 ⁰

- Vitesse qui en résulte

Un nageur veut traverser une rivière et pour cela rien à une vitesse de 6 km / h, perpendiculaire au rivage, mais un courant qui transporte une vitesse de 4 km / h le déviation.

Il peut vous servir: ohm: mesures de résistance, exemples et exercice résolus

Pour connaître sa vitesse résultante, les vecteurs de vitesse du nageur sont ajoutés, qui ont été dessinés verticaux et courant, qui est horizontal.

Suivant la méthode graphique, la vitesse résultante est obtenue V_R:

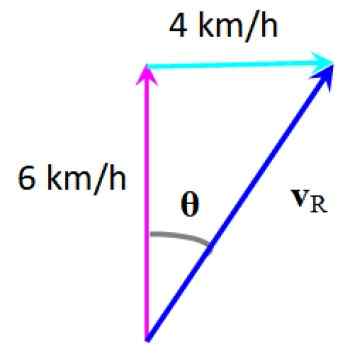Vitesse qui en résulte. Source: F. Zapata.

L'écart subi par le nageur peut être calculé par:

θ = arctg (4/6) = 33.7e à droite de votre adresse initiale

L'ampleur de sa vitesse augmente car la vitesse de la rivière ajoute vectorielle. Vous pouvez trouver une échelle soigneusement, comme dans l'exemple précédent.

Ou avec l'aide des raisons trigonométriques de 33.7e:

Sen 33.7e = 4 / V_R

V_R = 4 / sin 33.7e = 7.21 km / h

Exercice résolu

Sur une particule, la loi sur les forces suivantes, dont les amplitudes sont énumérées ci-dessous:

F₁= 2.5 N; F₂= 3 n; F₃= 4 n; F₄= 2.5 N

Trouvez la force résultante.

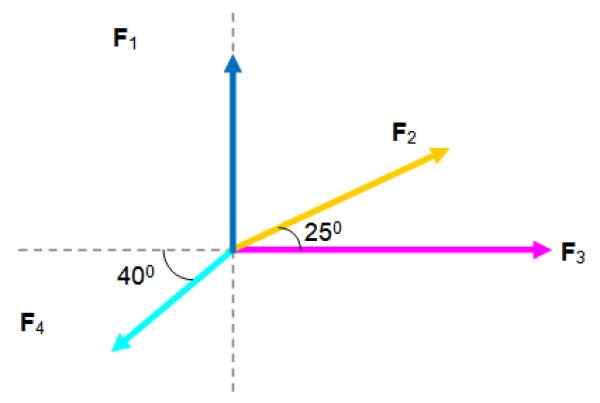Système de forces coplanaires. Source: F. Zapata.

Solution

Nous pouvons ajouter graphiquement à commencer par l'un des vecteurs, car la somme vectorielle est commutative.

Dans la figure, A a commencé avec F₁. Établir une échelle et avec l'aide de la règle et de l'équipe, les autres vecteurs sont transférés pour les placer l'un après l'autre.

Le vecteur F_R est dirigé de l'origine de F₁ à la fin de F₄. Son ampleur est 5.2 n et forme un angle de 26.5e par rapport à l'horizontal.

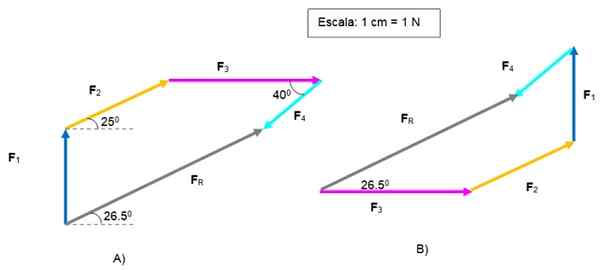Somme graphique vectorielle. Source: F. Zapata.

Dans la figure B, le même problème a été résolu, à commencer par F₃ et se terminant avec F₄, Pour obtenir la même chose F_R .

Les polygones sont différents, mais le résultat est le même. Le lecteur peut tester à nouveau l'ordre des vecteurs.

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
2. Bedford, 2000. POUR. Mécanique pour l'ingénierie: statique. Addison Wesley.
3. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 1. Cinématique. Édité par Douglas Figueroa (USB).
4. Giambattista, un. 2010. La physique. 2e. Élégant. McGraw Hill.
5. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. Volume 1.