Ce sont les segments rectilinéaires qui sont possibles dans chaque polygone

La diagonale d'un carré

Les segments rectilinéaires qui sont possibles dans chaque polygone sont les diagonales. Une diagonale est un segment de ligne qui est dessiné en rejoignant deux sommets non adjacents d'un polygone. En d'autres termes, les lignes diagonales commencent à un sommet de la figure et se retrouvent dans un autre qui n'est pas suivant.

Dans l'image ci-dessus, la diagonale d'un carré est indiquée en trait noir, qui peut être vu, rejoint deux coins opposés.

Les diagonales du carré mesurent de la même manière, mais dans le losange, leurs deux diagonales sont différentes, il y a une plus grande, plus longue et plus courte, plus courte.

Comment calculer le nombre diagonal d'un polygone?

La détermination du nombre de diagonales d'un polygone peut être simple lorsqu'il s'agit d'un carré ou d'un losange, mais à mesure que le nombre de côtés d'une figure augmente, il devient plus compliqué pour visualiser combien de diagonales il a.

C'est pourquoi une formule simple qui rendra ce processus beaucoup plus efficace est utilisée en mathématiques:

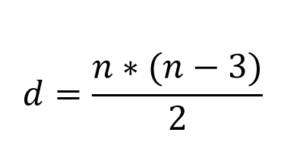
Il faut se rappeler que n est égal au nombre de côtés du polygone, et n doit toujours être supérieur à 3. Parce que? (Continuez à lire, la réponse est à la fin).

Exemple 1

Calculez la quantité de diagonales d'un octogone.

L'octogone est un polygone régulier à huit faces, cela signifie que tous ses côtés et angles internes sont les mêmes.

En utilisant la formule précédente, il suffit de remplacer n pour huit:

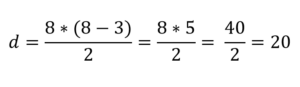
De cette façon, il est connu que le nombre de diagonales qui peuvent être tirés des sommets d'un polygone octogone est de 20.

Il peut vous servir: médias pondérés: comment il est calculé, exemples et exercices

Sans la formule, il est probablement lourd d'essayer de compter toutes les diagonales, même en ayant un bon dessin. Et plus la quantité de côtés sur la figure est élevée, plus elle sera compliquée.

Exemple 2

Calculez la longueur de la diagonale d'un rectangle avec le théorème de Pythagora.

Le théorème de Pythagore affirme que la somme des carrés des catégories d'un triangle rectangle, appelé a et b, est égale au carré de l'hypoténuse (le côté opposé à l'angle droit), appelé c.

En notation algébrique, ce serait:

pour² + b² = C²

La diagonale d'un rectangle forme un triangle rectangle, qui peut utiliser ce théorème, où b est la base et h est la hauteur.

Si la base est de 12 cm et que la hauteur est de 7 cm, lors du remplacement, c'est:

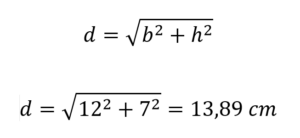
Par conséquent, la longueur de la diagonale dudit rectangle est de 13,89 centimètres.

Un polygone sans diagonales

Est-il possible qu'il existe un polygone qui n'a pas de lignes diagonales? Comment il serait?

Cette énigme peut être utilisée pour tirer la curiosité chez les enfants et les faire visualiser les diagonales d'une figure:

Le triangle est un polygone à trois faces et qui a trois angles internes. Mais il n'a pas de diagonale

Oui, le triangle n'a pas de diagonale.

Explication

Le triangle est un polygone à trois faces qui a trois angles internes. Mais les triangles sont des figures convexes qui n'ont pas de lignes diagonales, étant les polygones des mathématiques les plus simples et les plus fascinants.

Regarder bien la formule qui vous permet de calculer les diagonales d'un polygone:

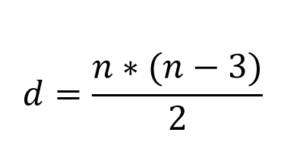
Il est immédiatement noté qu'en remplaçant n = 3, il est obtenu en conséquence d = 0. C'est-à-dire que les triangles n'ont pas de diagonales, il n'y a aucun moyen de dessiner un. Mais les polygones avec n = 4, par exemple, ont les deux diagonales.

Peut vous servir: Decagon: Propriétés régulières, irrégulières, exemples