Système de coordonnées rectangulaires

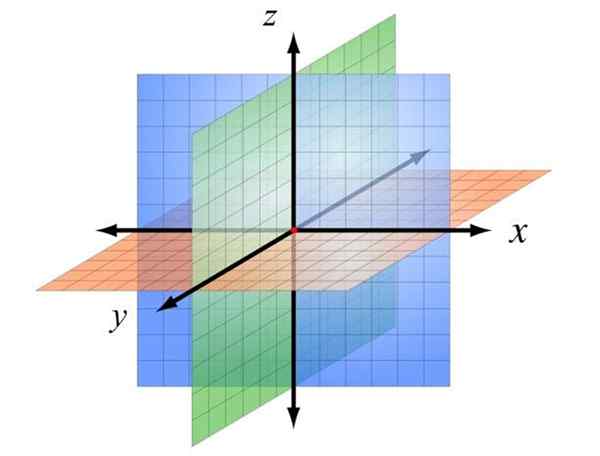
Système de coordonnées cartésiennes en trois dimensions. Source: Wikimedia Commons

Quel est le système de coordonnées rectangulaires?

En mathématiques et en géométrie, un système de coordonnées rectangulaires Il sert à localiser avec précision n'importe quel point sur l'espace. Pour cela, il suffit de donner trois coordonnées.

La construction du système dans le plan est très simple, seules trois lignes qui seront les axes de coordonnées ou les axes cartésiens sont nécessaires: une verticale, un autre horizontal et un tiers qui entre ou quitte le papier ou l'écran.

Ces axes sont mutuellement perpendiculaires et le point d'intersection est le Origine du système.

Cette disposition est indiquée dans la figure ci-dessus, dans laquelle les lettres ont été affectées aux lettres X, et, z, pour les distinguer. De cette façon, trois plans sont déterminés, avec l'origine colorée en rouge.

Le plan Xz, En bleu, c'est le plan de l'écran et se trouve devant les yeux du lecteur. Le plan Xy Il est orange et peut être associé à la table ou au sol. Enfin, l'avion zy En vert, il est perpendiculaire aux précédents et se coupez l'écran ou le papier dans deux régions.

Quadriculant chacun de ces plans et attribuant une échelle, vous pouvez placer n'importe quel point dans l'espace donnant les coordonnées respectives X y Z, Toujours dans cet ordre, pour éviter les ambiguïtés.

Pour quelle raisonIl sert le système de coordonnées rectangulaires?

Le système de coordonnées rectangulaires sert à positionner n'importe quel point dans l'espace ou dans le plan, suffisant pour indiquer les trois coordonnées du point, dans l'ordre x, y, z.

Il peut vous servir: variable nominale: concept et exemples

Si le point appartient à un avion, l'une des coordonnées sera 0 et si elle est sur l'un des axes, deux des coordonnées seront 0, sauf ce qui correspond à l'emplacement du point, sauf l'origine, qui, comme dit auparavant, a des coordonnées (0,0,0).

Les exemples suivants clarifient ce qui précède.

Exemples

Exemple 1

Un point p sur l'axe x est exprimé par coordonnées p (x, 0, 0). Notez que l'origine, mise en évidence en rouge dans la figure suivante, a des coordonnées ou (0, 0, 0).

Lorsque le point est à droite de l'origine, il a une coordonnée X positive, alors que s'il est à gauche, c'est négatif. Par exemple, P1 Blue Point a des coordonnées (6,0,0), tandis que le point P2 en vert, a des coordonnées (-9,0,0).

Exemple 2

Dans la figure suivante, il y a deux axes, étant le Axe x l'axe horizontal et le Axe y La verticale. Avec cela, il suffit de représenter des points dans l'avion, deux coordonnées étant nécessaires. L'origine ou est le point (0,0).

Notez que la disposition des axes divise le plan en quatre régions appelées quadrants. Les axes au-dessus et à droite de l'origine sont désignés avec un signe positif, tandis que en dessous et à gauche, ils se distinguent avec un signe négatif.

Ensuite, les points dont les coordonnées sont positifs, correspondent au premier quadrant ou quadrant i. Le point vert a des coordonnées (2,3) et se trouve dans le quadrant i.

Pour sa part, le Red Point a des coordonnées (-3,1) et se trouve dans le quadrant II, tandis que les coordonnées du point bleu sont (-1.5; -2.5) Et c'est dans le quadrant III.

Peut vous servir: Factorisation commune: exemples et exercices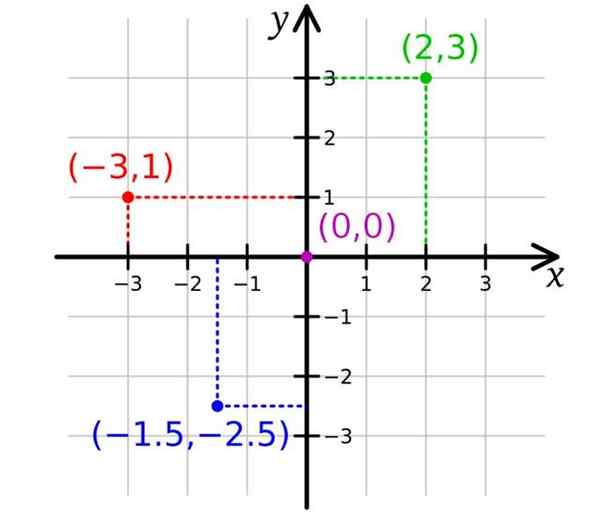 Plan cartésien. Source: Wikimedia Commons

Exemple 3

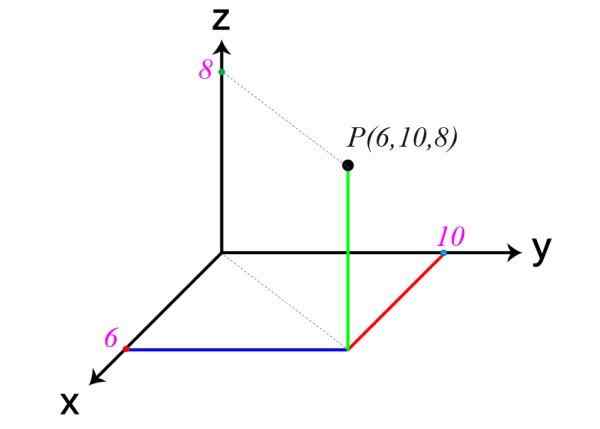
Ce qui suit est un exemple de point dans l'espace. Ses coordonnées sont x = 6, y = 10 et z = 8, donc p (6,10,8).

Un autre exemple de haches cartésiennes

Dans la figure du début, il est averti que les plans XY, XZ et ZY divisent l'espace en huit régions, appelées Octaveuse. Le point P de l'exemple est dans le premier ocant.

Les références

1. Alexander, D. (2013). Géométrie. 5e. Édition. Cengage Learning.
2. Larson, R. (2012). Précalation. 8e. Édition. Cengage Learning.
3. Stewart, J. (2007). Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
4. L'avion cartésien. Récupéré de: DL.UNCW.Édu.
5. Weisstein, E. Coordonnées cartésiennes. Récupéré de: Mathworld.Wolfram.com