Segment droit et semi-repris

Une ligne de ligne et un semi-droit se différencient dans le fait que le segment de ligne est limité; c'est-à-dire que leur point initial et leur point final sont connus. Du semi-droit est connu son point initial, mais pas son point final, car il s'étend à l'infini.

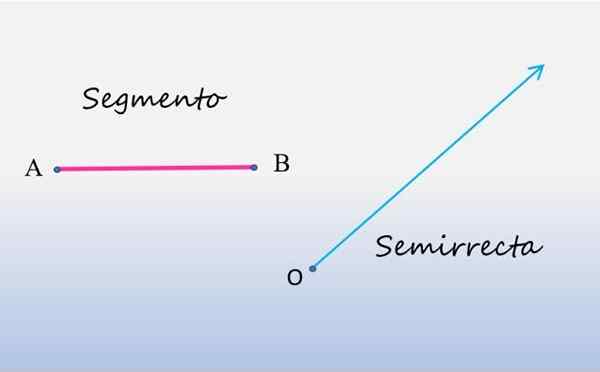
La figure suivante montre, à gauche, un segment de ligne et à droite, un semi-droit:

Segment et semi-droit. Source: F. Zapata.

Comme on peut le voir, le segment est une ligne de ligne, qui commence au point A et se termine au point B, ces points étant les fins dudit segment. La mesure du segment correspond à la longueur entre ses extrémités.

Pour sa part, le semi-droit a son point de départ au point O et s'étend à l'infini, ce qui équivaut à dire qu'il n'est limité qu'à une extrémité, généralement appelée origine. Pour cette raison, ils sont également appelés Bonté divine.

Les segments sont indiqués à travers les lettres qui indiquent le point initial et la fin. Par exemple, le segment de la figure est le segment AB, ou une course est placée sur le dessus, comme ceci:

D'un autre côté, un semi-recouvre peut également être nommé avec deux lettres, une indiquant le point correspondant à l'origine et une autre lettre supplémentaire. Il peut également être utilisé une minuscule lettre pour représenter la foudre ou la semi-décréation, et il y a aussi semi-sort avec son propre nom, comme nous le verrons dans les exemples plus tard.

Exemples de segments

Les segments sont très importants en géométrie, ci-dessous sont parmi les plus notables:

Côtés d'un polygone

Les polygones sont des figures plates et fermées, dont les côtés sont des segments de ligne non consécutifs. Par exemple, un triangle a trois côtés, un quadrilatère a quatre côtés, un pentagone en a cinq et ainsi de suite.

Il peut vous servir: Tesseldos: caractéristique, types (réguliers, irréguliers), exemples

Diamètre d'une circonférence

Il est défini comme ce segment qui contient deux points de circonférence et passe nécessairement par le centre de la même.

Corde d'une circonférence

Lorsqu'un segment qui rejoint deux points de circonférence ne passe pas par son centre, il est appelé corde.

Hauteur d'un triangle

La hauteur d'un triangle est définie comme le segment qui va perpendiculairement à l'un des côtés du triangle au sommet opposé. Si la mesure de la base d'un triangle, appelé B et la hauteur de la même, indiquée comme H est connue, la zone a de la même est calculée à travers la formule bien connue:

A = ½ b ∙ h

Exemples de semire

Les semi-sortants sont également des éléments très importants en géométrie. Certains semi-sortants bien connus sont:

Les semi-sessines positives

Les trois directions dans l'espace: élevée, large et profonde, peuvent être représentées par un système d'axes cartésiens, composé de trois lignes mutuellement perpendiculaires les unes avec les autres, désignées comme des axes X, et et z, qui sont coupés à un point appelé Origine.

Cette disposition divise l'espace en huit régions appelées Octaveuse. Dans la figure suivante, les semi-sadands positifs sont observés X, et et z, qui déterminent le premier ocant. De même, le semi -x positif déterminent la région du plan appelé Premier quadrant.

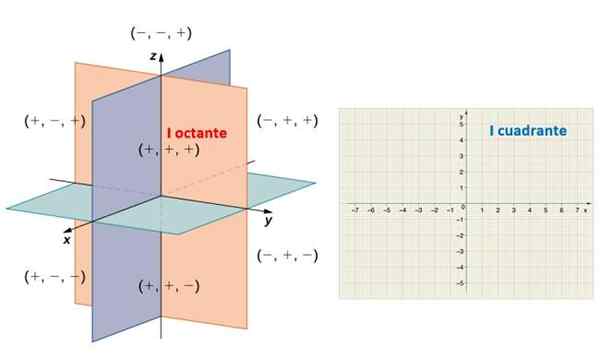À gauche, les huit octants de l'espace et à droite, le plan cartésien divisé en quatre quadrants. Source: Math Libreretsxts.

Les côtés d'un angle

Un angle est la fraction du plan délimité par deux semi-sortants dont l'origine est courante. Ce point en commun est le sommet de l'angle, tandis que la semi-sort est appelée, respectivement, côté initial et côté final de l'angle. Une telle disposition est indiquée dans la figure suivante:

Il peut vous servir: quelle est la relation entre la zone du losange et le rectangle?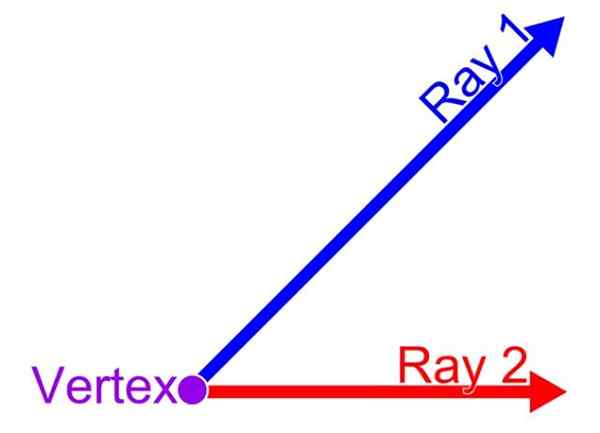 Éléments d'un angle. Source: Wikimedia Commons.