Réactance inductive

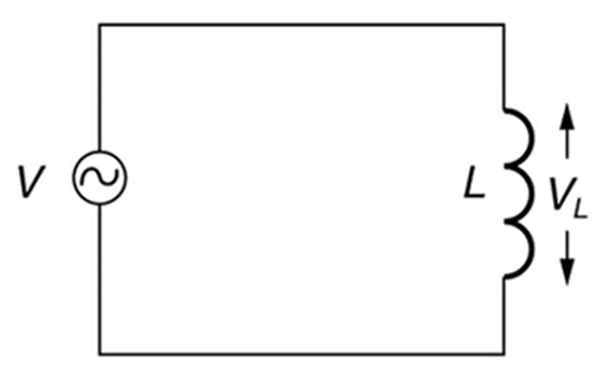
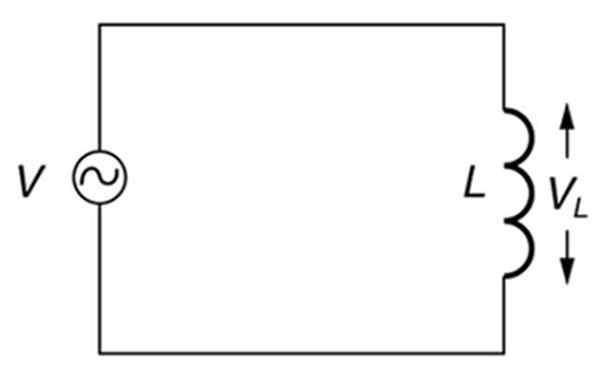Un circuit alternatif purement inductif. Source: Open Stax. Physique du collège.

Qu'est-ce que la réactance inductive?

La Réactance inductive Il se réfère à l'opposition présentée par la bobine au passage du courant, dans un circuit alternatif. En d'autres termes, c'est la capacité de l'inducteur à réduire le courant dans un autre circuit. Indiqué comme x_L, Sa valeur dépend de l'inductance et de la fréquence angulaire de la tension:

X_L= Ω ∙ L

Où ω est la fréquence angulaire dans les radians / s et l'inductance.

Les grandes inductances produisent une grande réactance inductive, car leur résistance au changement est plus élevée. Et la réactance augmente également avec la fréquence, donc une certaine inductance l produira une réactance plus grande, plus la fréquence de tension est élevée.

L'unité de réactance inductive est l'Ohmio, symbolisé par Ω. C'est la même unité de résistance électrique, mais contrairement à cela, x_L Il n'est pas constant, car cela dépend de la fréquence de la tension alternative appliquée.

Par conséquent, dans un circuit dont les seuls éléments sont une source alternative et une inductance (circuit inductif), comme celui montré dans la figure ci-dessus, la réactance inductive dépendra de la fréquence de la source.

Cependant, l'analogie de X_L Avec la résistance électrique, il peut être étendu au circuit inductif, permettant l'application de la loi d'Ohm. Si x est défini_L comme le rapport entre les amplitudes de tension V_L Dans l'inductance, et le courant i_L Cela le traverse:

X_L = V_L / Yo_L

Vous pouvez écrire la loi sur l'OHM pour les circuits purement inductifs comme suit:

V_L = X_L∙ I_L

Formules de réactance inductive

Pour calculer la réactance inductive, la formule donnée au début est utilisée, dans laquelle l représente l'inductance (Henrios) et ω est la fréquence angulaire (radians / seconde):

Peut vous servir: Expérience Millikan: procédure, explication, importance

X_L= Ω ∙ L

Il est courant que la fréquence soit exprimée dans Hertz ou Hertzio (Hz). Dans ce cas, il est désigné par F et est lié à la fréquence angulaire à travers la formule:

Ω = 2π ∙ f

Dans ce cas, la réactance est calculée comme suit:

X_L= 2πf ∙ l

Dans l'une de ces formules, la réactance inductive entraîne des ohms, comme expliqué précédemment.

L'effet de l'inductance sur un circuit inductif

Étant donné que l'inductance s'oppose aux changements ou variations du courant, la réactance inductive est caractérisée en retardant l'onde de courant par rapport à l'onde de tension.

Dans le graphique suivant, qui montre la tension V_L (Bleu) et le actuel i_L (rouge) Dans l'inductance, tous deux sinoïdes, il est observé que les deux vagues sont obsolètes à 90 °. À partir de t = 0, la valeur de tension est maximale, cependant, le courant est nul à ce moment.

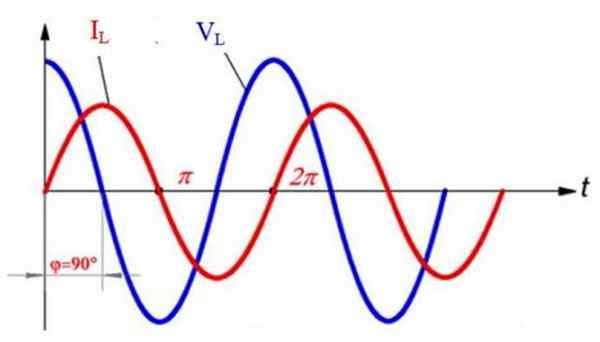Courant alternatif et tension dans un circuit inductif. Préparé par: f. Zapata.

Plus tard, il est observé que le courant atteint sa valeur maximale à t = π / 2, mais d'ici là, la tension est annulée et investit sa polarité, c'est-à-dire qu'elle devient négative. Simultanément, le courant diminue sa valeur, tandis que la tension devient de plus en plus négative.

Par la suite, à t = π, la tension atteint sa magnitude maximale, bien qu'avec la polarité inversée, puis le courant est annulé. De tout cela, il s'ensuit que chaque fois V_L Il atteint un pic, le courant est annulé, et chaque fois que le courant atteint sa magnitude maximale, la tension est 0.

Le courant atteint toujours son pic après la tension, et c'est parce que, comme indiqué au début, l'inductance s'oppose à l'augmentation ou diminue.

Peut vous servir: avantage mécanique: formule, équations, calcul et exemples

Comment calculer la réactance inductive

Le calcul de la réactance inductive est très simple: il est nécessaire de connaître la valeur de l'inductance et la fréquence de la tension alternative appliquée. Ensuite, ces données sont remplacées dans l'une des formules données dans la section précédente et l'opération correspondante est effectuée.

Les exemples suivants et les exercices résolus montrent comment le faire dans diverses situations.

Exemples

Exemple 1

Supposons une inductance l = 5 mh, à laquelle une autre tension de fréquence est appliquée 60.0 Hz. La réactance inductive dans ce cas est calculée par:

X_L= 2πf ∙ l

Mais avant de remplacer les valeurs, l'inductance doit devenir Henrios, en multipliant par le facteur 1 × 10⁻³. Donc:

L = 5 × 10⁻³ H

Ensuite:

X_L= 2πf ∙ l = x_L= 2π × 60 Hz × 5 × 10⁻³ H = 1. 88 ohm

Exemple 2

Maintenant, la même inductance est connectée à une autre tension de fréquence alternative: 10.0 kHz. Dans ce cas, l'inductance présente une plus grande réactance:

X_L= 2πf ∙ l = x_L= 2π × 10.0 × 10³ Hz × 5 × 10⁻³ H = 314.2 ohms

Exemple 3

La tension appliquée à l'inductance des exemples 1 et 2 a une valeur de 120 V RMS. Le courant RMS respectif est déterminé par la loi OHM V_L = X_L∙ I_L:

Toi_L = V_L / X_L

Pour la fréquence de 60.0 Hz, le courant est:

Toi_L = 120 v / 1. 88 ohm = 63.8 A

Et pour la fréquence de 10.0 kHz:

Toi_L = 120 v / 314.2 ohm = 0.38 A

Étant donné que dans ce dernier cas, la réactance est beaucoup plus grande, il est prévu que le courant soit plus petit. Cette propriété fait de l'inductance un filtre à haute fréquence, une fonctionnalité utilisée pour réduire les sons à haute fréquence dans l'équipement sonore, ou pour protéger les appareils des actuels soudains, entre autres applications.

Peut vous servir: Théorème de Steiner: explication, applications, exercices

Exercices résolus

Exercice 1

Déterminer la réactance inductive dans un circuit qui se compose d'une inductance de 2.5 MH, en série avec une autre source de tension, dont la fréquence est de 75 R.p.m.

Solution

Une révolution complète ou un cycle est égal à 2π radians, et une minute a 60 secondes, par conséquent, une fréquence de 75 R.p.M équivaut à:

75 R.p.M = 75 × 2π radians / 60 secondes = 7.85 radians / s

Et avec cette valeur, la réactance est:

X_L= Ω ∙ l = (7.85 radians / s) × 2.5 × 10⁻³ H = 0.02 Ω

Exercice 2

L'inductance en série est utilisée avec la source d'un ordinateur pour filtrer le bruit des hautes fréquences.

a) Quelle devrait être la valeur d'inductance minimale nécessaire pour produire une réactance de 2 kΩ, si la fréquence du signal qui est à filtrer est de 15 kHz?

b) Trouvez la réactance de cette inductance à la fréquence de 60 Hz.

Solution à

X_L = 2 kΩ = 2000 Ω

F = 15 kHz = 15000 Hz

Par conséquent, le nettoyage de l'équation x_L= 2πf ∙ l, vous avez:

L = x_L / 2π ∙ f = 2000 Ω / 2π × 15000 Hz = 0.0212 H = 21.2 MH

Solution B

En utilisant à nouveau x_L= 2πf ∙ l, mais avec f = 60 Hz, résultats:

X_L= 2π × 60 Hz × 0.0212 H = 8 ohm.

Les références

1. Bauer, w. (2011). Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill. 
2. Giancoli, D. (2006). Physique: principes avec applications. 6e. Ed Prentice Hall.
3.  Katz, D. (2013). Physique pour les scientifiques et les ingénieurs. Fondations et connexions. Cengage Learning.
4. Stax ouvert. Physique du collège. Récupéré de: OpenStax.org.
5. Sears, Z. (2016). Physique universitaire avec physique moderne. 14e. Élégant. 2ieme volume. Pearson